Guided Quantum Compression for Higgs Identification

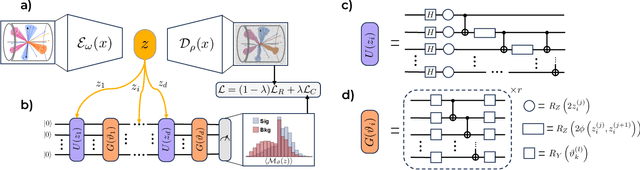
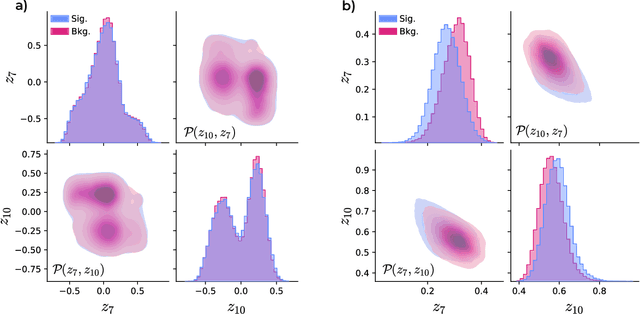
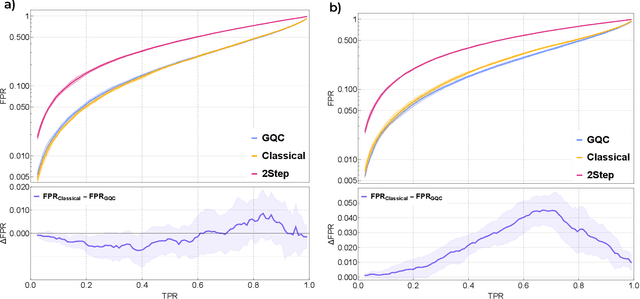
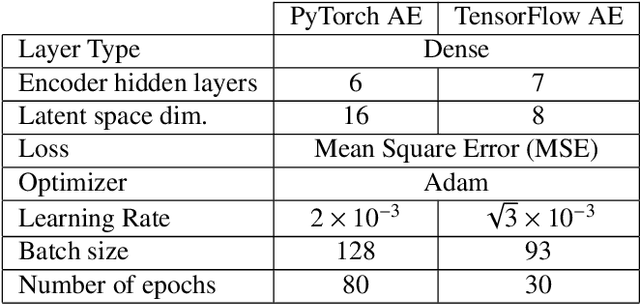
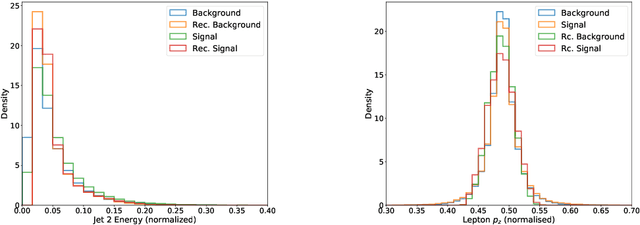
Quantum machine learning provides a fundamentally novel and promising approach to analyzing data. However, many data sets are too complex for currently available quantum computers. Consequently, quantum machine learning applications conventionally resort to dimensionality reduction algorithms, e.g., auto-encoders, before passing data through the quantum models. We show that using a classical auto-encoder as an independent preprocessing step can significantly decrease the classification performance of a quantum machine learning algorithm. To ameliorate this issue, we design an architecture that unifies the preprocessing and quantum classification algorithms into a single trainable model: the guided quantum compression model. The utility of this model is demonstrated by using it to identify the Higgs boson in proton-proton collisions at the LHC, where the conventional approach proves ineffective. Conversely, the guided quantum compression model excels at solving this classification problem, achieving a good accuracy. Additionally, the model developed herein shows better performance compared to the classical benchmark when using only low-level kinematic features.

Provable advantages of kernel-based quantum learners and quantum preprocessing based on Grover's algorithm

There is an ongoing effort to find quantum speedups for learning problems. Recently, [Y. Liu et al., Nat. Phys. $\textbf{17}$, 1013--1017 (2021)] have proven an exponential speedup for quantum support vector machines by leveraging the speedup of Shor's algorithm. We expand upon this result and identify a speedup utilizing Grover's algorithm in the kernel of a support vector machine. To show the practicality of the kernel structure we apply it to a problem related to pattern matching, providing a practical yet provable advantage. Moreover, we show that combining quantum computation in a preprocessing step with classical methods for classification further improves classifier performance.

Quantum anomaly detection in the latent space of proton collision events at the LHC

We propose a new strategy for anomaly detection at the LHC based on unsupervised quantum machine learning algorithms. To accommodate the constraints on the problem size dictated by the limitations of current quantum hardware we develop a classical convolutional autoencoder. The designed quantum anomaly detection models, namely an unsupervised kernel machine and two clustering algorithms, are trained to find new-physics events in the latent representation of LHC data produced by the autoencoder. The performance of the quantum algorithms is benchmarked against classical counterparts on different new-physics scenarios and its dependence on the dimensionality of the latent space and the size of the training dataset is studied. For kernel-based anomaly detection, we identify a regime where the quantum model significantly outperforms its classical counterpart. An instance of the kernel machine is implemented on a quantum computer to verify its suitability for available hardware. We demonstrate that the observed consistent performance advantage is related to the inherent quantum properties of the circuit used.

Higgs analysis with quantum classifiers

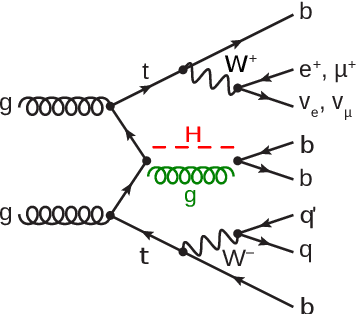
We have developed two quantum classifier models for the $t\bar{t}H(b\bar{b})$ classification problem, both of which fall into the category of hybrid quantum-classical algorithms for Noisy Intermediate Scale Quantum devices (NISQ). Our results, along with other studies, serve as a proof of concept that Quantum Machine Learning (QML) methods can have similar or better performance, in specific cases of low number of training samples, with respect to conventional ML methods even with a limited number of qubits available in current hardware. To utilise algorithms with a low number of qubits -- to accommodate for limitations in both simulation hardware and real quantum hardware -- we investigated different feature reduction methods. Their impact on the performance of both the classical and quantum models was assessed. We addressed different implementations of two QML models, representative of the two main approaches to supervised quantum machine learning today: a Quantum Support Vector Machine (QSVM), a kernel-based method, and a Variational Quantum Circuit (VQC), a variational approach.