Symmetry breaking in geometric quantum machine learning in the presence of noise

Geometric quantum machine learning based on equivariant quantum neural networks (EQNN) recently appeared as a promising direction in quantum machine learning. Despite the encouraging progress, the studies are still limited to theory, and the role of hardware noise in EQNN training has never been explored. This work studies the behavior of EQNN models in the presence of noise. We show that certain EQNN models can preserve equivariance under Pauli channels, while this is not possible under the amplitude damping channel. We claim that the symmetry breaking grows linearly in the number of layers and noise strength. We support our claims with numerical data from simulations as well as hardware up to 64 qubits. Furthermore, we provide strategies to enhance the symmetry protection of EQNN models in the presence of noise.

Approximately Equivariant Quantum Neural Network for $p4m$ Group Symmetries in Images

Quantum Neural Networks (QNNs) are suggested as one of the quantum algorithms which can be efficiently simulated with a low depth on near-term quantum hardware in the presence of noises. However, their performance highly relies on choosing the most suitable architecture of Variational Quantum Algorithms (VQAs), and the problem-agnostic models often suffer issues regarding trainability and generalization power. As a solution, the most recent works explore Geometric Quantum Machine Learning (GQML) using QNNs equivariant with respect to the underlying symmetry of the dataset. GQML adds an inductive bias to the model by incorporating the prior knowledge on the given dataset and leads to enhancing the optimization performance while constraining the search space. This work proposes equivariant Quantum Convolutional Neural Networks (EquivQCNNs) for image classification under planar $p4m$ symmetry, including reflectional and $90^\circ$ rotational symmetry. We present the results tested in different use cases, such as phase detection of the 2D Ising model and classification of the extended MNIST dataset, and compare them with those obtained with the non-equivariant model, proving that the equivariance fosters better generalization of the model.

Running the Dual-PQC GAN on noisy simulators and real quantum hardware

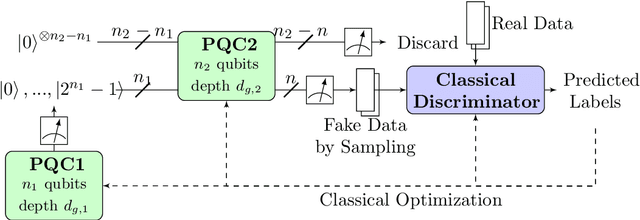
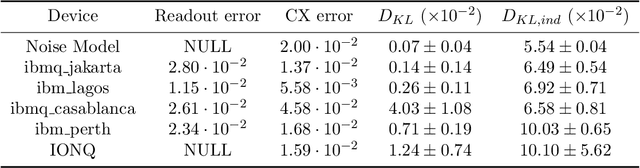
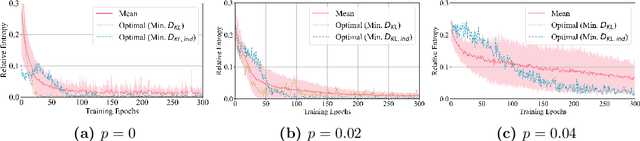
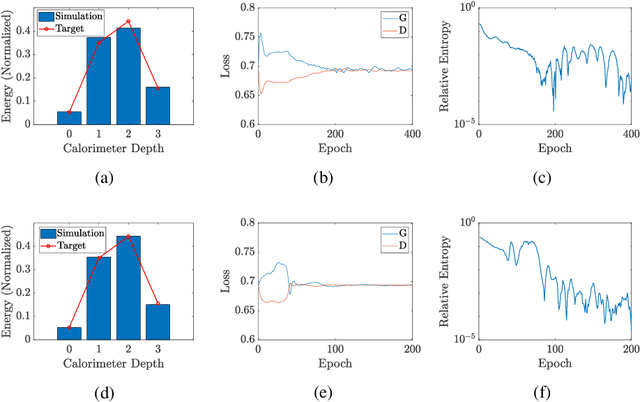
In an earlier work, we introduced dual-Parameterized Quantum Circuit (PQC) Generative Adversarial Networks (GAN), an advanced prototype of a quantum GAN. We applied the model on a realistic High-Energy Physics (HEP) use case: the exact theoretical simulation of a calorimeter response with a reduced problem size. This paper explores the dual- PQC GAN for a more practical usage by testing its performance in the presence of different types of quantum noise, which are the major obstacles to overcome for successful deployment using near-term quantum devices. The results propose the possibility of running the model on current real hardware, but improvements are still required in some areas.

Dual-Parameterized Quantum Circuit GAN Model in High Energy Physics

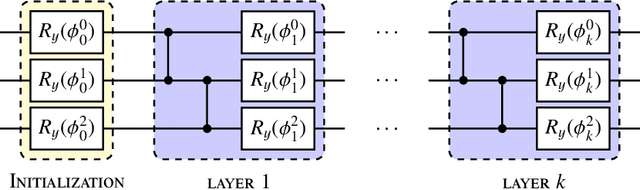
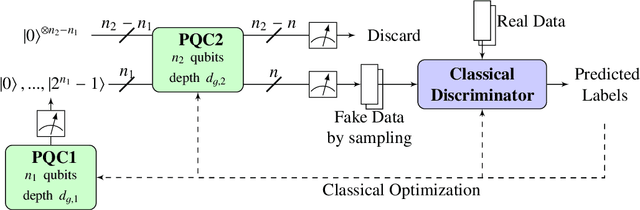
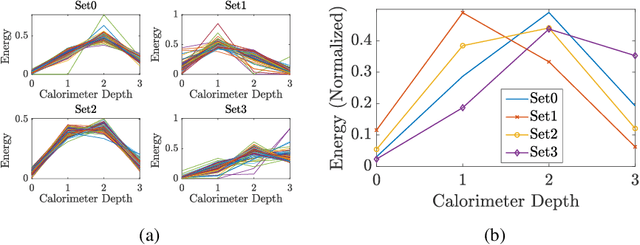
Generative models, and Generative Adversarial Networks (GAN) in particular, are being studied as possible alternatives to Monte Carlo simulations. It has been proposed that, in certain circumstances, simulation using GANs can be sped-up by using quantum GANs (qGANs). We present a new design of qGAN, the dual-Parameterized Quantum Circuit(PQC) GAN, which consists of a classical discriminator and two quantum generators which take the form of PQCs. The first PQC learns a probability distribution over N-pixel images, while the second generates normalized pixel intensities of an individual image for each PQC input. With a view to HEP applications, we evaluated the dual-PQC architecture on the task of imitating calorimeter outputs, translated into pixelated images. The results demonstrate that the model can reproduce a fixed number of images with a reduced size as well as their probability distribution and we anticipate it should allow us to scale up to real calorimeter outputs.

Quantum Generative Adversarial Networks in a Continuous-Variable Architecture to Simulate High Energy Physics Detectors

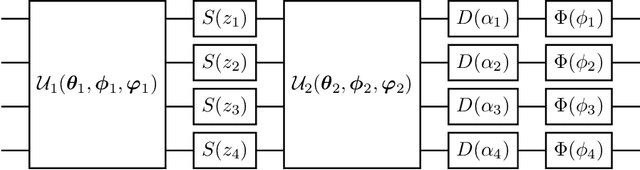
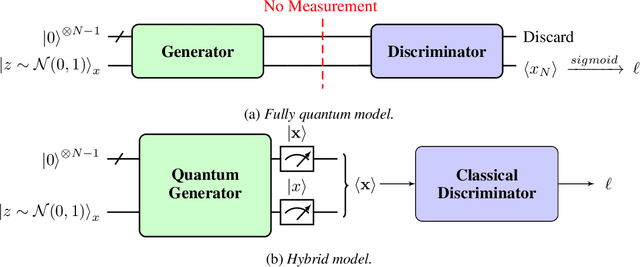
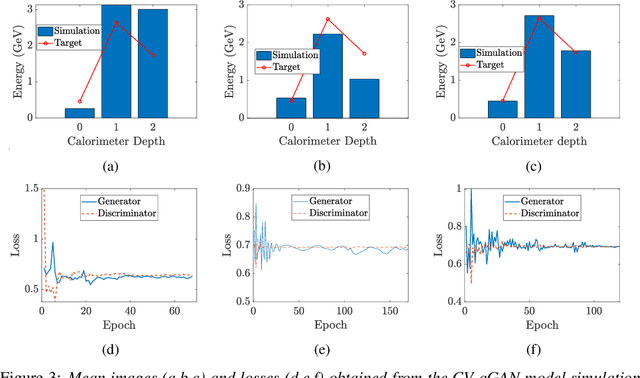
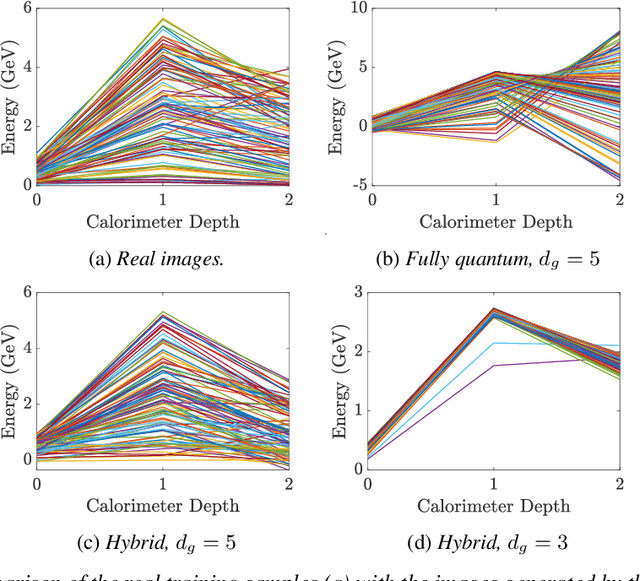
Deep Neural Networks (DNNs) come into the limelight in High Energy Physics (HEP) in order to manipulate the increasing amount of data encountered in the next generation of accelerators. Recently, the HEP community has suggested Generative Adversarial Networks (GANs) to replace traditional time-consuming Geant4 simulations based on the Monte Carlo method. In parallel with advances in deep learning, intriguing studies have been conducted in the last decade on quantum computing, including the Quantum GAN model suggested by IBM. However, this model is limited in learning a probability distribution over discrete variables, while we initially aim to reproduce a distribution over continuous variables in HEP. We introduce and analyze a new prototype of quantum GAN (qGAN) employed in continuous-variable (CV) quantum computing, which encodes quantum information in a continuous physical observable. Two CV qGAN models with a quantum and a classical discriminator have been tested to reproduce calorimeter outputs in a reduced size, and their advantages and limitations are discussed.