Symmetry breaking in geometric quantum machine learning in the presence of noise

Geometric quantum machine learning based on equivariant quantum neural networks (EQNN) recently appeared as a promising direction in quantum machine learning. Despite the encouraging progress, the studies are still limited to theory, and the role of hardware noise in EQNN training has never been explored. This work studies the behavior of EQNN models in the presence of noise. We show that certain EQNN models can preserve equivariance under Pauli channels, while this is not possible under the amplitude damping channel. We claim that the symmetry breaking grows linearly in the number of layers and noise strength. We support our claims with numerical data from simulations as well as hardware up to 64 qubits. Furthermore, we provide strategies to enhance the symmetry protection of EQNN models in the presence of noise.

Quantum encoding is suitable for matched filtering

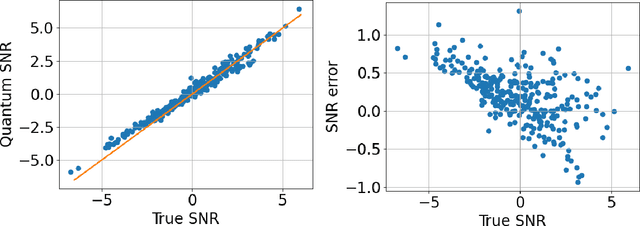
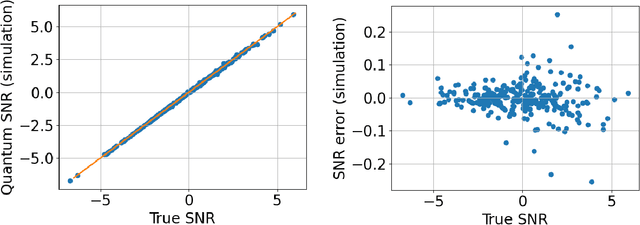
Matched filtering is a powerful signal searching technique used in several employments from radar and communications applications to gravitational-wave detection. Here we devise a method for matched filtering with the use of quantum bits. Our method's asymptotic time complexity does not depend on template length and, including encoding, is $\mathcal{O}(L(\log_2L)^2)$ for a data with length $L$ and a template with length $N$, which is classically $\mathcal{O}(NL)$. Hence our method has superior time complexity over the classical computation for long templates. We demonstrate our method with real quantum hardware on 4 qubits and also with simulations.

Hybrid Quantum Classical Graph Neural Networks for Particle Track Reconstruction

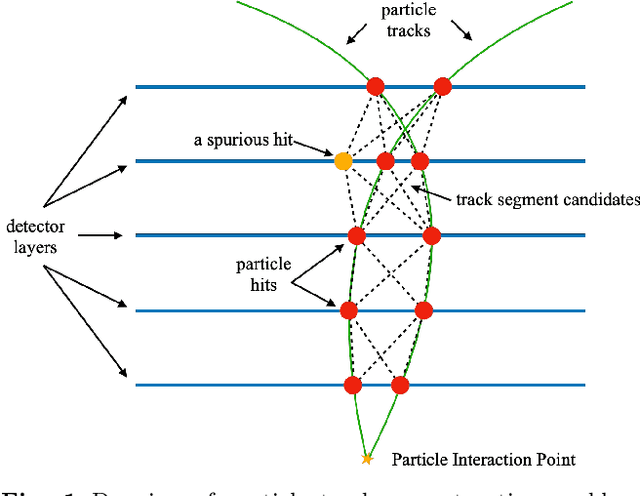
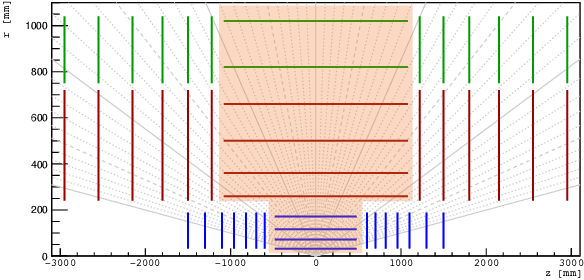
The Large Hadron Collider (LHC) at the European Organisation for Nuclear Research (CERN) will be upgraded to further increase the instantaneous rate of particle collisions (luminosity) and become the High Luminosity LHC (HL-LHC). This increase in luminosity will significantly increase the number of particles interacting with the detector. The interaction of particles with a detector is referred to as "hit". The HL-LHC will yield many more detector hits, which will pose a combinatorial challenge by using reconstruction algorithms to determine particle trajectories from those hits. This work explores the possibility of converting a novel Graph Neural Network model, that can optimally take into account the sparse nature of the tracking detector data and their complex geometry, to a Hybrid Quantum-Classical Graph Neural Network that benefits from using Variational Quantum layers. We show that this hybrid model can perform similar to the classical approach. Also, we explore Parametrized Quantum Circuits (PQC) with different expressibility and entangling capacities, and compare their training performance in order to quantify the expected benefits. These results can be used to build a future road map to further develop circuit based Hybrid Quantum-Classical Graph Neural Networks.