Dual-Parameterized Quantum Circuit GAN Model in High Energy Physics

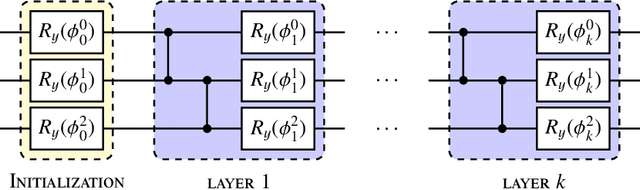
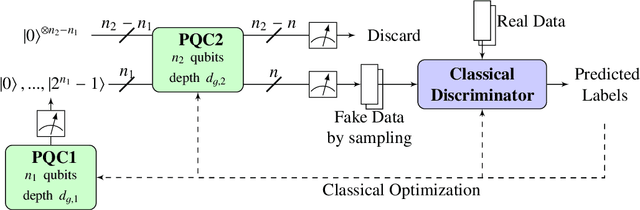
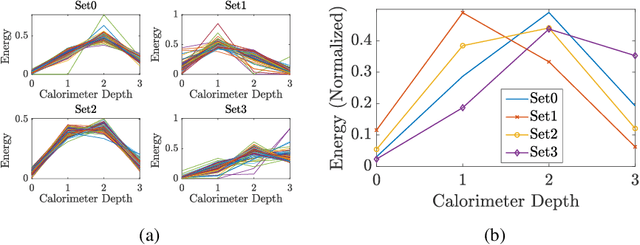
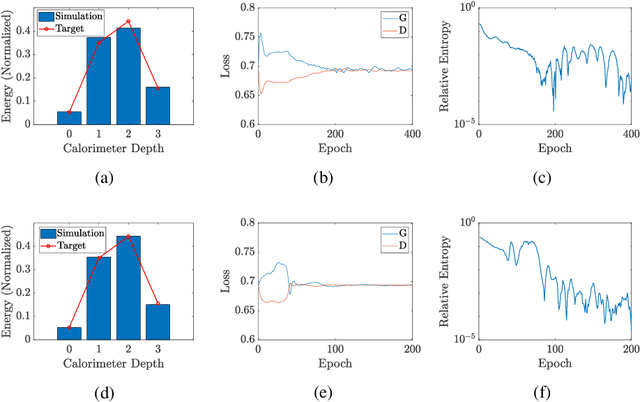
Generative models, and Generative Adversarial Networks (GAN) in particular, are being studied as possible alternatives to Monte Carlo simulations. It has been proposed that, in certain circumstances, simulation using GANs can be sped-up by using quantum GANs (qGANs). We present a new design of qGAN, the dual-Parameterized Quantum Circuit(PQC) GAN, which consists of a classical discriminator and two quantum generators which take the form of PQCs. The first PQC learns a probability distribution over N-pixel images, while the second generates normalized pixel intensities of an individual image for each PQC input. With a view to HEP applications, we evaluated the dual-PQC architecture on the task of imitating calorimeter outputs, translated into pixelated images. The results demonstrate that the model can reproduce a fixed number of images with a reduced size as well as their probability distribution and we anticipate it should allow us to scale up to real calorimeter outputs.

Optimising Clifford Circuits with Quantomatic

We present a system of equations between Clifford circuits, all derivable in the ZX-calculus, and formalised as rewrite rules in the Quantomatic proof assistant. By combining these rules with some non-trivial simplification procedures defined in the Quantomatic tactic language, we demonstrate the use of Quantomatic as a circuit optimisation tool. We prove that the system always reduces Clifford circuits of one or two qubits to their minimal form, and give numerical results demonstrating its performance on larger Clifford circuits.

Verifying the Steane code with Quantomatic

In this paper we give a partially mechanized proof of the correctness of Steane's 7-qubit error correcting code, using the tool Quantomatic. To the best of our knowledge, this represents the largest and most complicated verification task yet carried out using Quantomatic.

Graphical Reasoning in Compact Closed Categories for Quantum Computation

Compact closed categories provide a foundational formalism for a variety of important domains, including quantum computation. These categories have a natural visualisation as a form of graphs. We present a formalism for equational reasoning about such graphs and develop this into a generic proof system with a fixed logical kernel for equational reasoning about compact closed categories. Automating this reasoning process is motivated by the slow and error prone nature of manual graph manipulation. A salient feature of our system is that it provides a formal and declarative account of derived results that can include `ellipses'-style notation. We illustrate the framework by instantiating it for a graphical language of quantum computation and show how this can be used to perform symbolic computation.