Double descent in quantum machine learning

The double descent phenomenon challenges traditional statistical learning theory by revealing scenarios where larger models do not necessarily lead to reduced performance on unseen data. While this counterintuitive behavior has been observed in a variety of classical machine learning models, particularly modern neural network architectures, it remains elusive within the context of quantum machine learning. In this work, we analytically demonstrate that quantum learning models can exhibit double descent behavior by drawing on insights from linear regression and random matrix theory. Additionally, our numerical experiments on quantum kernel methods across different real-world datasets and system sizes further confirm the existence of a test error peak, a characteristic feature of double descent. Our findings provide evidence that quantum models can operate in the modern, overparameterized regime without experiencing overfitting, thereby opening pathways to improved learning performance beyond traditional statistical learning theory.

Does provable absence of barren plateaus imply classical simulability? Or, why we need to rethink variational quantum computing

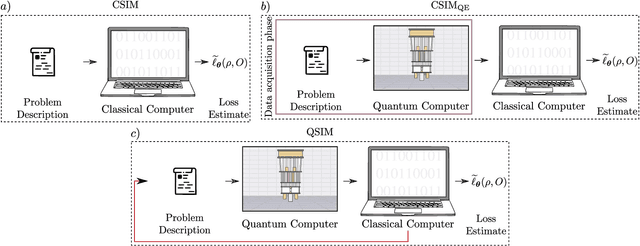
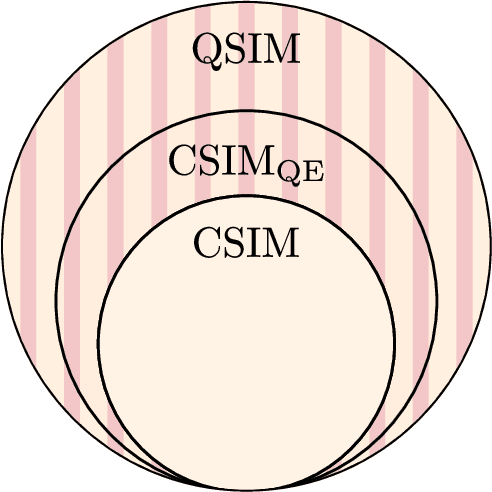
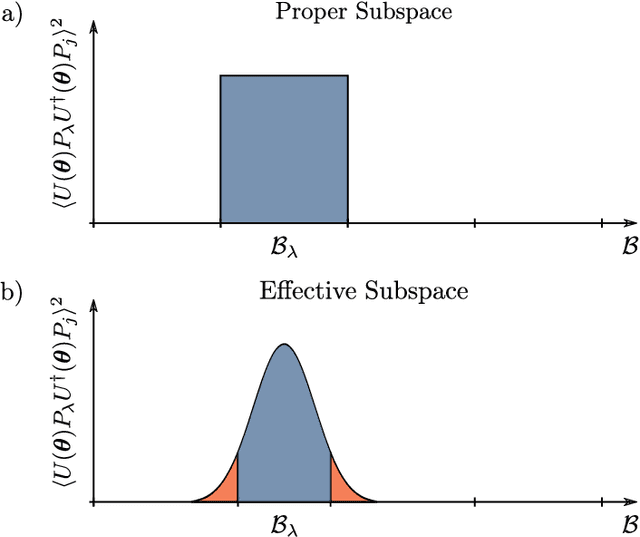
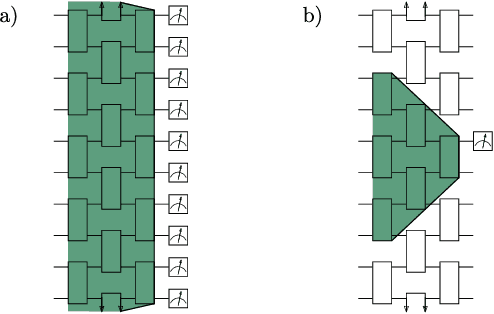
A large amount of effort has recently been put into understanding the barren plateau phenomenon. In this perspective article, we face the increasingly loud elephant in the room and ask a question that has been hinted at by many but not explicitly addressed: Can the structure that allows one to avoid barren plateaus also be leveraged to efficiently simulate the loss classically? We present strong evidence that commonly used models with provable absence of barren plateaus are also classically simulable, provided that one can collect some classical data from quantum devices during an initial data acquisition phase. This follows from the observation that barren plateaus result from a curse of dimensionality, and that current approaches for solving them end up encoding the problem into some small, classically simulable, subspaces. This sheds serious doubt on the non-classicality of the information processing capabilities of parametrized quantum circuits for barren plateau-free landscapes and on the possibility of superpolynomial advantages from running them on quantum hardware. We end by discussing caveats in our arguments, the role of smart initializations, and by highlighting new opportunities that our perspective raises.