Detecting underdetermination in parameterized quantum circuits

A central question in machine learning is how reliable the predictions of a trained model are. Reliability includes the identification of instances for which a model is likely not to be trusted based on an analysis of the learning system itself. Such unreliability for an input may arise from the model family providing a variety of hypotheses consistent with the training data, which can vastly disagree in their predictions on that particular input point. This is called the underdetermination problem, and it is important to develop methods to detect it. With the emergence of quantum machine learning (QML) as a prospective alternative to classical methods for certain learning problems, the question arises to what extent they are subject to underdetermination and whether similar techniques as those developed for classical models can be employed for its detection. In this work, we first provide an overview of concepts from Safe AI and reliability, which in particular received little attention in QML. We then explore the use of a method based on local second-order information for the detection of underdetermination in parameterized quantum circuits through numerical experiments. We further demonstrate that the approach is robust to certain levels of shot noise. Our work contributes to the body of literature on Safe Quantum AI, which is an emerging field of growing importance.

Double descent in quantum machine learning

The double descent phenomenon challenges traditional statistical learning theory by revealing scenarios where larger models do not necessarily lead to reduced performance on unseen data. While this counterintuitive behavior has been observed in a variety of classical machine learning models, particularly modern neural network architectures, it remains elusive within the context of quantum machine learning. In this work, we analytically demonstrate that quantum learning models can exhibit double descent behavior by drawing on insights from linear regression and random matrix theory. Additionally, our numerical experiments on quantum kernel methods across different real-world datasets and system sizes further confirm the existence of a test error peak, a characteristic feature of double descent. Our findings provide evidence that quantum models can operate in the modern, overparameterized regime without experiencing overfitting, thereby opening pathways to improved learning performance beyond traditional statistical learning theory.

Quadratic Advantage with Quantum Randomized Smoothing Applied to Time-Series Analysis

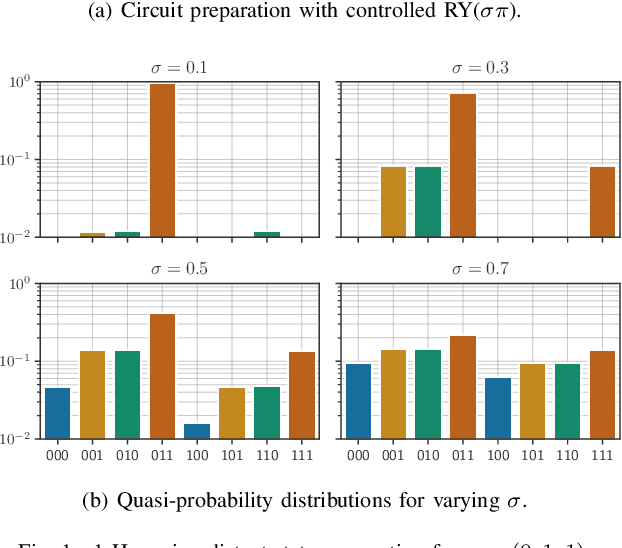
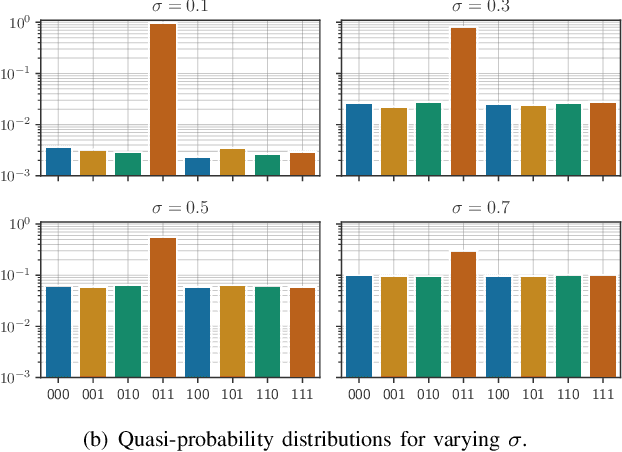
As quantum machine learning continues to develop at a rapid pace, the importance of ensuring the robustness and efficiency of quantum algorithms cannot be overstated. Our research presents an analysis of quantum randomized smoothing, how data encoding and perturbation modeling approaches can be matched to achieve meaningful robustness certificates. By utilizing an innovative approach integrating Grover's algorithm, a quadratic sampling advantage over classical randomized smoothing is achieved. This strategy necessitates a basis state encoding, thus restricting the space of meaningful perturbations. We show how constrained $k$-distant Hamming weight perturbations are a suitable noise distribution here, and elucidate how they can be constructed on a quantum computer. The efficacy of the proposed framework is demonstrated on a time series classification task employing a Bag-of-Words pre-processing solution. The advantage of quadratic sample reduction is recovered especially in the regime with large number of samples. This may allow quantum computers to efficiently scale randomized smoothing to more complex tasks beyond the reach of classical methods.