Detecting underdetermination in parameterized quantum circuits

A central question in machine learning is how reliable the predictions of a trained model are. Reliability includes the identification of instances for which a model is likely not to be trusted based on an analysis of the learning system itself. Such unreliability for an input may arise from the model family providing a variety of hypotheses consistent with the training data, which can vastly disagree in their predictions on that particular input point. This is called the underdetermination problem, and it is important to develop methods to detect it. With the emergence of quantum machine learning (QML) as a prospective alternative to classical methods for certain learning problems, the question arises to what extent they are subject to underdetermination and whether similar techniques as those developed for classical models can be employed for its detection. In this work, we first provide an overview of concepts from Safe AI and reliability, which in particular received little attention in QML. We then explore the use of a method based on local second-order information for the detection of underdetermination in parameterized quantum circuits through numerical experiments. We further demonstrate that the approach is robust to certain levels of shot noise. Our work contributes to the body of literature on Safe Quantum AI, which is an emerging field of growing importance.

Double descent in quantum machine learning

The double descent phenomenon challenges traditional statistical learning theory by revealing scenarios where larger models do not necessarily lead to reduced performance on unseen data. While this counterintuitive behavior has been observed in a variety of classical machine learning models, particularly modern neural network architectures, it remains elusive within the context of quantum machine learning. In this work, we analytically demonstrate that quantum learning models can exhibit double descent behavior by drawing on insights from linear regression and random matrix theory. Additionally, our numerical experiments on quantum kernel methods across different real-world datasets and system sizes further confirm the existence of a test error peak, a characteristic feature of double descent. Our findings provide evidence that quantum models can operate in the modern, overparameterized regime without experiencing overfitting, thereby opening pathways to improved learning performance beyond traditional statistical learning theory.

Discovering emergent connections in quantum physics research via dynamic word embeddings

As the field of quantum physics evolves, researchers naturally form subgroups focusing on specialized problems. While this encourages in-depth exploration, it can limit the exchange of ideas across structurally similar problems in different subfields. To encourage cross-talk among these different specialized areas, data-driven approaches using machine learning have recently shown promise to uncover meaningful connections between research concepts, promoting cross-disciplinary innovation. Current state-of-the-art approaches represent concepts using knowledge graphs and frame the task as a link prediction problem, where connections between concepts are explicitly modeled. In this work, we introduce a novel approach based on dynamic word embeddings for concept combination prediction. Unlike knowledge graphs, our method captures implicit relationships between concepts, can be learned in a fully unsupervised manner, and encodes a broader spectrum of information. We demonstrate that this representation enables accurate predictions about the co-occurrence of concepts within research abstracts over time. To validate the effectiveness of our approach, we provide a comprehensive benchmark against existing methods and offer insights into the interpretability of these embeddings, particularly in the context of quantum physics research. Our findings suggest that this representation offers a more flexible and informative way of modeling conceptual relationships in scientific literature.

Explainable Representation Learning of Small Quantum States

Unsupervised machine learning models build an internal representation of their training data without the need for explicit human guidance or feature engineering. This learned representation provides insights into which features of the data are relevant for the task at hand. In the context of quantum physics, training models to describe quantum states without human intervention offers a promising approach to gaining insight into how machines represent complex quantum states. The ability to interpret the learned representation may offer a new perspective on non-trivial features of quantum systems and their efficient representation. We train a generative model on two-qubit density matrices generated by a parameterized quantum circuit. In a series of computational experiments, we investigate the learned representation of the model and its internal understanding of the data. We observe that the model learns an interpretable representation which relates the quantum states to their underlying entanglement characteristics. In particular, our results demonstrate that the latent representation of the model is directly correlated with the entanglement measure concurrence. The insights from this study represent proof of concept towards interpretable machine learning of quantum states. Our approach offers insight into how machines learn to represent small-scale quantum systems autonomously.

Learning Coulomb Diamonds in Large Quantum Dot Arrays

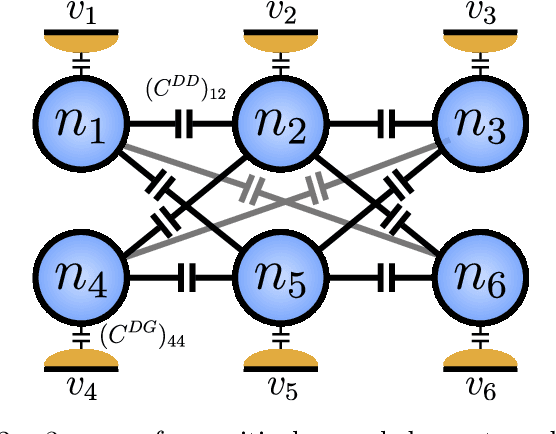
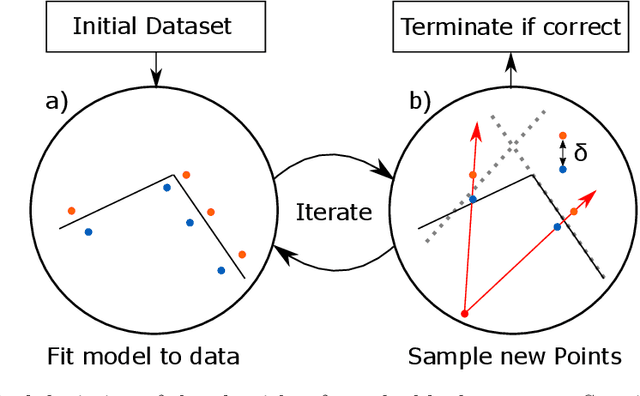
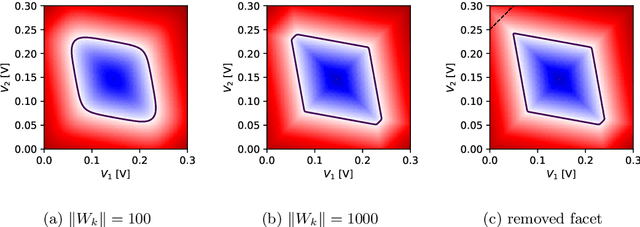
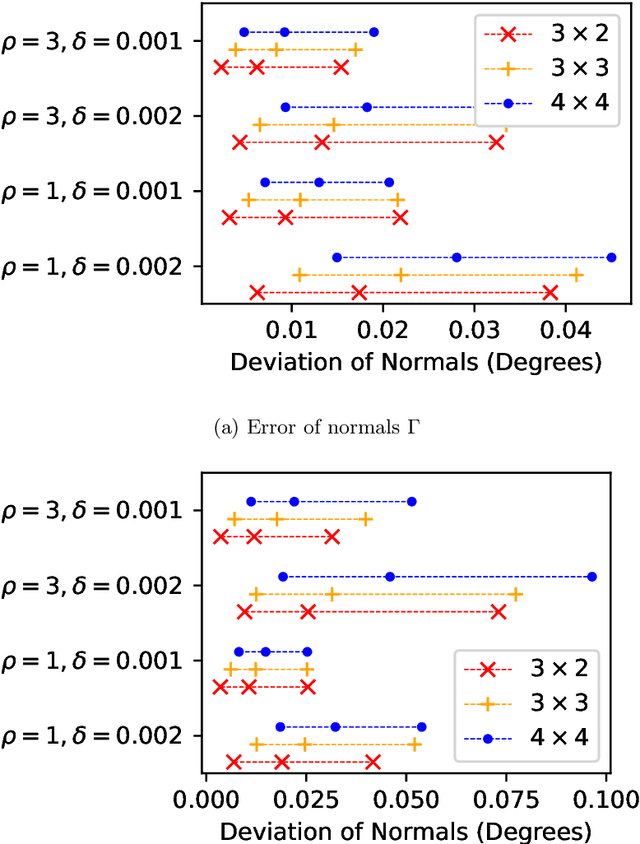
We introduce an algorithm that is able to find the facets of Coulomb diamonds in quantum dot arrays. We simulate these arrays using the constant-interaction model, and rely only on one-dimensional raster scans (rays) to learn a model of the device using regularized maximum likelihood estimation. This allows us to determine, for a given charge state of the device, which transitions exist and what the compensated gate voltages for these are. For smaller devices the simulator can also be used to compute the exact boundaries of the Coulomb diamonds, which we use to assess that our algorithm correctly finds the vast majority of transitions with high precision.