Opportunities and limitations of explaining quantum machine learning

A common trait of many machine learning models is that it is often difficult to understand and explain what caused the model to produce the given output. While the explainability of neural networks has been an active field of research in the last years, comparably little is known for quantum machine learning models. Despite a few recent works analyzing some specific aspects of explainability, as of now there is no clear big picture perspective as to what can be expected from quantum learning models in terms of explainability. In this work, we address this issue by identifying promising research avenues in this direction and lining out the expected future results. We additionally propose two explanation methods designed specifically for quantum machine learning models, as first of their kind to the best of our knowledge. Next to our pre-view of the field, we compare both existing and novel methods to explain the predictions of quantum learning models. By studying explainability in quantum machine learning, we can contribute to the sustainable development of the field, preventing trust issues in the future.

Concept learning of parameterized quantum models from limited measurements

Classical learning of the expectation values of observables for quantum states is a natural variant of learning quantum states or channels. While learning-theoretic frameworks establish the sample complexity and the number of measurement shots per sample required for learning such statistical quantities, the interplay between these two variables has not been adequately quantified before. In this work, we take the probabilistic nature of quantum measurements into account in classical modelling and discuss these quantities under a single unified learning framework. We provide provable guarantees for learning parameterized quantum models that also quantify the asymmetrical effects and interplay of the two variables on the performance of learning algorithms. These results show that while increasing the sample size enhances the learning performance of classical machines, even with single-shot estimates, the improvements from increasing measurements become asymptotically trivial beyond a constant factor. We further apply our framework and theoretical guarantees to study the impact of measurement noise on the classical surrogation of parameterized quantum circuit models. Our work provides new tools to analyse the operational influence of finite measurement noise in the classical learning of quantum systems.

On the relation between trainability and dequantization of variational quantum learning models

The quest for successful variational quantum machine learning (QML) relies on the design of suitable parametrized quantum circuits (PQCs), as analogues to neural networks in classical machine learning. Successful QML models must fulfill the properties of trainability and non-dequantization, among others. Recent works have highlighted an intricate interplay between trainability and dequantization of such models, which is still unresolved. In this work we contribute to this debate from the perspective of machine learning, proving a number of results identifying, among others when trainability and non-dequantization are not mutually exclusive. We begin by providing a number of new somewhat broader definitions of the relevant concepts, compared to what is found in other literature, which are operationally motivated, and consistent with prior art. With these precise definitions given and motivated, we then study the relation between trainability and dequantization of variational QML. Next, we also discuss the degrees of "variationalness" of QML models, where we distinguish between models like the hardware efficient ansatz and quantum kernel methods. Finally, we introduce recipes for building PQC-based QML models which are both trainable and nondequantizable, and corresponding to different degrees of variationalness. We do not address the practical utility for such models. Our work however does point toward a way forward for finding more general constructions, for which finding applications may become feasible.

On the expressivity of embedding quantum kernels

One of the most natural connections between quantum and classical machine learning has been established in the context of kernel methods. Kernel methods rely on kernels, which are inner products of feature vectors living in large feature spaces. Quantum kernels are typically evaluated by explicitly constructing quantum feature states and then taking their inner product, here called embedding quantum kernels. Since classical kernels are usually evaluated without using the feature vectors explicitly, we wonder how expressive embedding quantum kernels are. In this work, we raise the fundamental question: can all quantum kernels be expressed as the inner product of quantum feature states? Our first result is positive: Invoking computational universality, we find that for any kernel function there always exists a corresponding quantum feature map and an embedding quantum kernel. The more operational reading of the question is concerned with efficient constructions, however. In a second part, we formalize the question of universality of efficient embedding quantum kernels. For shift-invariant kernels, we use the technique of random Fourier features to show that they are universal within the broad class of all kernels which allow a variant of efficient Fourier sampling. We then extend this result to a new class of so-called composition kernels, which we show also contains projected quantum kernels introduced in recent works. After proving the universality of embedding quantum kernels for both shift-invariant and composition kernels, we identify the directions towards new, more exotic, and unexplored quantum kernel families, for which it still remains open whether they correspond to efficient embedding quantum kernels.

Potential and limitations of random Fourier features for dequantizing quantum machine learning

Quantum machine learning is arguably one of the most explored applications of near-term quantum devices. Much focus has been put on notions of variational quantum machine learning where parameterized quantum circuits (PQCs) are used as learning models. These PQC models have a rich structure which suggests that they might be amenable to efficient dequantization via random Fourier features (RFF). In this work, we establish necessary and sufficient conditions under which RFF does indeed provide an efficient dequantization of variational quantum machine learning for regression. We build on these insights to make concrete suggestions for PQC architecture design, and to identify structures which are necessary for a regression problem to admit a potential quantum advantage via PQC based optimization.

Understanding quantum machine learning also requires rethinking generalization

Quantum machine learning models have shown successful generalization performance even when trained with few data. In this work, through systematic randomization experiments, we show that traditional approaches to understanding generalization fail to explain the behavior of such quantum models. Our experiments reveal that state-of-the-art quantum neural networks accurately fit random states and random labeling of training data. This ability to memorize random data defies current notions of small generalization error, problematizing approaches that build on complexity measures such as the VC dimension, the Rademacher complexity, and all their uniform relatives. We complement our empirical results with a theoretical construction showing that quantum neural networks can fit arbitrary labels to quantum states, hinting at their memorization ability. Our results do not preclude the possibility of good generalization with few training data but rather rule out any possible guarantees based only on the properties of the model family. These findings expose a fundamental challenge in the conventional understanding of generalization in quantum machine learning and highlight the need for a paradigm shift in the design of quantum models for machine learning tasks.

Exploiting symmetry in variational quantum machine learning

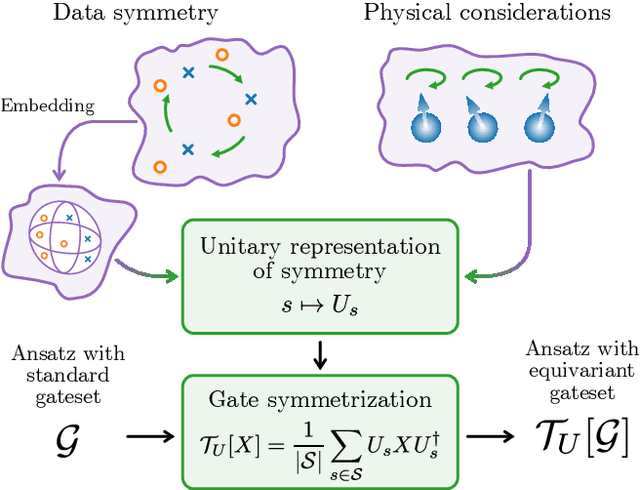
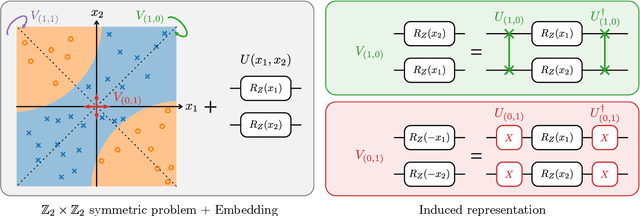
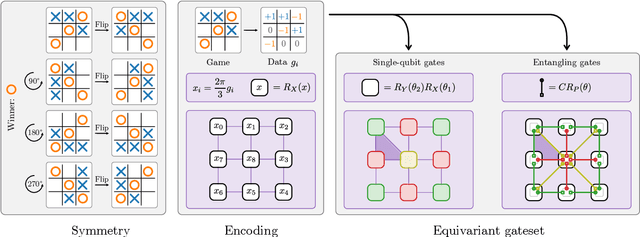
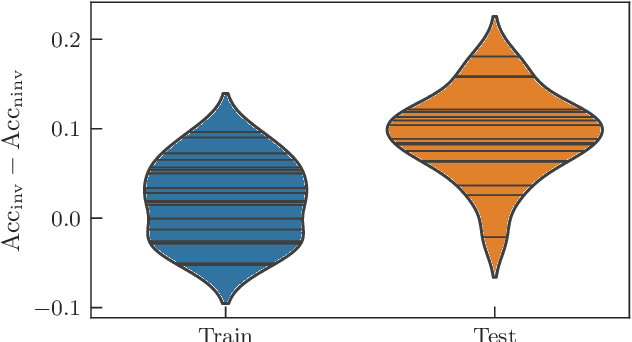
Variational quantum machine learning is an extensively studied application of near-term quantum computers. The success of variational quantum learning models crucially depends on finding a suitable parametrization of the model that encodes an inductive bias relevant to the learning task. However, precious little is known about guiding principles for the construction of suitable parametrizations. In this work, we holistically explore when and how symmetries of the learning problem can be exploited to construct quantum learning models with outcomes invariant under the symmetry of the learning task. Building on tools from representation theory, we show how a standard gateset can be transformed into an equivariant gateset that respects the symmetries of the problem at hand through a process of gate symmetrization. We benchmark the proposed methods on two toy problems that feature a non-trivial symmetry and observe a substantial increase in generalization performance. As our tools can also be applied in a straightforward way to other variational problems with symmetric structure, we show how equivariant gatesets can be used in variational quantum eigensolvers.

Encoding-dependent generalization bounds for parametrized quantum circuits

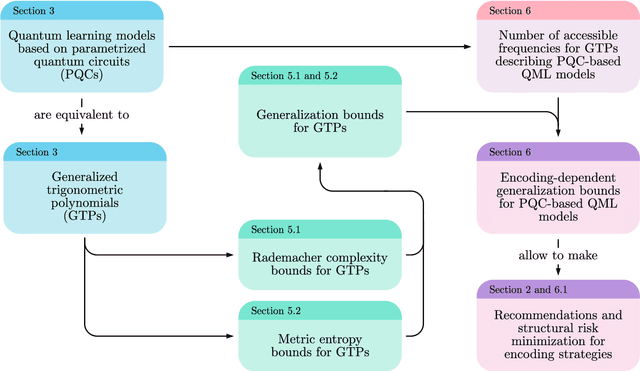
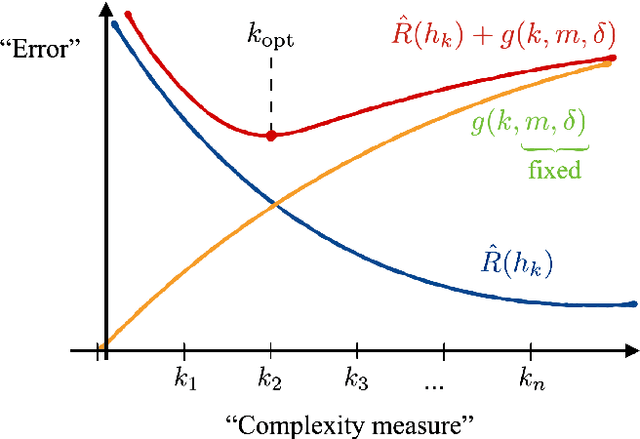
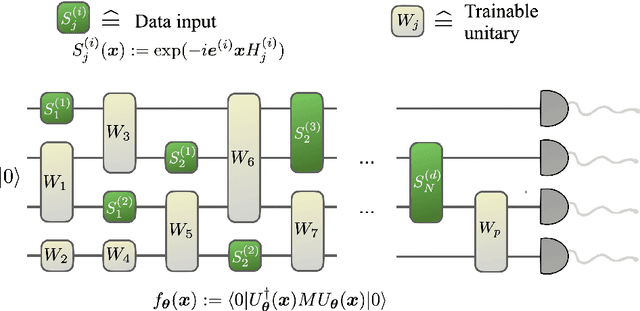
A large body of recent work has begun to explore the potential of parametrized quantum circuits (PQCs) as machine learning models, within the framework of hybrid quantum-classical optimization. In particular, theoretical guarantees on the out-of-sample performance of such models, in terms of generalization bounds, have emerged. However, none of these generalization bounds depend explicitly on how the classical input data is encoded into the PQC. We derive generalization bounds for PQC-based models that depend explicitly on the strategy used for data-encoding. These imply bounds on the performance of trained PQC-based models on unseen data. Moreover, our results facilitate the selection of optimal data-encoding strategies via structural risk minimization, a mathematically rigorous framework for model selection. We obtain our generalization bounds by bounding the complexity of PQC-based models as measured by the Rademacher complexity and the metric entropy, two complexity measures from statistical learning theory. To achieve this, we rely on a representation of PQC-based models via trigonometric functions. Our generalization bounds emphasize the importance of well-considered data-encoding strategies for PQC-based models.

Training Quantum Embedding Kernels on Near-Term Quantum Computers

Kernel methods are a cornerstone of classical machine learning. The idea of using quantum computers to compute kernels has recently attracted attention. Quantum embedding kernels (QEKs) constructed by embedding data into the Hilbert space of a quantum computer are a particular quantum kernel technique that allows to gather insights into learning problems and that are particularly suitable for noisy intermediate-scale quantum devices. In this work, we first provide an accessible introduction to quantum embedding kernels and then analyze the practical issues arising when realizing them on a noisy near-term quantum computer. We focus on quantum embedding kernels with variational parameters. These variational parameters are optimized for a given dataset by increasing the kernel-target alignment, a heuristic connected to the achievable classification accuracy. We further show under which conditions noise from device imperfections influences the predicted kernel and provide a strategy to mitigate these detrimental effects which is tailored to quantum embedding kernels. We also address the influence of finite sampling and derive bounds that put guarantees on the quality of the kernel matrix. We illustrate our findings by numerical experiments and tests on actual hardware.