Concept learning of parameterized quantum models from limited measurements

Classical learning of the expectation values of observables for quantum states is a natural variant of learning quantum states or channels. While learning-theoretic frameworks establish the sample complexity and the number of measurement shots per sample required for learning such statistical quantities, the interplay between these two variables has not been adequately quantified before. In this work, we take the probabilistic nature of quantum measurements into account in classical modelling and discuss these quantities under a single unified learning framework. We provide provable guarantees for learning parameterized quantum models that also quantify the asymmetrical effects and interplay of the two variables on the performance of learning algorithms. These results show that while increasing the sample size enhances the learning performance of classical machines, even with single-shot estimates, the improvements from increasing measurements become asymptotically trivial beyond a constant factor. We further apply our framework and theoretical guarantees to study the impact of measurement noise on the classical surrogation of parameterized quantum circuit models. Our work provides new tools to analyse the operational influence of finite measurement noise in the classical learning of quantum systems.

A Unified Framework for Trace-induced Quantum Kernels

Quantum kernel methods are promising candidates for achieving a practical quantum advantage for certain machine learning tasks. Similar to classical machine learning, an exact form of a quantum kernel is expected to have a great impact on the model performance. In this work we combine all trace-induced quantum kernels, including the commonly-used global fidelity and local projected quantum kernels, into a common framework. We show how generalized trace-induced quantum kernels can be constructed as combinations of the fundamental building blocks we coin "Lego" kernels, which impose an inductive bias on the resulting quantum models. We relate the expressive power and generalization ability to the number of non-zero weight Lego kernels and propose a systematic approach to increase the complexity of a quantum kernel model, leading to a new form of the local projected kernels that require fewer quantum resources in terms of the number of quantum gates and measurement shots. We show numerically that models based on local projected kernels can achieve comparable performance to the global fidelity quantum kernel. Our work unifies existing quantum kernels and provides a systematic framework to compare their properties.

Fock State-enhanced Expressivity of Quantum Machine Learning Models

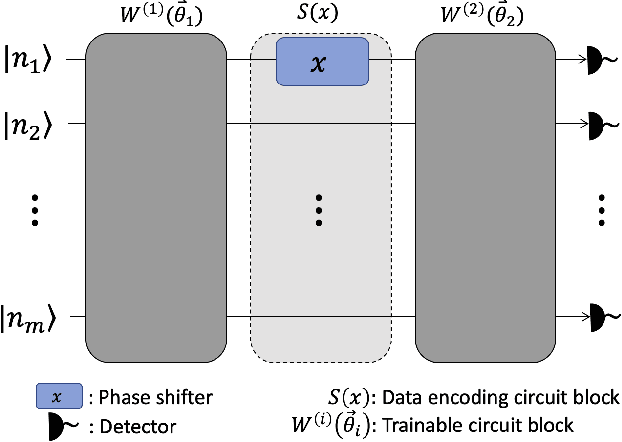
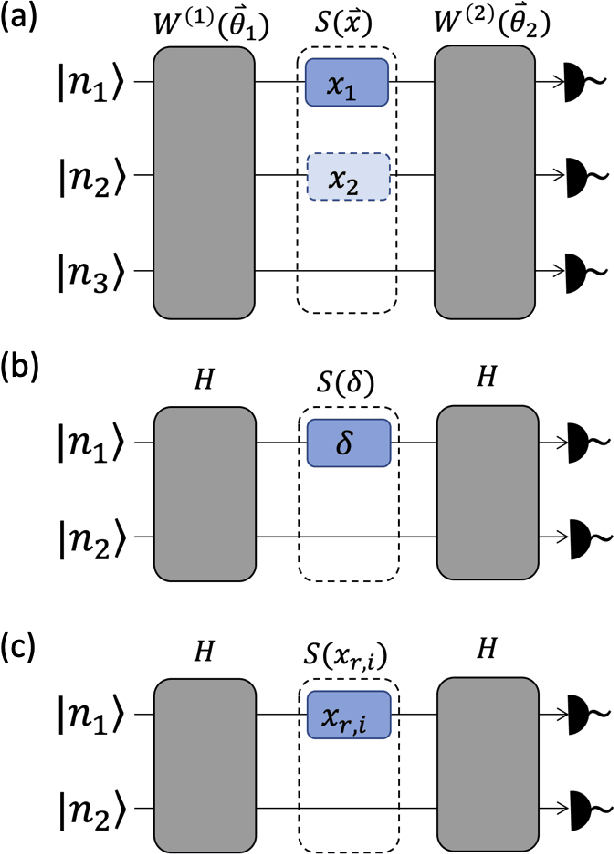
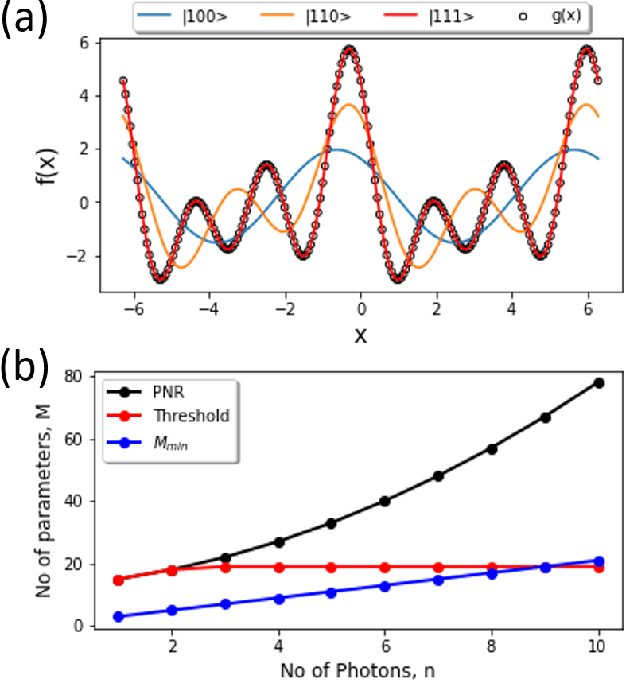
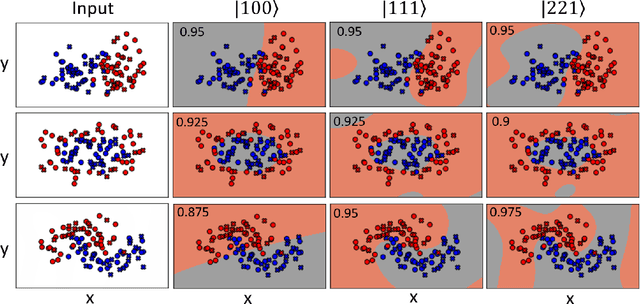
The data-embedding process is one of the bottlenecks of quantum machine learning, potentially negating any quantum speedups. In light of this, more effective data-encoding strategies are necessary. We propose a photonic-based bosonic data-encoding scheme that embeds classical data points using fewer encoding layers and circumventing the need for nonlinear optical components by mapping the data points into the high-dimensional Fock space. The expressive power of the circuit can be controlled via the number of input photons. Our work shed some light on the unique advantages offers by quantum photonics on the expressive power of quantum machine learning models. By leveraging the photon-number dependent expressive power, we propose three different noisy intermediate-scale quantum-compatible binary classification methods with different scaling of required resources suitable for different supervised classification tasks.