Data-driven model reconstruction for nonlinear wave dynamics

The use of machine learning to predict wave dynamics is a topic of growing interest, but commonly-used deep learning approaches suffer from a lack of interpretability of the trained models. Here we present an interpretable machine learning framework for analyzing the nonlinear evolution dynamics of optical wavepackets in complex wave media. We use sparse regression to reduce microscopic discrete lattice models to simpler effective continuum models which can accurately describe the dynamics of the wavepacket envelope. We apply our approach to valley-Hall domain walls in honeycomb photonic lattices of laser-written waveguides with Kerr-type nonlinearity and different boundary shapes. The reconstructed equations accurately reproduce the linear dispersion and nonlinear effects including self-steepening and self-focusing. This scheme is proven free of the a priori limitations imposed by the underlying hierarchy of scales traditionally employed in asymptotic analytical methods. It represents a powerful interpretable machine learning technique of interest for advancing design capabilities in photonics and framing the complex interaction-driven dynamics in various topological materials.

Res-U2Net: Untrained Deep Learning for Phase Retrieval and Image Reconstruction

Conventional deep learning-based image reconstruction methods require a large amount of training data which can be hard to obtain in practice. Untrained deep learning methods overcome this limitation by training a network to invert a physical model of the image formation process. Here we present a novel untrained Res-U2Net model for phase retrieval. We use the extracted phase information to determine changes in an object's surface and generate a mesh representation of its 3D structure. We compare the performance of Res-U2Net phase retrieval against UNet and U2Net using images from the GDXRAY dataset.

A Unified Framework for Trace-induced Quantum Kernels

Quantum kernel methods are promising candidates for achieving a practical quantum advantage for certain machine learning tasks. Similar to classical machine learning, an exact form of a quantum kernel is expected to have a great impact on the model performance. In this work we combine all trace-induced quantum kernels, including the commonly-used global fidelity and local projected quantum kernels, into a common framework. We show how generalized trace-induced quantum kernels can be constructed as combinations of the fundamental building blocks we coin "Lego" kernels, which impose an inductive bias on the resulting quantum models. We relate the expressive power and generalization ability to the number of non-zero weight Lego kernels and propose a systematic approach to increase the complexity of a quantum kernel model, leading to a new form of the local projected kernels that require fewer quantum resources in terms of the number of quantum gates and measurement shots. We show numerically that models based on local projected kernels can achieve comparable performance to the global fidelity quantum kernel. Our work unifies existing quantum kernels and provides a systematic framework to compare their properties.

Identifying topology of leaky photonic lattices with machine learning

We show how machine learning techniques can be applied for the classification of topological phases in leaky photonic lattices using limited measurement data. We propose an approach based solely on bulk intensity measurements, thus exempt from the need for complicated phase retrieval procedures. In particular, we design a fully connected neural network that accurately determines topological properties from the output intensity distribution in dimerized waveguide arrays with leaky channels, after propagation of a spatially localized initial excitation at a finite distance, in a setting that closely emulates realistic experimental conditions.

Dark soliton detection using persistent homology

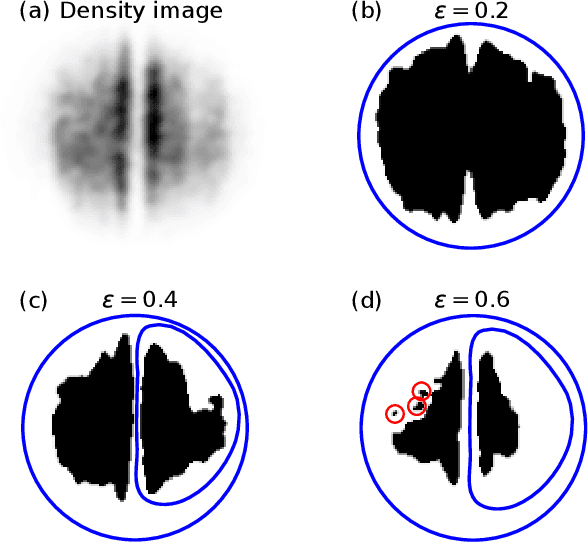
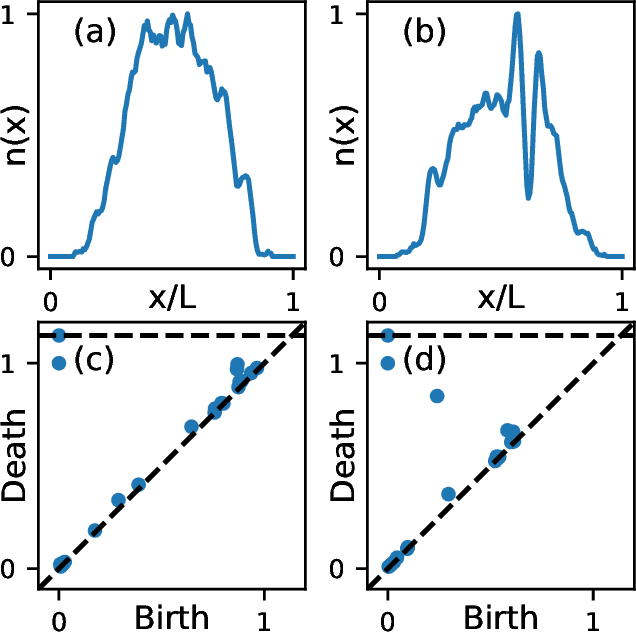
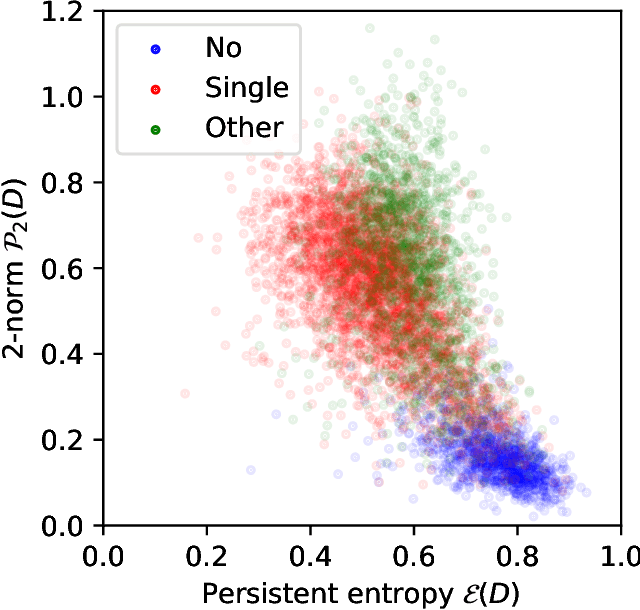
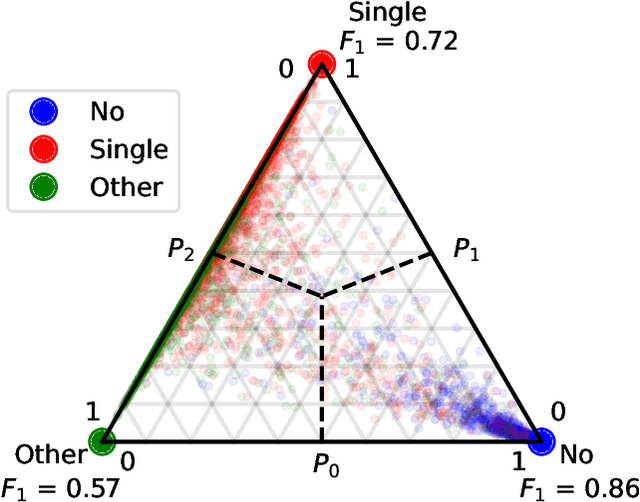
Classifying experimental image data often requires manual identification of qualitative features, which is difficult to automate. Existing automated approaches based on deep convolutional neural networks can achieve accuracy comparable to human classifiers, but require extensive training data and computational resources. Here we show that the emerging framework of topological data analysis can be used to rapidly and reliably identify qualitative features in image data, enabling their classification using easily-interpretable linear models. Specifically, we consider the task of identifying dark solitons using a freely-available dataset of 6257 labelled Bose-Einstein condensate (BEC) density images. We use point summaries of the images' topological features -- their persistent entropy and lifetime $p$-norms -- to train logistic regression models. The models attain performance comparable to neural networks using a fraction of the training data, classifying images 30 times faster.

Fock State-enhanced Expressivity of Quantum Machine Learning Models

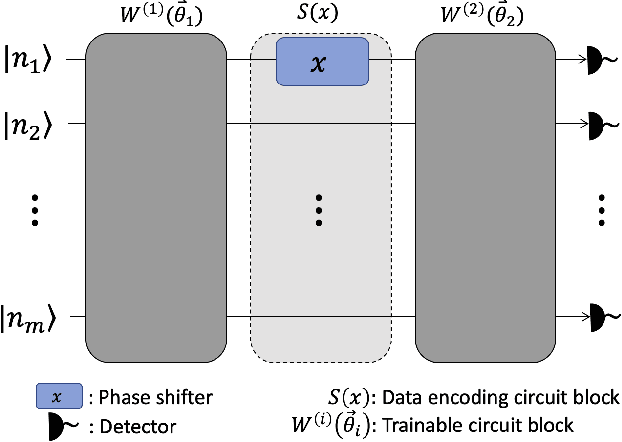
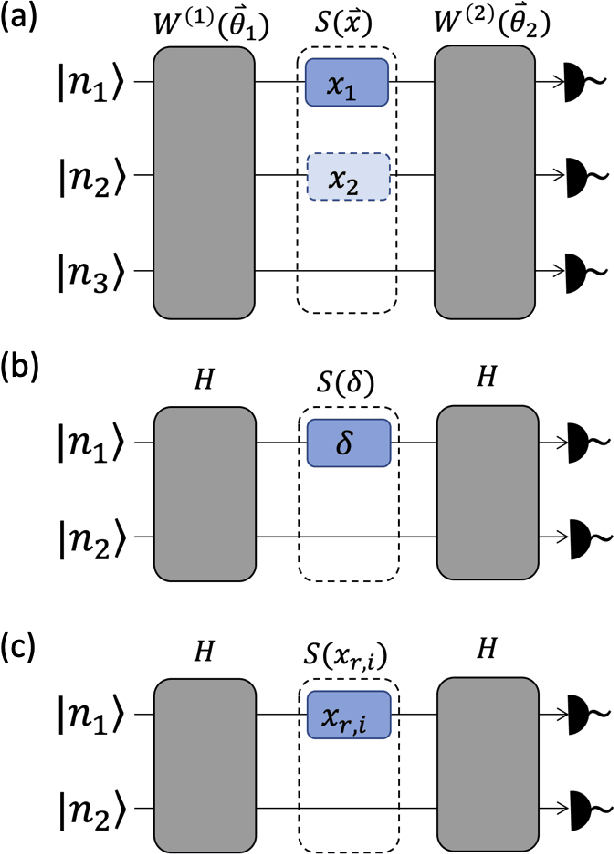
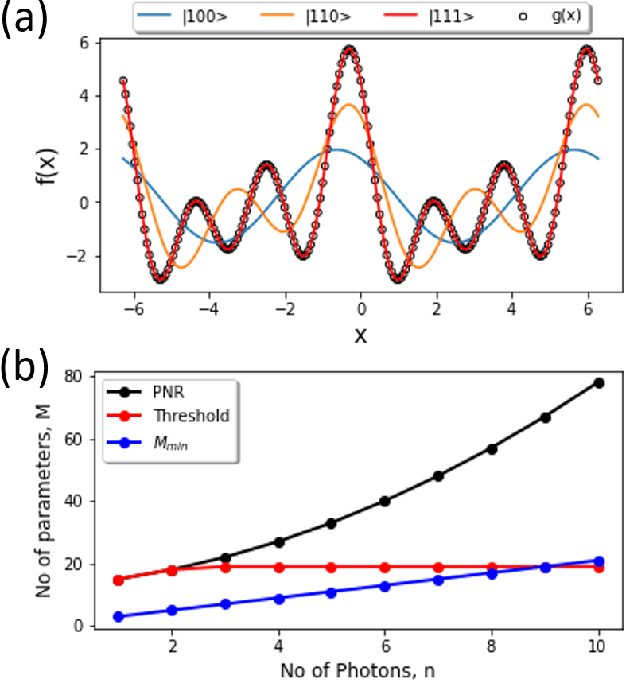
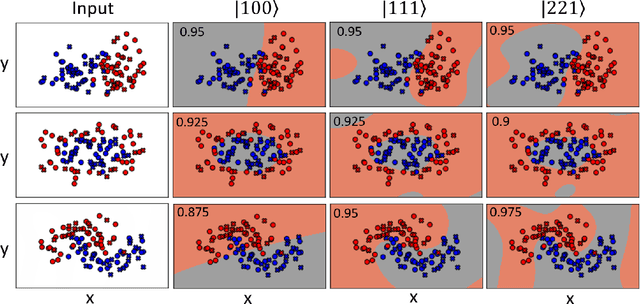
The data-embedding process is one of the bottlenecks of quantum machine learning, potentially negating any quantum speedups. In light of this, more effective data-encoding strategies are necessary. We propose a photonic-based bosonic data-encoding scheme that embeds classical data points using fewer encoding layers and circumventing the need for nonlinear optical components by mapping the data points into the high-dimensional Fock space. The expressive power of the circuit can be controlled via the number of input photons. Our work shed some light on the unique advantages offers by quantum photonics on the expressive power of quantum machine learning models. By leveraging the photon-number dependent expressive power, we propose three different noisy intermediate-scale quantum-compatible binary classification methods with different scaling of required resources suitable for different supervised classification tasks.