Cautious optimism for deep parameterized quantum circuits

A central challenge in quantum machine learning is understanding the scaling behavior of parameterized quantum circuits (PQCs). In particular, it remains unclear how their performance on unseen data changes as the number of trainable parameters increases. Prior works have derived formal generalization guarantees for quantum models, but it is well-known that many such results do not fully characterize generalization behavior in practice. In this work, we show that gradient-based PQCs can exhibit improved performance on unseen data as model size increases, displaying the phenomenon of double descent. This contrasts with the traditional view that larger models lead to degraded generalization. We provide analytical results rigorously underpinning this behavior by leveraging add-one-in perturbation techniques and spectral properties of random matrices. We support these results with numerical experiments on re-uploading PQCs across several data sets and training set sizes, consistently observing the predicted double descent behavior. While other obstacles on the path toward practical quantum machine learning remain, our finding that deeper parameterized quantum circuits do not necessarily exhibit degraded performance provides reasons for cautious optimism.

Distribution and volume based scoring for Isolation Forests

We make two contributions to the Isolation Forest method for anomaly and outlier detection. The first contribution is an information-theoretically motivated generalisation of the score function that is used to aggregate the scores across random tree estimators. This generalisation allows one to take into account not just the ensemble average across trees but instead the whole distribution. The second contribution is an alternative scoring function at the level of the individual tree estimator, in which we replace the depth-based scoring of the Isolation Forest with one based on hyper-volumes associated to an isolation tree's leaf nodes. We motivate the use of both of these methods on generated data and also evaluate them on 34 datasets from the recent and exhaustive ``ADBench'' benchmark, finding significant improvement over the standard isolation forest for both variants on some datasets and improvement on average across all datasets for one of the two variants. The code to reproduce our results is made available as part of the submission.

Exploiting symmetry in variational quantum machine learning

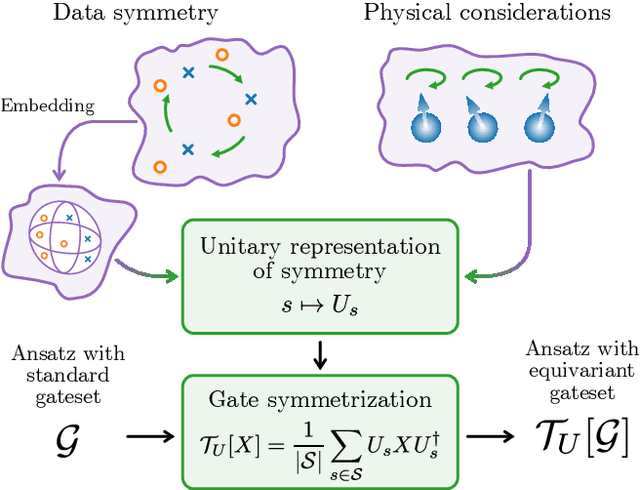
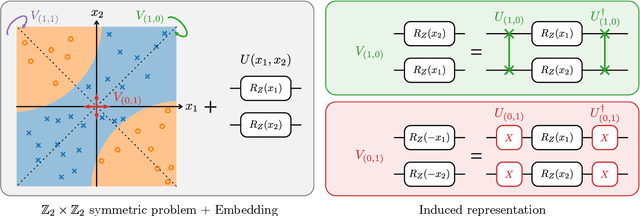
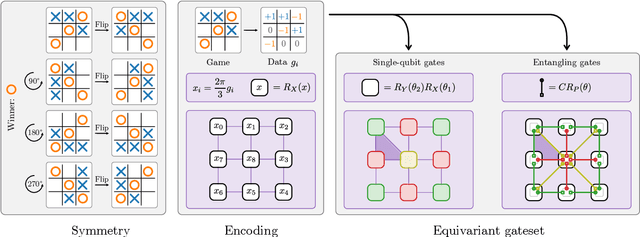
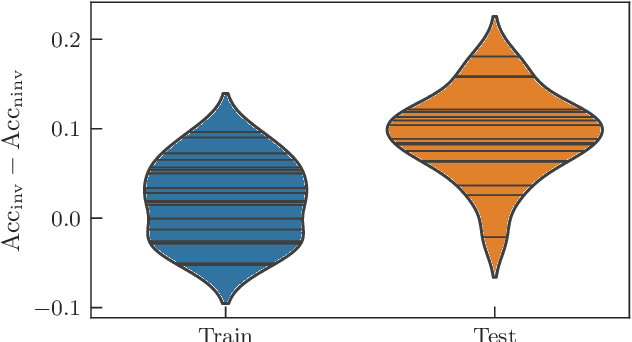
Variational quantum machine learning is an extensively studied application of near-term quantum computers. The success of variational quantum learning models crucially depends on finding a suitable parametrization of the model that encodes an inductive bias relevant to the learning task. However, precious little is known about guiding principles for the construction of suitable parametrizations. In this work, we holistically explore when and how symmetries of the learning problem can be exploited to construct quantum learning models with outcomes invariant under the symmetry of the learning task. Building on tools from representation theory, we show how a standard gateset can be transformed into an equivariant gateset that respects the symmetries of the problem at hand through a process of gate symmetrization. We benchmark the proposed methods on two toy problems that feature a non-trivial symmetry and observe a substantial increase in generalization performance. As our tools can also be applied in a straightforward way to other variational problems with symmetric structure, we show how equivariant gatesets can be used in variational quantum eigensolvers.