Paul Boes
FARSEC: A Reproducible Framework for Automatic Real-Time Vehicle Speed Estimation Using Traffic Cameras
Sep 25, 2023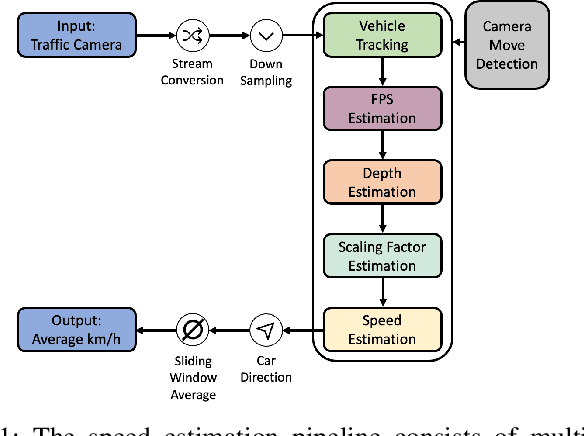
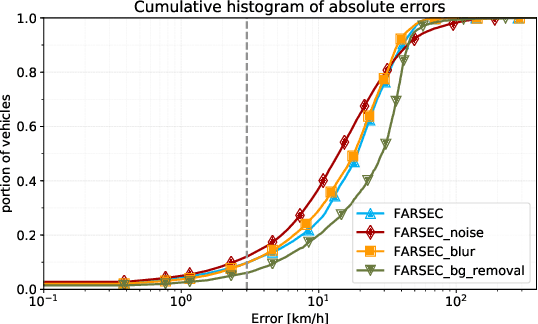


Abstract:Estimating the speed of vehicles using traffic cameras is a crucial task for traffic surveillance and management, enabling more optimal traffic flow, improved road safety, and lower environmental impact. Transportation-dependent systems, such as for navigation and logistics, have great potential to benefit from reliable speed estimation. While there is prior research in this area reporting competitive accuracy levels, their solutions lack reproducibility and robustness across different datasets. To address this, we provide a novel framework for automatic real-time vehicle speed calculation, which copes with more diverse data from publicly available traffic cameras to achieve greater robustness. Our model employs novel techniques to estimate the length of road segments via depth map prediction. Additionally, our framework is capable of handling realistic conditions such as camera movements and different video stream inputs automatically. We compare our model to three well-known models in the field using their benchmark datasets. While our model does not set a new state of the art regarding prediction performance, the results are competitive on realistic CCTV videos. At the same time, our end-to-end pipeline offers more consistent results, an easier implementation, and better compatibility. Its modular structure facilitates reproducibility and future improvements.
Using deep learning to construct stochastic local search SAT solvers with performance bounds
Sep 23, 2023



Abstract:The Boolean Satisfiability problem (SAT) is the most prototypical NP-complete problem and of great practical relevance. One important class of solvers for this problem are stochastic local search (SLS) algorithms that iteratively and randomly update a candidate assignment. Recent breakthrough results in theoretical computer science have established sufficient conditions under which SLS solvers are guaranteed to efficiently solve a SAT instance, provided they have access to suitable "oracles" that provide samples from an instance-specific distribution, exploiting an instance's local structure. Motivated by these results and the well established ability of neural networks to learn common structure in large datasets, in this work, we train oracles using Graph Neural Networks and evaluate them on two SLS solvers on random SAT instances of varying difficulty. We find that access to GNN-based oracles significantly boosts the performance of both solvers, allowing them, on average, to solve 17% more difficult instances (as measured by the ratio between clauses and variables), and to do so in 35% fewer steps, with improvements in the median number of steps of up to a factor of 8. As such, this work bridges formal results from theoretical computer science and practically motivated research on deep learning for constraint satisfaction problems and establishes the promise of purpose-trained SAT solvers with performance guarantees.
Distribution and volume based scoring for Isolation Forests
Sep 20, 2023Abstract:We make two contributions to the Isolation Forest method for anomaly and outlier detection. The first contribution is an information-theoretically motivated generalisation of the score function that is used to aggregate the scores across random tree estimators. This generalisation allows one to take into account not just the ensemble average across trees but instead the whole distribution. The second contribution is an alternative scoring function at the level of the individual tree estimator, in which we replace the depth-based scoring of the Isolation Forest with one based on hyper-volumes associated to an isolation tree's leaf nodes. We motivate the use of both of these methods on generated data and also evaluate them on 34 datasets from the recent and exhaustive ``ADBench'' benchmark, finding significant improvement over the standard isolation forest for both variants on some datasets and improvement on average across all datasets for one of the two variants. The code to reproduce our results is made available as part of the submission.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge