Certifiably Robust Encoding Schemes

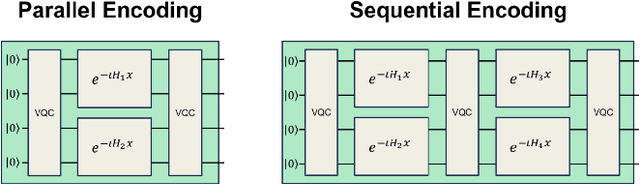
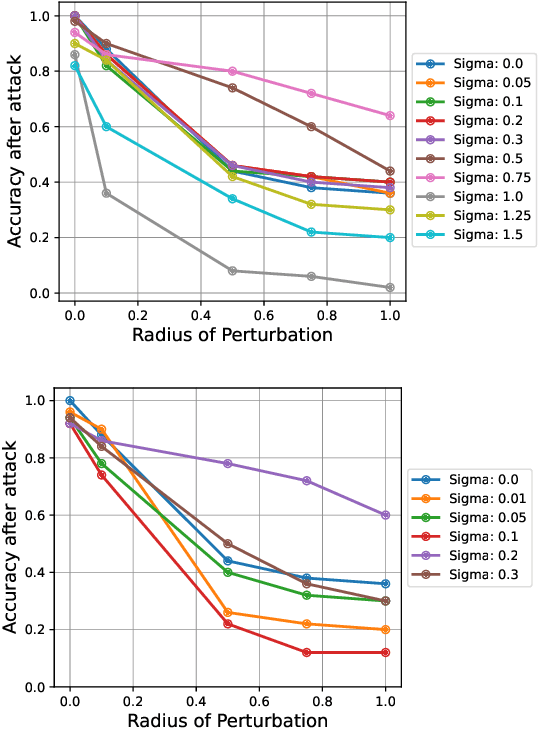
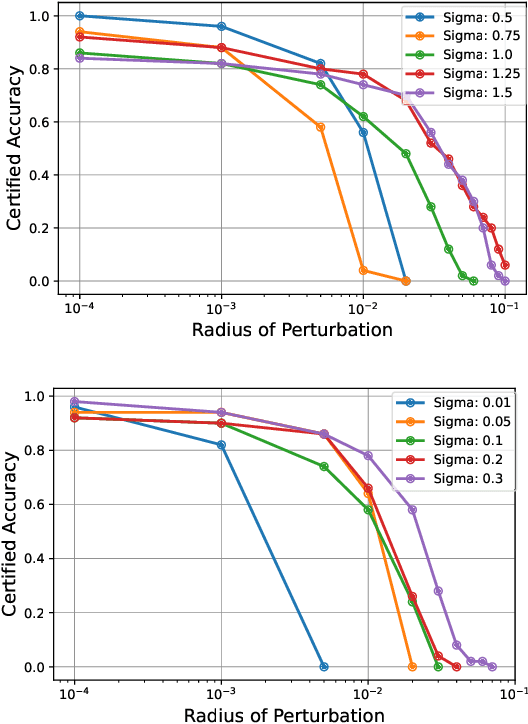
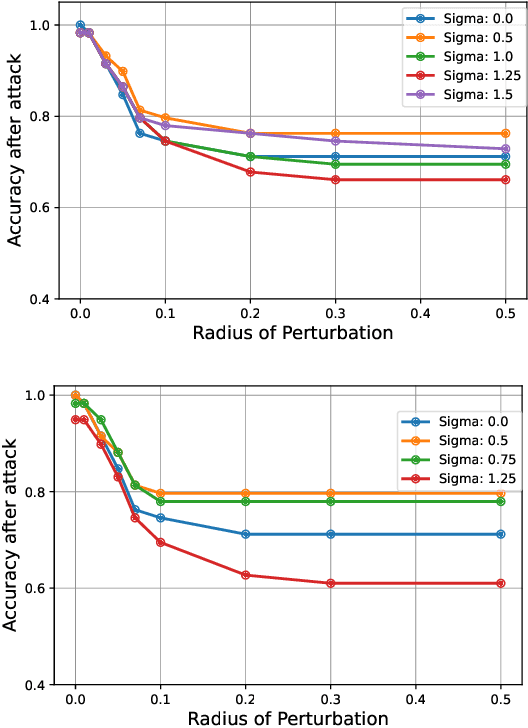
Quantum machine learning uses principles from quantum mechanics to process data, offering potential advances in speed and performance. However, previous work has shown that these models are susceptible to attacks that manipulate input data or exploit noise in quantum circuits. Following this, various studies have explored the robustness of these models. These works focus on the robustness certification of manipulations of the quantum states. We extend this line of research by investigating the robustness against perturbations in the classical data for a general class of data encoding schemes. We show that for such schemes, the addition of suitable noise channels is equivalent to evaluating the mean value of the noiseless classifier at the smoothed data, akin to Randomized Smoothing from classical machine learning. Using our general framework, we show that suitable additions of phase-damping noise channels improve empirical and provable robustness for the considered class of encoding schemes.

Discrete Randomized Smoothing Meets Quantum Computing

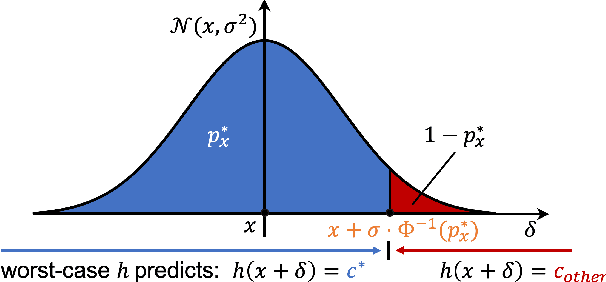
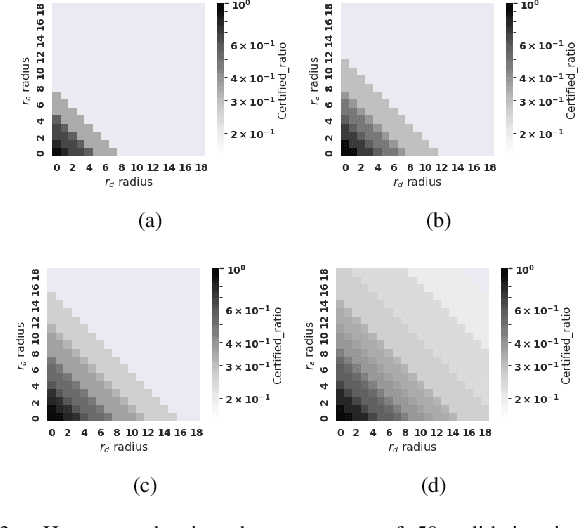
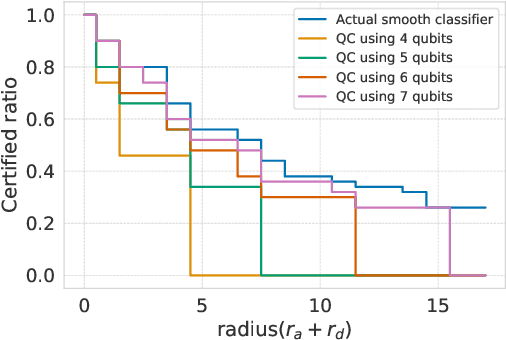
Breakthroughs in machine learning (ML) and advances in quantum computing (QC) drive the interdisciplinary field of quantum machine learning to new levels. However, due to the susceptibility of ML models to adversarial attacks, practical use raises safety-critical concerns. Existing Randomized Smoothing (RS) certification methods for classical machine learning models are computationally intensive. In this paper, we propose the combination of QC and the concept of discrete randomized smoothing to speed up the stochastic certification of ML models for discrete data. We show how to encode all the perturbations of the input binary data in superposition and use Quantum Amplitude Estimation (QAE) to obtain a quadratic reduction in the number of calls to the model that are required compared to traditional randomized smoothing techniques. In addition, we propose a new binary threat model to allow for an extensive evaluation of our approach on images, graphs, and text.

Quadratic Advantage with Quantum Randomized Smoothing Applied to Time-Series Analysis

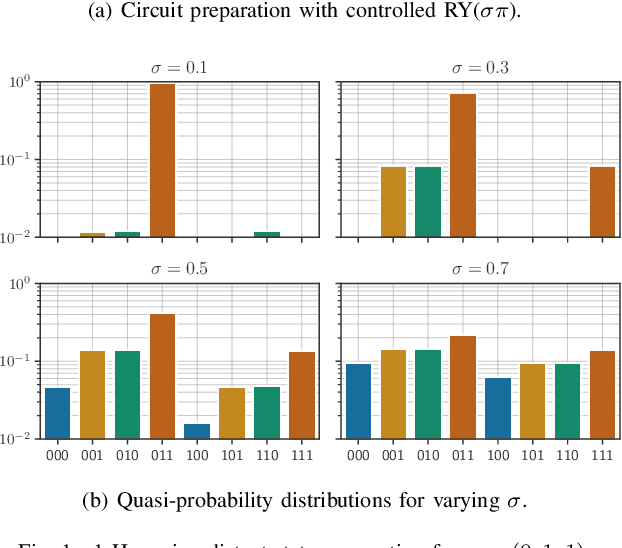
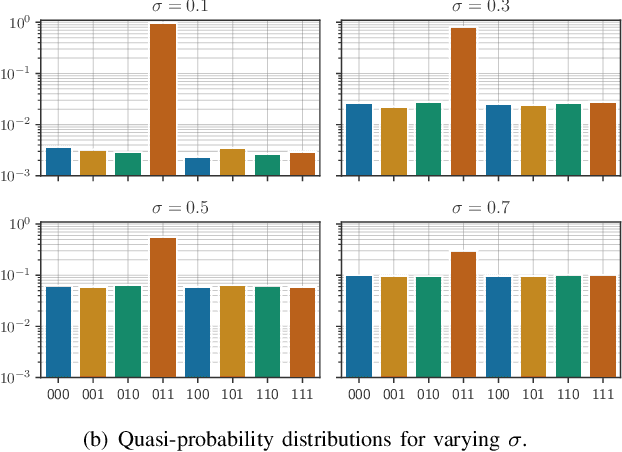
As quantum machine learning continues to develop at a rapid pace, the importance of ensuring the robustness and efficiency of quantum algorithms cannot be overstated. Our research presents an analysis of quantum randomized smoothing, how data encoding and perturbation modeling approaches can be matched to achieve meaningful robustness certificates. By utilizing an innovative approach integrating Grover's algorithm, a quadratic sampling advantage over classical randomized smoothing is achieved. This strategy necessitates a basis state encoding, thus restricting the space of meaningful perturbations. We show how constrained $k$-distant Hamming weight perturbations are a suitable noise distribution here, and elucidate how they can be constructed on a quantum computer. The efficacy of the proposed framework is demonstrated on a time series classification task employing a Bag-of-Words pre-processing solution. The advantage of quadratic sample reduction is recovered especially in the regime with large number of samples. This may allow quantum computers to efficiently scale randomized smoothing to more complex tasks beyond the reach of classical methods.

Constructing Optimal Noise Channels for Enhanced Robustness in Quantum Machine Learning

With the rapid advancement of Quantum Machine Learning (QML), the critical need to enhance security measures against adversarial attacks and protect QML models becomes increasingly evident. In this work, we outline the connection between quantum noise channels and differential privacy (DP), by constructing a family of noise channels which are inherently $\epsilon$-DP: $(\alpha, \gamma)$-channels. Through this approach, we successfully replicate the $\epsilon$-DP bounds observed for depolarizing and random rotation channels, thereby affirming the broad generality of our framework. Additionally, we use a semi-definite program to construct an optimally robust channel. In a small-scale experimental evaluation, we demonstrate the benefits of using our optimal noise channel over depolarizing noise, particularly in enhancing adversarial accuracy. Moreover, we assess how the variables $\alpha$ and $\gamma$ affect the certifiable robustness and investigate how different encoding methods impact the classifier's robustness.

Quantum Neural Networks under Depolarization Noise: Exploring White-Box Attacks and Defenses

Leveraging the unique properties of quantum mechanics, Quantum Machine Learning (QML) promises computational breakthroughs and enriched perspectives where traditional systems reach their boundaries. However, similarly to classical machine learning, QML is not immune to adversarial attacks. Quantum adversarial machine learning has become instrumental in highlighting the weak points of QML models when faced with adversarial crafted feature vectors. Diving deep into this domain, our exploration shines light on the interplay between depolarization noise and adversarial robustness. While previous results enhanced robustness from adversarial threats through depolarization noise, our findings paint a different picture. Interestingly, adding depolarization noise discontinued the effect of providing further robustness for a multi-class classification scenario. Consolidating our findings, we conducted experiments with a multi-class classifier adversarially trained on gate-based quantum simulators, further elucidating this unexpected behavior.

Efficient MILP Decomposition in Quantum Computing for ReLU Network Robustness

Emerging quantum computing technologies, such as Noisy Intermediate-Scale Quantum (NISQ) devices, offer potential advancements in solving mathematical optimization problems. However, limitations in qubit availability, noise, and errors pose challenges for practical implementation. In this study, we examine two decomposition methods for Mixed-Integer Linear Programming (MILP) designed to reduce the original problem size and utilize available NISQ devices more efficiently. We concentrate on breaking down the original problem into smaller subproblems, which are then solved iteratively using a combined quantum-classical hardware approach. We conduct a detailed analysis for the decomposition of MILP with Benders and Dantzig-Wolfe methods. In our analysis, we show that the number of qubits required to solve Benders is exponentially large in the worst-case, while remains constant for Dantzig-Wolfe. Additionally, we leverage Dantzig-Wolfe decomposition on the use-case of certifying the robustness of ReLU networks. Our experimental results demonstrate that this approach can save up to 90\% of qubits compared to existing methods on quantum annealing and gate-based quantum computers.

Diffusion Denoised Smoothing for Certified and Adversarial Robust Out-Of-Distribution Detection

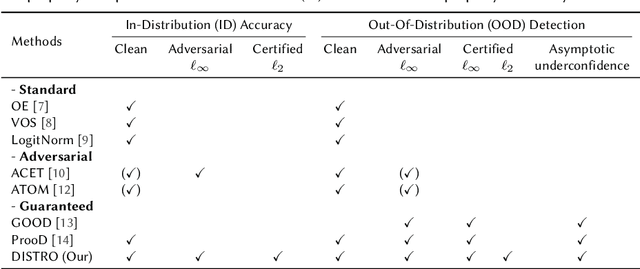
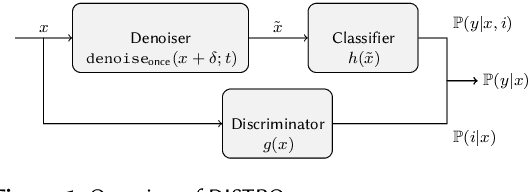
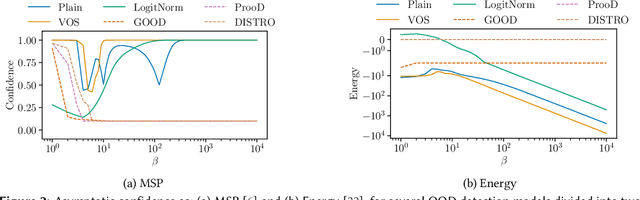
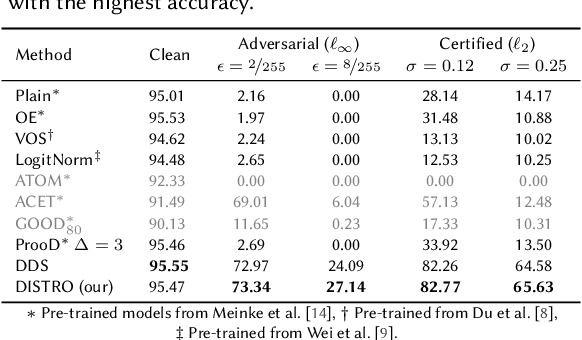
As the use of machine learning continues to expand, the importance of ensuring its safety cannot be overstated. A key concern in this regard is the ability to identify whether a given sample is from the training distribution, or is an "Out-Of-Distribution" (OOD) sample. In addition, adversaries can manipulate OOD samples in ways that lead a classifier to make a confident prediction. In this study, we present a novel approach for certifying the robustness of OOD detection within a $\ell_2$-norm around the input, regardless of network architecture and without the need for specific components or additional training. Further, we improve current techniques for detecting adversarial attacks on OOD samples, while providing high levels of certified and adversarial robustness on in-distribution samples. The average of all OOD detection metrics on CIFAR10/100 shows an increase of $\sim 13 \% / 5\%$ relative to previous approaches.