PICZL: Image-based Photometric Redshifts for AGN

Computing photo-z for AGN is challenging, primarily due to the interplay of relative emissions associated with the SMBH and its host galaxy. SED fitting methods, effective in pencil-beam surveys, face limitations in all-sky surveys with fewer bands available, lacking the ability to capture the AGN contribution to the SED accurately. This limitation affects the many 10s of millions of AGN clearly singled out and identified by SRG/eROSITA. Our goal is to significantly enhance photometric redshift performance for AGN in all-sky surveys while avoiding the need to merge multiple data sets. Instead, we employ readily available data products from the 10th Data Release of the Imaging Legacy Survey for DESI, covering > 20,000 deg$^{2}$ with deep images and catalog-based photometry in the grizW1-W4 bands. We introduce PICZL, a machine-learning algorithm leveraging an ensemble of CNNs. Utilizing a cross-channel approach, the algorithm integrates distinct SED features from images with those obtained from catalog-level data. Full probability distributions are achieved via the integration of Gaussian mixture models. On a validation sample of 8098 AGN, PICZL achieves a variance $\sigma_{\textrm{NMAD}}$ of 4.5% with an outlier fraction $\eta$ of 5.6%, outperforming previous attempts to compute accurate photo-z for AGN using ML. We highlight that the model's performance depends on many variables, predominantly the depth of the data. A thorough evaluation of these dependencies is presented in the paper. Our streamlined methodology maintains consistent performance across the entire survey area when accounting for differing data quality. The same approach can be adopted for future deep photometric surveys such as LSST and Euclid, showcasing its potential for wide-scale realisation. With this paper, we release updated photo-z (including errors) for the XMM-SERVS W-CDF-S, ELAIS-S1 and LSS fields.

Certifiably Robust Encoding Schemes

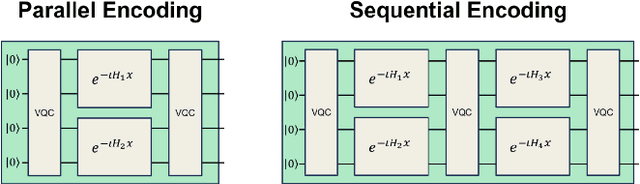
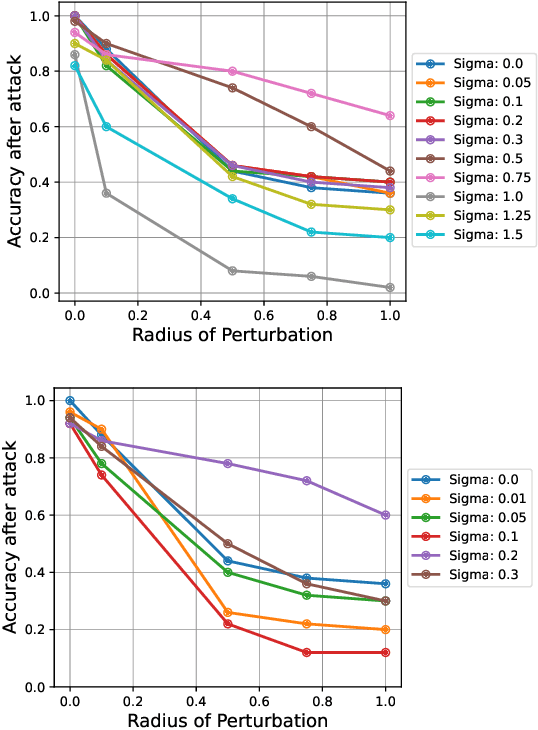
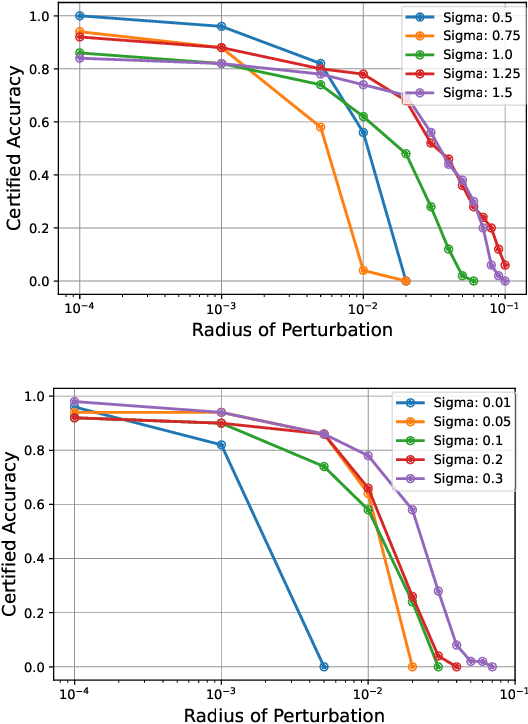
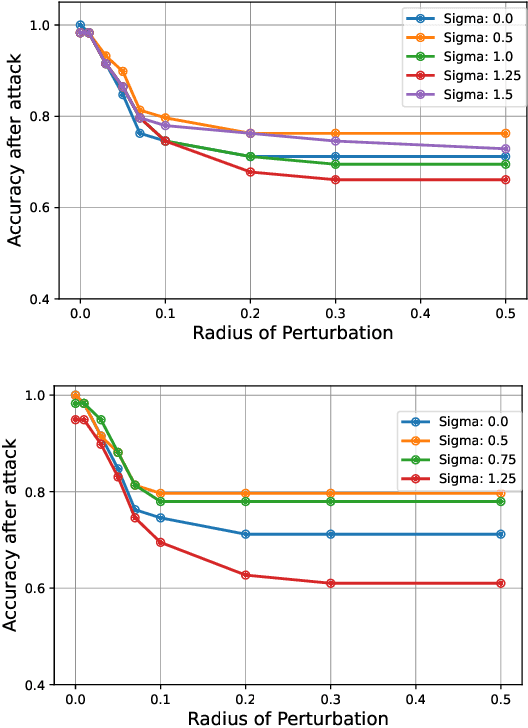
Quantum machine learning uses principles from quantum mechanics to process data, offering potential advances in speed and performance. However, previous work has shown that these models are susceptible to attacks that manipulate input data or exploit noise in quantum circuits. Following this, various studies have explored the robustness of these models. These works focus on the robustness certification of manipulations of the quantum states. We extend this line of research by investigating the robustness against perturbations in the classical data for a general class of data encoding schemes. We show that for such schemes, the addition of suitable noise channels is equivalent to evaluating the mean value of the noiseless classifier at the smoothed data, akin to Randomized Smoothing from classical machine learning. Using our general framework, we show that suitable additions of phase-damping noise channels improve empirical and provable robustness for the considered class of encoding schemes.

Discrete Randomized Smoothing Meets Quantum Computing

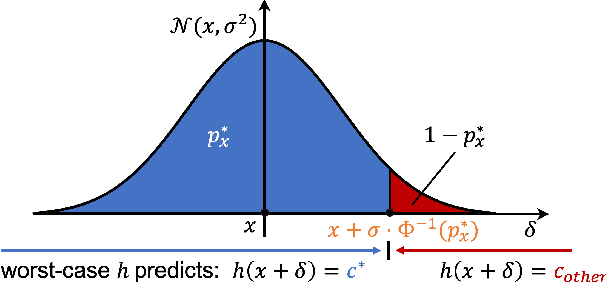
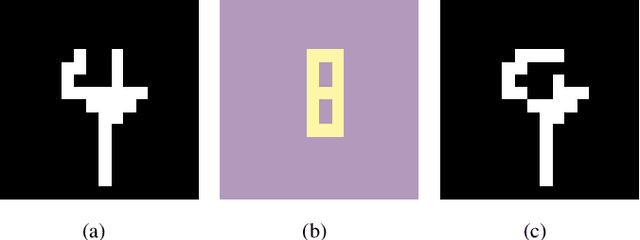
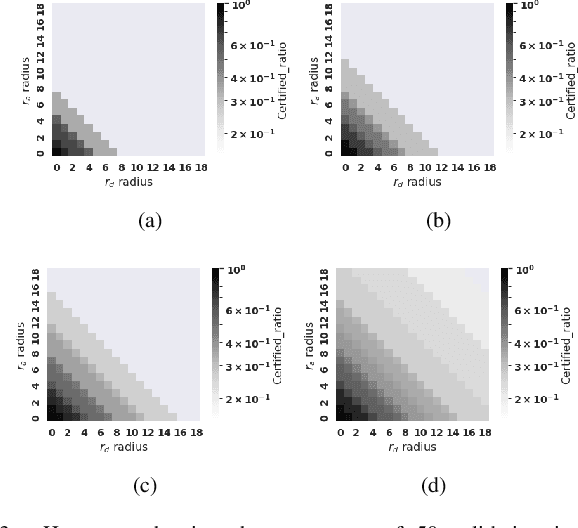
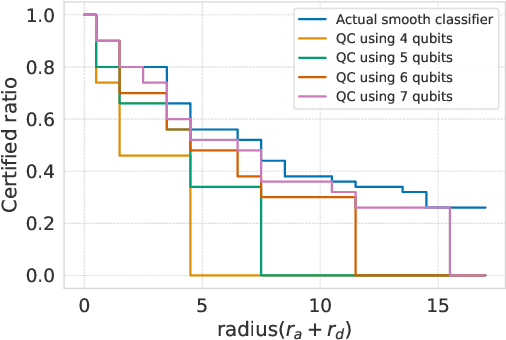
Breakthroughs in machine learning (ML) and advances in quantum computing (QC) drive the interdisciplinary field of quantum machine learning to new levels. However, due to the susceptibility of ML models to adversarial attacks, practical use raises safety-critical concerns. Existing Randomized Smoothing (RS) certification methods for classical machine learning models are computationally intensive. In this paper, we propose the combination of QC and the concept of discrete randomized smoothing to speed up the stochastic certification of ML models for discrete data. We show how to encode all the perturbations of the input binary data in superposition and use Quantum Amplitude Estimation (QAE) to obtain a quadratic reduction in the number of calls to the model that are required compared to traditional randomized smoothing techniques. In addition, we propose a new binary threat model to allow for an extensive evaluation of our approach on images, graphs, and text.