The Geometry of Refusal in Large Language Models: Concept Cones and Representational Independence

The safety alignment of large language models (LLMs) can be circumvented through adversarially crafted inputs, yet the mechanisms by which these attacks bypass safety barriers remain poorly understood. Prior work suggests that a single refusal direction in the model's activation space determines whether an LLM refuses a request. In this study, we propose a novel gradient-based approach to representation engineering and use it to identify refusal directions. Contrary to prior work, we uncover multiple independent directions and even multi-dimensional concept cones that mediate refusal. Moreover, we show that orthogonality alone does not imply independence under intervention, motivating the notion of representational independence that accounts for both linear and non-linear effects. Using this framework, we identify mechanistically independent refusal directions. We show that refusal mechanisms in LLMs are governed by complex spatial structures and identify functionally independent directions, confirming that multiple distinct mechanisms drive refusal behavior. Our gradient-based approach uncovers these mechanisms and can further serve as a foundation for future work on understanding LLMs.

REINFORCE Adversarial Attacks on Large Language Models: An Adaptive, Distributional, and Semantic Objective

To circumvent the alignment of large language models (LLMs), current optimization-based adversarial attacks usually craft adversarial prompts by maximizing the likelihood of a so-called affirmative response. An affirmative response is a manually designed start of a harmful answer to an inappropriate request. While it is often easy to craft prompts that yield a substantial likelihood for the affirmative response, the attacked model frequently does not complete the response in a harmful manner. Moreover, the affirmative objective is usually not adapted to model-specific preferences and essentially ignores the fact that LLMs output a distribution over responses. If low attack success under such an objective is taken as a measure of robustness, the true robustness might be grossly overestimated. To alleviate these flaws, we propose an adaptive and semantic optimization problem over the population of responses. We derive a generally applicable objective via the REINFORCE policy-gradient formalism and demonstrate its efficacy with the state-of-the-art jailbreak algorithms Greedy Coordinate Gradient (GCG) and Projected Gradient Descent (PGD). For example, our objective doubles the attack success rate (ASR) on Llama3 and increases the ASR from 2% to 50% with circuit breaker defense.

Adversarial Alignment for LLMs Requires Simpler, Reproducible, and More Measurable Objectives

Misaligned research objectives have considerably hindered progress in adversarial robustness research over the past decade. For instance, an extensive focus on optimizing target metrics, while neglecting rigorous standardized evaluation, has led researchers to pursue ad-hoc heuristic defenses that were seemingly effective. Yet, most of these were exposed as flawed by subsequent evaluations, ultimately contributing little measurable progress to the field. In this position paper, we illustrate that current research on the robustness of large language models (LLMs) risks repeating past patterns with potentially worsened real-world implications. To address this, we argue that realigned objectives are necessary for meaningful progress in adversarial alignment. To this end, we build on established cybersecurity taxonomy to formally define differences between past and emerging threat models that apply to LLMs. Using this framework, we illustrate that progress requires disentangling adversarial alignment into addressable sub-problems and returning to core academic principles, such as measureability, reproducibility, and comparability. Although the field presents significant challenges, the fresh start on adversarial robustness offers the unique opportunity to build on past experience while avoiding previous mistakes.

Certifiably Robust Encoding Schemes

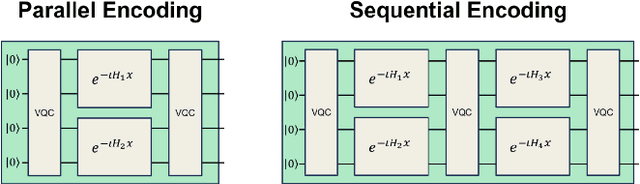
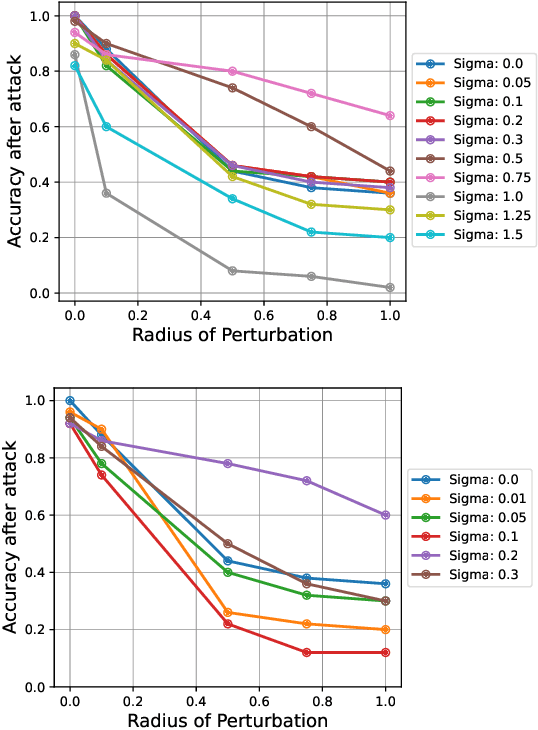
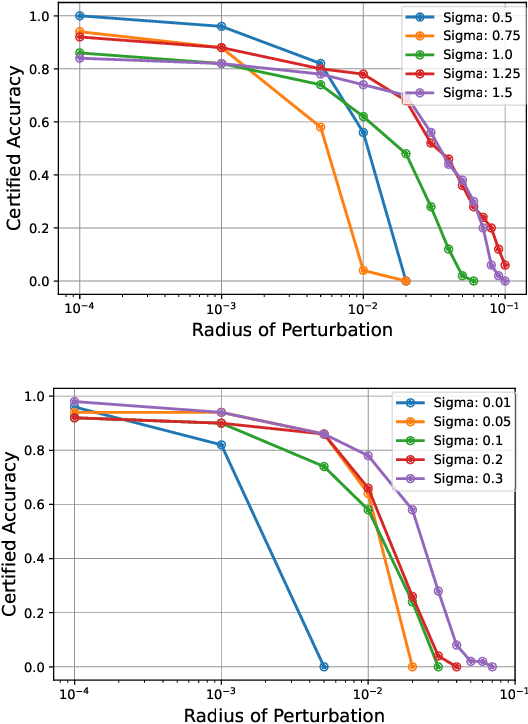
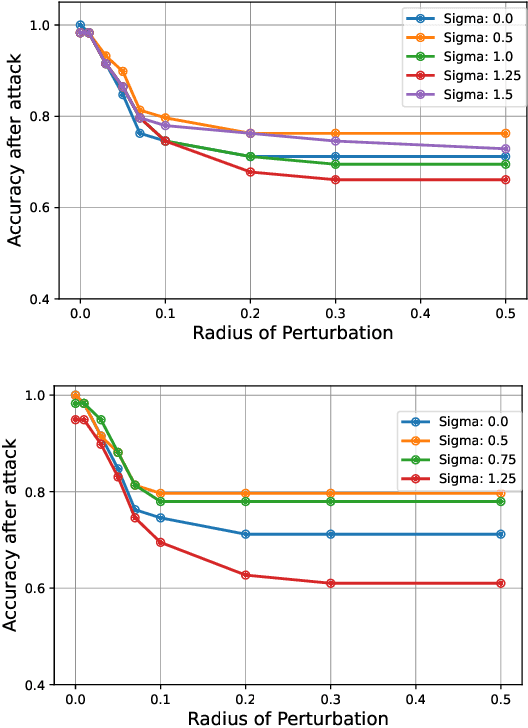
Quantum machine learning uses principles from quantum mechanics to process data, offering potential advances in speed and performance. However, previous work has shown that these models are susceptible to attacks that manipulate input data or exploit noise in quantum circuits. Following this, various studies have explored the robustness of these models. These works focus on the robustness certification of manipulations of the quantum states. We extend this line of research by investigating the robustness against perturbations in the classical data for a general class of data encoding schemes. We show that for such schemes, the addition of suitable noise channels is equivalent to evaluating the mean value of the noiseless classifier at the smoothed data, akin to Randomized Smoothing from classical machine learning. Using our general framework, we show that suitable additions of phase-damping noise channels improve empirical and provable robustness for the considered class of encoding schemes.

Discrete Randomized Smoothing Meets Quantum Computing

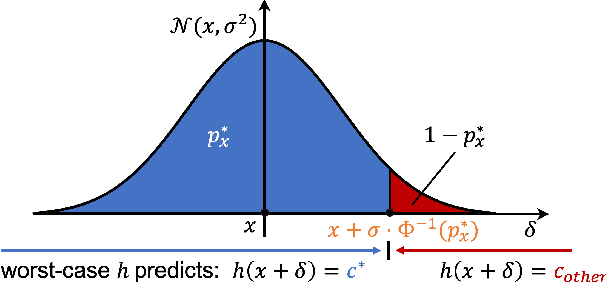
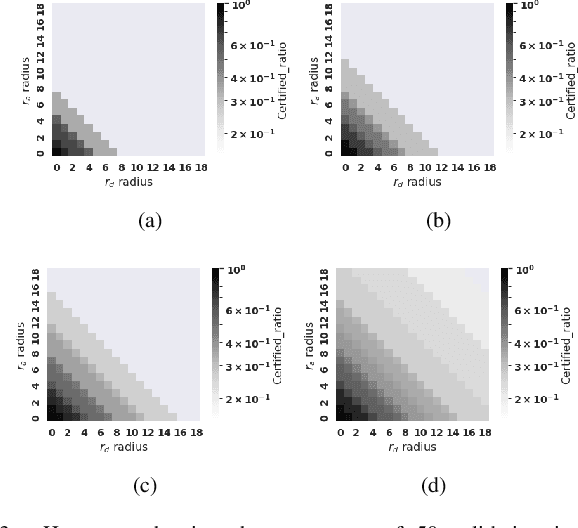
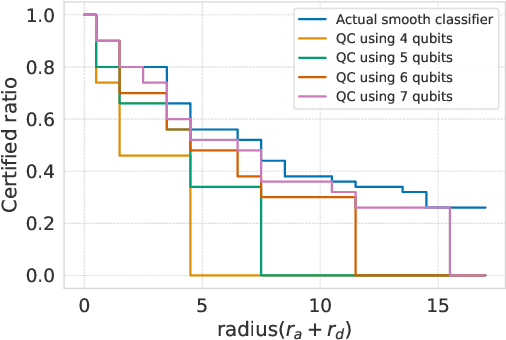
Breakthroughs in machine learning (ML) and advances in quantum computing (QC) drive the interdisciplinary field of quantum machine learning to new levels. However, due to the susceptibility of ML models to adversarial attacks, practical use raises safety-critical concerns. Existing Randomized Smoothing (RS) certification methods for classical machine learning models are computationally intensive. In this paper, we propose the combination of QC and the concept of discrete randomized smoothing to speed up the stochastic certification of ML models for discrete data. We show how to encode all the perturbations of the input binary data in superposition and use Quantum Amplitude Estimation (QAE) to obtain a quadratic reduction in the number of calls to the model that are required compared to traditional randomized smoothing techniques. In addition, we propose a new binary threat model to allow for an extensive evaluation of our approach on images, graphs, and text.

Lift Your Molecules: Molecular Graph Generation in Latent Euclidean Space

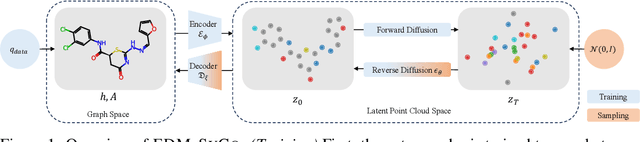
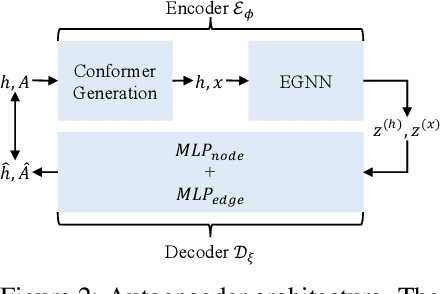
We introduce a new framework for molecular graph generation with 3D molecular generative models. Our Synthetic Coordinate Embedding (SyCo) framework maps molecular graphs to Euclidean point clouds via synthetic conformer coordinates and learns the inverse map using an E(n)-Equivariant Graph Neural Network (EGNN). The induced point cloud-structured latent space is well-suited to apply existing 3D molecular generative models. This approach simplifies the graph generation problem - without relying on molecular fragments nor autoregressive decoding - into a point cloud generation problem followed by node and edge classification tasks. Further, we propose a novel similarity-constrained optimization scheme for 3D diffusion models based on inpainting and guidance. As a concrete implementation of our framework, we develop EDM-SyCo based on the E(3) Equivariant Diffusion Model (EDM). EDM-SyCo achieves state-of-the-art performance in distribution learning of molecular graphs, outperforming the best non-autoregressive methods by more than 30% on ZINC250K and 16% on the large-scale GuacaMol dataset while improving conditional generation by up to 3.9 times.

Expressivity and Generalization: Fragment-Biases for Molecular GNNs

Although recent advances in higher-order Graph Neural Networks (GNNs) improve the theoretical expressiveness and molecular property predictive performance, they often fall short of the empirical performance of models that explicitly use fragment information as inductive bias. However, for these approaches, there exists no theoretic expressivity study. In this work, we propose the Fragment-WL test, an extension to the well-known Weisfeiler & Leman (WL) test, which enables the theoretic analysis of these fragment-biased GNNs. Building on the insights gained from the Fragment-WL test, we develop a new GNN architecture and a fragmentation with infinite vocabulary that significantly boosts expressiveness. We show the effectiveness of our model on synthetic and real-world data where we outperform all GNNs on Peptides and have 12% lower error than all GNNs on ZINC and 34% lower error than other fragment-biased models. Furthermore, we show that our model exhibits superior generalization capabilities compared to the latest transformer-based architectures, positioning it as a robust solution for a range of molecular modeling tasks.

Energy-based Epistemic Uncertainty for Graph Neural Networks

In domains with interdependent data, such as graphs, quantifying the epistemic uncertainty of a Graph Neural Network (GNN) is challenging as uncertainty can arise at different structural scales. Existing techniques neglect this issue or only distinguish between structure-aware and structure-agnostic uncertainty without combining them into a single measure. We propose GEBM, an energy-based model (EBM) that provides high-quality uncertainty estimates by aggregating energy at different structural levels that naturally arise from graph diffusion. In contrast to logit-based EBMs, we provably induce an integrable density in the data space by regularizing the energy function. We introduce an evidential interpretation of our EBM that significantly improves the predictive robustness of the GNN. Our framework is a simple and effective post hoc method applicable to any pre-trained GNN that is sensitive to various distribution shifts. It consistently achieves the best separation of in-distribution and out-of-distribution data on 6 out of 7 anomaly types while having the best average rank over shifts on \emph{all} datasets.

Uncertainty for Active Learning on Graphs

Uncertainty Sampling is an Active Learning strategy that aims to improve the data efficiency of machine learning models by iteratively acquiring labels of data points with the highest uncertainty. While it has proven effective for independent data its applicability to graphs remains under-explored. We propose the first extensive study of Uncertainty Sampling for node classification: (1) We benchmark Uncertainty Sampling beyond predictive uncertainty and highlight a significant performance gap to other Active Learning strategies. (2) We develop ground-truth Bayesian uncertainty estimates in terms of the data generating process and prove their effectiveness in guiding Uncertainty Sampling toward optimal queries. We confirm our results on synthetic data and design an approximate approach that consistently outperforms other uncertainty estimators on real datasets. (3) Based on this analysis, we relate pitfalls in modeling uncertainty to existing methods. Our analysis enables and informs the development of principled uncertainty estimation on graphs.

Attacking Large Language Models with Projected Gradient Descent

Current LLM alignment methods are readily broken through specifically crafted adversarial prompts. While crafting adversarial prompts using discrete optimization is highly effective, such attacks typically use more than 100,000 LLM calls. This high computational cost makes them unsuitable for, e.g., quantitative analyses and adversarial training. To remedy this, we revisit Projected Gradient Descent (PGD) on the continuously relaxed input prompt. Although previous attempts with ordinary gradient-based attacks largely failed, we show that carefully controlling the error introduced by the continuous relaxation tremendously boosts their efficacy. Our PGD for LLMs is up to one order of magnitude faster than state-of-the-art discrete optimization to achieve the same devastating attack results.