Johanna Sommer
Predictive Feature Caching for Training-free Acceleration of Molecular Geometry Generation
Oct 06, 2025Abstract:Flow matching models generate high-fidelity molecular geometries but incur significant computational costs during inference, requiring hundreds of network evaluations. This inference overhead becomes the primary bottleneck when such models are employed in practice to sample large numbers of molecular candidates. This work discusses a training-free caching strategy that accelerates molecular geometry generation by predicting intermediate hidden states across solver steps. The proposed method operates directly on the SE(3)-equivariant backbone, is compatible with pretrained models, and is orthogonal to existing training-based accelerations and system-level optimizations. Experiments on the GEOM-Drugs dataset demonstrate that caching achieves a twofold reduction in wall-clock inference time at matched sample quality and a speedup of up to 3x compared to the base model with minimal sample quality degradation. Because these gains compound with other optimizations, applying caching alongside other general, lossless optimizations yield as much as a 7x speedup.
Unified Guidance for Geometry-Conditioned Molecular Generation
Jan 05, 2025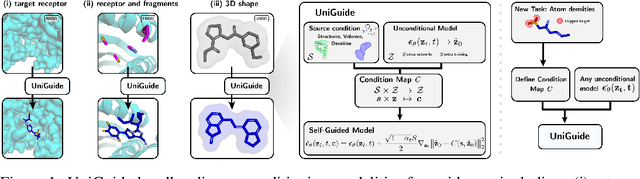
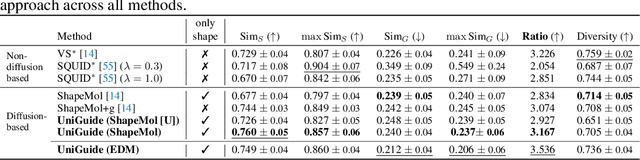
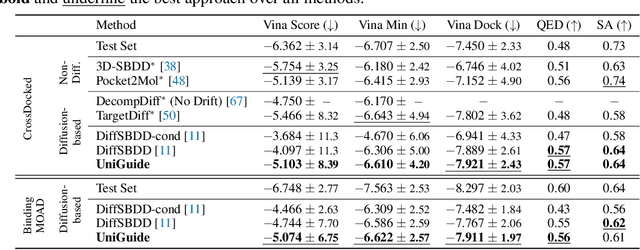
Abstract:Effectively designing molecular geometries is essential to advancing pharmaceutical innovations, a domain, which has experienced great attention through the success of generative models and, in particular, diffusion models. However, current molecular diffusion models are tailored towards a specific downstream task and lack adaptability. We introduce UniGuide, a framework for controlled geometric guidance of unconditional diffusion models that allows flexible conditioning during inference without the requirement of extra training or networks. We show how applications such as structure-based, fragment-based, and ligand-based drug design are formulated in the UniGuide framework and demonstrate on-par or superior performance compared to specialised models. Offering a more versatile approach, UniGuide has the potential to streamline the development of molecular generative models, allowing them to be readily used in diverse application scenarios.
OneProt: Towards Multi-Modal Protein Foundation Models
Nov 07, 2024



Abstract:Recent AI advances have enabled multi-modal systems to model and translate diverse information spaces. Extending beyond text and vision, we introduce OneProt, a multi-modal AI for proteins that integrates structural, sequence, alignment, and binding site data. Using the ImageBind framework, OneProt aligns the latent spaces of modality encoders along protein sequences. It demonstrates strong performance in retrieval tasks and surpasses state-of-the-art methods in various downstream tasks, including metal ion binding classification, gene-ontology annotation, and enzyme function prediction. This work expands multi-modal capabilities in protein models, paving the way for applications in drug discovery, biocatalytic reaction planning, and protein engineering.
Lift Your Molecules: Molecular Graph Generation in Latent Euclidean Space
Jun 15, 2024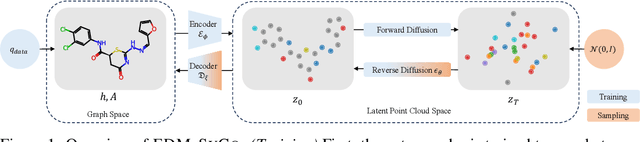

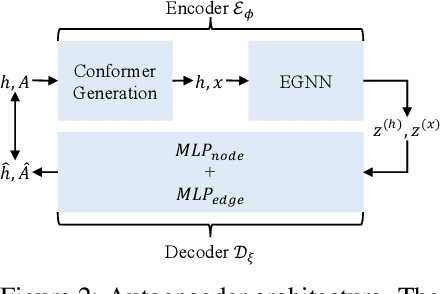

Abstract:We introduce a new framework for molecular graph generation with 3D molecular generative models. Our Synthetic Coordinate Embedding (SyCo) framework maps molecular graphs to Euclidean point clouds via synthetic conformer coordinates and learns the inverse map using an E(n)-Equivariant Graph Neural Network (EGNN). The induced point cloud-structured latent space is well-suited to apply existing 3D molecular generative models. This approach simplifies the graph generation problem - without relying on molecular fragments nor autoregressive decoding - into a point cloud generation problem followed by node and edge classification tasks. Further, we propose a novel similarity-constrained optimization scheme for 3D diffusion models based on inpainting and guidance. As a concrete implementation of our framework, we develop EDM-SyCo based on the E(3) Equivariant Diffusion Model (EDM). EDM-SyCo achieves state-of-the-art performance in distribution learning of molecular graphs, outperforming the best non-autoregressive methods by more than 30% on ZINC250K and 16% on the large-scale GuacaMol dataset while improving conditional generation by up to 3.9 times.
Expressivity and Generalization: Fragment-Biases for Molecular GNNs
Jun 12, 2024Abstract:Although recent advances in higher-order Graph Neural Networks (GNNs) improve the theoretical expressiveness and molecular property predictive performance, they often fall short of the empirical performance of models that explicitly use fragment information as inductive bias. However, for these approaches, there exists no theoretic expressivity study. In this work, we propose the Fragment-WL test, an extension to the well-known Weisfeiler & Leman (WL) test, which enables the theoretic analysis of these fragment-biased GNNs. Building on the insights gained from the Fragment-WL test, we develop a new GNN architecture and a fragmentation with infinite vocabulary that significantly boosts expressiveness. We show the effectiveness of our model on synthetic and real-world data where we outperform all GNNs on Peptides and have 12% lower error than all GNNs on ZINC and 34% lower error than other fragment-biased models. Furthermore, we show that our model exhibits superior generalization capabilities compared to the latest transformer-based architectures, positioning it as a robust solution for a range of molecular modeling tasks.
MAGNet: Motif-Agnostic Generation of Molecules from Shapes
May 30, 2023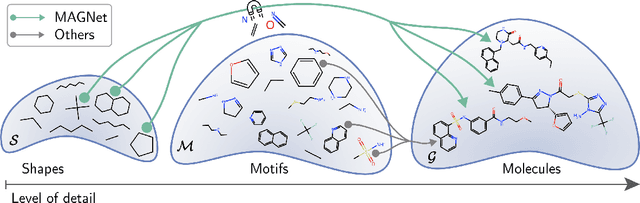
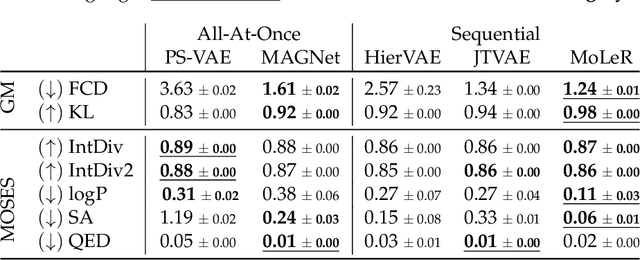
Abstract:Recent advances in machine learning for molecules exhibit great potential for facilitating drug discovery from in silico predictions. Most models for molecule generation rely on the decomposition of molecules into frequently occurring substructures (motifs), from which they generate novel compounds. While motif representations greatly aid in learning molecular distributions, such methods struggle to represent substructures beyond their known motif set. To alleviate this issue and increase flexibility across datasets, we propose MAGNet, a graph-based model that generates abstract shapes before allocating atom and bond types. To this end, we introduce a novel factorisation of the molecules' data distribution that accounts for the molecules' global context and facilitates learning adequate assignments of atoms and bonds onto shapes. While the abstraction to shapes introduces greater complexity for distribution learning, we show the competitive performance of MAGNet on standard benchmarks. Importantly, we demonstrate that MAGNet's improved expressivity leads to molecules with more topologically distinct structures and, at the same time, diverse atom and bond assignments.
Neural Flows: Efficient Alternative to Neural ODEs
Oct 25, 2021
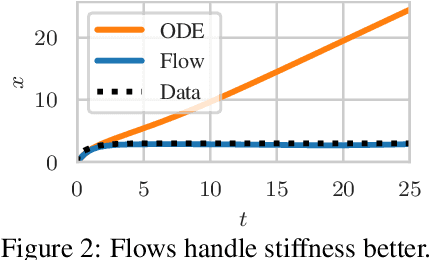
Abstract:Neural ordinary differential equations describe how values change in time. This is the reason why they gained importance in modeling sequential data, especially when the observations are made at irregular intervals. In this paper we propose an alternative by directly modeling the solution curves - the flow of an ODE - with a neural network. This immediately eliminates the need for expensive numerical solvers while still maintaining the modeling capability of neural ODEs. We propose several flow architectures suitable for different applications by establishing precise conditions on when a function defines a valid flow. Apart from computational efficiency, we also provide empirical evidence of favorable generalization performance via applications in time series modeling, forecasting, and density estimation.
Generalization of Neural Combinatorial Solvers Through the Lens of Adversarial Robustness
Oct 21, 2021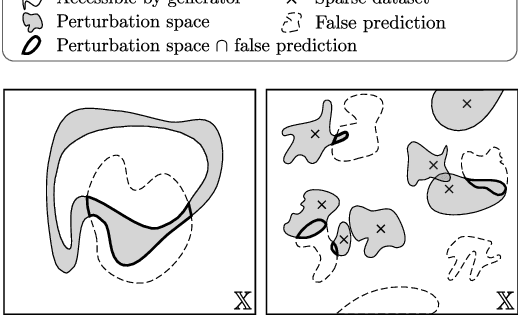
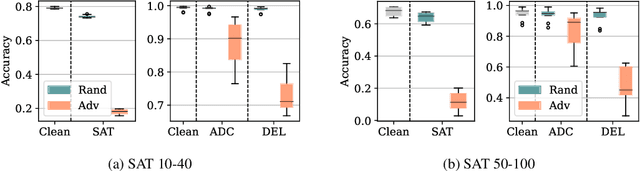
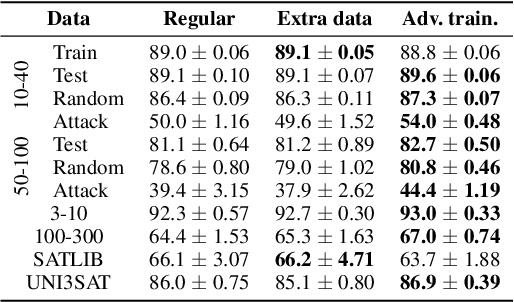
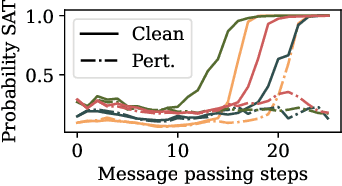
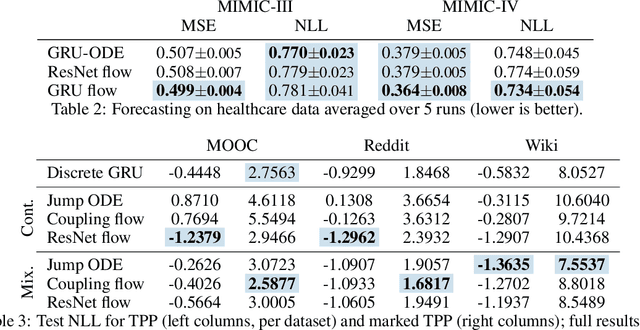
Abstract:End-to-end (geometric) deep learning has seen first successes in approximating the solution of combinatorial optimization problems. However, generating data in the realm of NP-hard/-complete tasks brings practical and theoretical challenges, resulting in evaluation protocols that are too optimistic. Specifically, most datasets only capture a simpler subproblem and likely suffer from spurious features. We investigate these effects by studying adversarial robustness - a local generalization property - to reveal hard, model-specific instances and spurious features. For this purpose, we derive perturbation models for SAT and TSP. Unlike in other applications, where perturbation models are designed around subjective notions of imperceptibility, our perturbation models are efficient and sound, allowing us to determine the true label of perturbed samples without a solver. Surprisingly, with such perturbations, a sufficiently expressive neural solver does not suffer from the limitations of the accuracy-robustness trade-off common in supervised learning. Although such robust solvers exist, we show empirically that the assessed neural solvers do not generalize well w.r.t. small perturbations of the problem instance.
Learning to Tune XGBoost with XGBoost
Sep 19, 2019


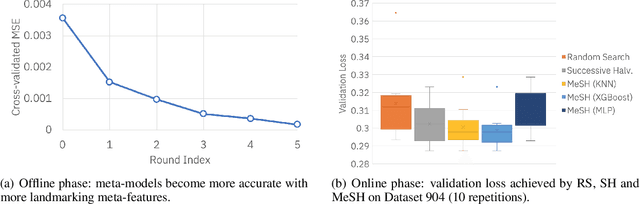
Abstract:In this short paper we investigate whether meta-learning techniques can be used to more effectively tune the hyperparameters of machine learning models using successive halving (SH). We propose a novel variant of the SH algorithm (MeSH), that uses meta-regressors to determine which candidate configurations should be eliminated at each round. We apply MeSH to the problem of tuning the hyperparameters of a gradient-boosted decision tree model. By training and tuning our meta-regressors using existing tuning jobs from 95 datasets, we demonstrate that MeSH can often find a superior solution to both SH and random search.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge