Learning to Tune XGBoost with XGBoost
Paper and Code
Sep 19, 2019


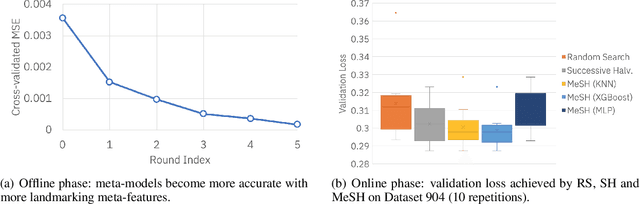
In this short paper we investigate whether meta-learning techniques can be used to more effectively tune the hyperparameters of machine learning models using successive halving (SH). We propose a novel variant of the SH algorithm (MeSH), that uses meta-regressors to determine which candidate configurations should be eliminated at each round. We apply MeSH to the problem of tuning the hyperparameters of a gradient-boosted decision tree model. By training and tuning our meta-regressors using existing tuning jobs from 95 datasets, we demonstrate that MeSH can often find a superior solution to both SH and random search.
* 5 pages (references included)
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge