Privacy Amplification by Structured Subsampling for Deep Differentially Private Time Series Forecasting

Many forms of sensitive data, such as web traffic, mobility data, or hospital occupancy, are inherently sequential. The standard method for training machine learning models while ensuring privacy for units of sensitive information, such as individual hospital visits, is differentially private stochastic gradient descent (DP-SGD). However, we observe in this work that the formal guarantees of DP-SGD are incompatible with timeseries-specific tasks like forecasting, since they rely on the privacy amplification attained by training on small, unstructured batches sampled from an unstructured dataset. In contrast, batches for forecasting are generated by (1) sampling sequentially structured time series from a dataset, (2) sampling contiguous subsequences from these series, and (3) partitioning them into context and ground-truth forecast windows. We theoretically analyze the privacy amplification attained by this structured subsampling to enable the training of forecasting models with sound and tight event- and user-level privacy guarantees. Towards more private models, we additionally prove how data augmentation amplifies privacy in self-supervised training of sequence models. Our empirical evaluation demonstrates that amplification by structured subsampling enables the training of forecasting models with strong formal privacy guarantees.

Group Privacy Amplification and Unified Amplification by Subsampling for Rényi Differential Privacy

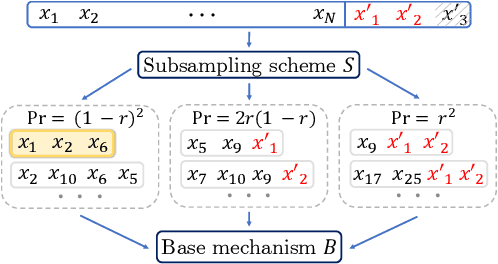
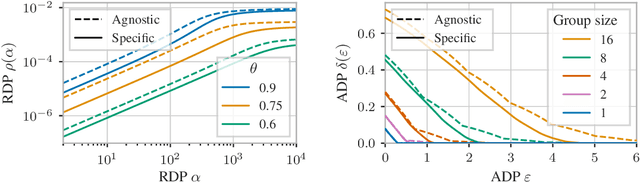
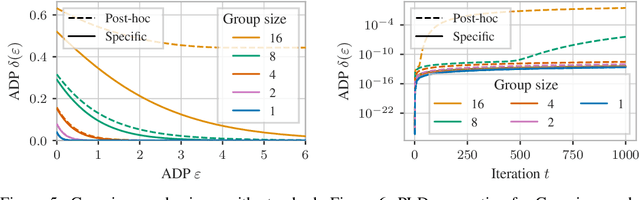
Differential privacy (DP) has various desirable properties, such as robustness to post-processing, group privacy, and amplification by subsampling, which can be derived independently of each other. Our goal is to determine whether stronger privacy guarantees can be obtained by considering multiple of these properties jointly. To this end, we focus on the combination of group privacy and amplification by subsampling. To provide guarantees that are amenable to machine learning algorithms, we conduct our analysis in the framework of R\'enyi-DP, which has more favorable composition properties than $(\epsilon,\delta)$-DP. As part of this analysis, we develop a unified framework for deriving amplification by subsampling guarantees for R\'enyi-DP, which represents the first such framework for a privacy accounting method and is of independent interest. We find that it not only lets us improve upon and generalize existing amplification results for R\'enyi-DP, but also derive provably tight group privacy amplification guarantees stronger than existing principles. These results establish the joint study of different DP properties as a promising research direction.

(Provable) Adversarial Robustness for Group Equivariant Tasks: Graphs, Point Clouds, Molecules, and More

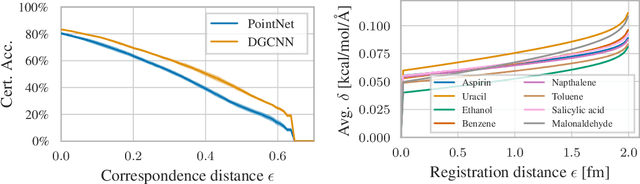
A machine learning model is traditionally considered robust if its prediction remains (almost) constant under input perturbations with small norm. However, real-world tasks like molecular property prediction or point cloud segmentation have inherent equivariances, such as rotation or permutation equivariance. In such tasks, even perturbations with large norm do not necessarily change an input's semantic content. Furthermore, there are perturbations for which a model's prediction explicitly needs to change. For the first time, we propose a sound notion of adversarial robustness that accounts for task equivariance. We then demonstrate that provable robustness can be achieved by (1) choosing a model that matches the task's equivariances (2) certifying traditional adversarial robustness. Certification methods are, however, unavailable for many models, such as those with continuous equivariances. We close this gap by developing the framework of equivariance-preserving randomized smoothing, which enables architecture-agnostic certification. We additionally derive the first architecture-specific graph edit distance certificates, i.e. sound robustness guarantees for isomorphism equivariant tasks like node classification. Overall, a sound notion of robustness is an important prerequisite for future work at the intersection of robust and geometric machine learning.

Hierarchical Randomized Smoothing

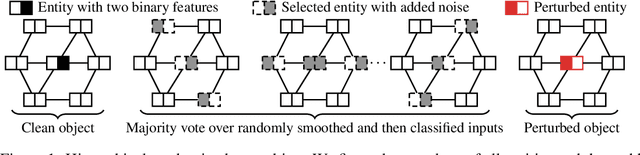
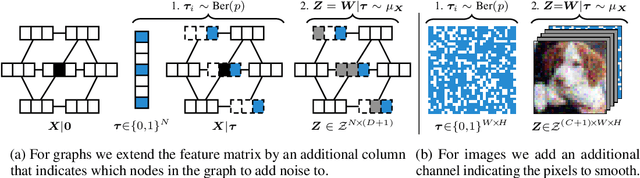
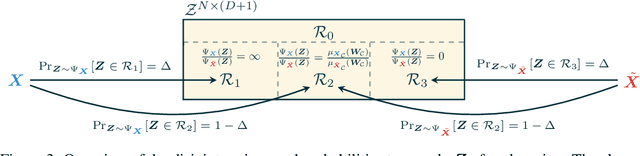
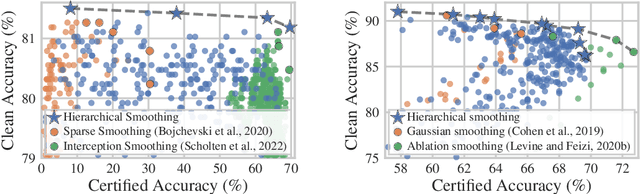
Real-world data is complex and often consists of objects that can be decomposed into multiple entities (e.g. images into pixels, graphs into interconnected nodes). Randomized smoothing is a powerful framework for making models provably robust against small changes to their inputs - by guaranteeing robustness of the majority vote when randomly adding noise before classification. Yet, certifying robustness on such complex data via randomized smoothing is challenging when adversaries do not arbitrarily perturb entire objects (e.g. images) but only a subset of their entities (e.g. pixels). As a solution, we introduce hierarchical randomized smoothing: We partially smooth objects by adding random noise only on a randomly selected subset of their entities. By adding noise in a more targeted manner than existing methods we obtain stronger robustness guarantees while maintaining high accuracy. We initialize hierarchical smoothing using different noising distributions, yielding novel robustness certificates for discrete and continuous domains. We experimentally demonstrate the importance of hierarchical smoothing in image and node classification, where it yields superior robustness-accuracy trade-offs. Overall, hierarchical smoothing is an important contribution towards models that are both - certifiably robust to perturbations and accurate.

Collective Robustness Certificates: Exploiting Interdependence in Graph Neural Networks

In tasks like node classification, image segmentation, and named-entity recognition we have a classifier that simultaneously outputs multiple predictions (a vector of labels) based on a single input, i.e. a single graph, image, or document respectively. Existing adversarial robustness certificates consider each prediction independently and are thus overly pessimistic for such tasks. They implicitly assume that an adversary can use different perturbed inputs to attack different predictions, ignoring the fact that we have a single shared input. We propose the first collective robustness certificate which computes the number of predictions that are simultaneously guaranteed to remain stable under perturbation, i.e. cannot be attacked. We focus on Graph Neural Networks and leverage their locality property - perturbations only affect the predictions in a close neighborhood - to fuse multiple single-node certificates into a drastically stronger collective certificate. For example, on the Citeseer dataset our collective certificate for node classification increases the average number of certifiable feature perturbations from $7$ to $351$.

Randomized Message-Interception Smoothing: Gray-box Certificates for Graph Neural Networks

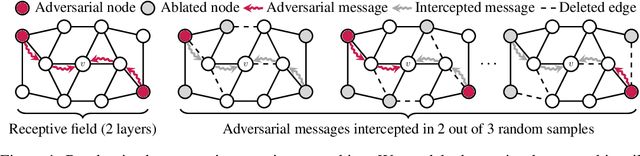
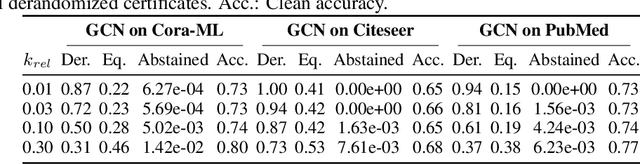
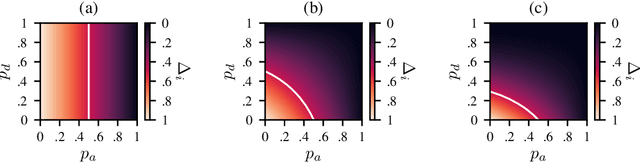
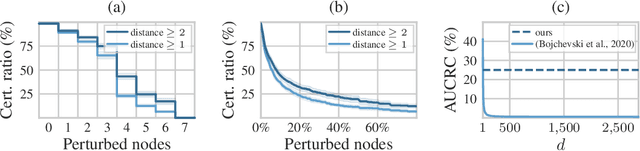
Randomized smoothing is one of the most promising frameworks for certifying the adversarial robustness of machine learning models, including Graph Neural Networks (GNNs). Yet, existing randomized smoothing certificates for GNNs are overly pessimistic since they treat the model as a black box, ignoring the underlying architecture. To remedy this, we propose novel gray-box certificates that exploit the message-passing principle of GNNs: We randomly intercept messages and carefully analyze the probability that messages from adversarially controlled nodes reach their target nodes. Compared to existing certificates, we certify robustness to much stronger adversaries that control entire nodes in the graph and can arbitrarily manipulate node features. Our certificates provide stronger guarantees for attacks at larger distances, as messages from farther-away nodes are more likely to get intercepted. We demonstrate the effectiveness of our method on various models and datasets. Since our gray-box certificates consider the underlying graph structure, we can significantly improve certifiable robustness by applying graph sparsification.

Training Differentially Private Graph Neural Networks with Random Walk Sampling

Deep learning models are known to put the privacy of their training data at risk, which poses challenges for their safe and ethical release to the public. Differentially private stochastic gradient descent is the de facto standard for training neural networks without leaking sensitive information about the training data. However, applying it to models for graph-structured data poses a novel challenge: unlike with i.i.d. data, sensitive information about a node in a graph cannot only leak through its gradients, but also through the gradients of all nodes within a larger neighborhood. In practice, this limits privacy-preserving deep learning on graphs to very shallow graph neural networks. We propose to solve this issue by training graph neural networks on disjoint subgraphs of a given training graph. We develop three random-walk-based methods for generating such disjoint subgraphs and perform a careful analysis of the data-generating distributions to provide strong privacy guarantees. Through extensive experiments, we show that our method greatly outperforms the state-of-the-art baseline on three large graphs, and matches or outperforms it on four smaller ones.

Invariance-Aware Randomized Smoothing Certificates

Building models that comply with the invariances inherent to different domains, such as invariance under translation or rotation, is a key aspect of applying machine learning to real world problems like molecular property prediction, medical imaging, protein folding or LiDAR classification. For the first time, we study how the invariances of a model can be leveraged to provably guarantee the robustness of its predictions. We propose a gray-box approach, enhancing the powerful black-box randomized smoothing technique with white-box knowledge about invariances. First, we develop gray-box certificates based on group orbits, which can be applied to arbitrary models with invariance under permutation and Euclidean isometries. Then, we derive provably tight gray-box certificates. We experimentally demonstrate that the provably tight certificates can offer much stronger guarantees, but that in practical scenarios the orbit-based method is a good approximation.

Localized Randomized Smoothing for Collective Robustness Certification

Models for image segmentation, node classification and many other tasks map a single input to multiple labels. By perturbing this single shared input (e.g. the image) an adversary can manipulate several predictions (e.g. misclassify several pixels). Collective robustness certification is the task of provably bounding the number of robust predictions under this threat model. The only dedicated method that goes beyond certifying each output independently is limited to strictly local models, where each prediction is associated with a small receptive field. We propose a more general collective robustness certificate for all types of models and further show that this approach is beneficial for the larger class of softly local models, where each output is dependent on the entire input but assigns different levels of importance to different input regions (e.g. based on their proximity in the image). The certificate is based on our novel localized randomized smoothing approach, where the random perturbation strength for different input regions is proportional to their importance for the outputs. Localized smoothing Pareto-dominates existing certificates on both image segmentation and node classification tasks, simultaneously offering higher accuracy and stronger guarantees.

Generalization of Neural Combinatorial Solvers Through the Lens of Adversarial Robustness

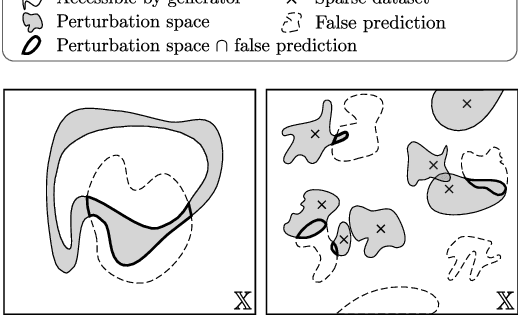
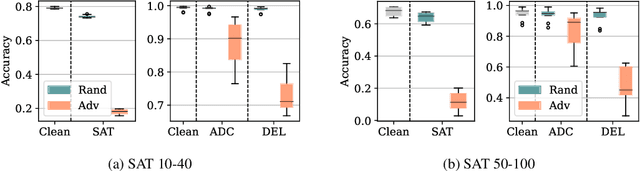
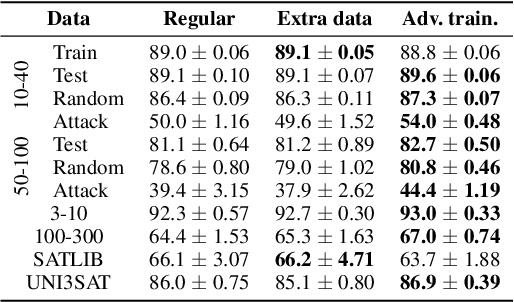
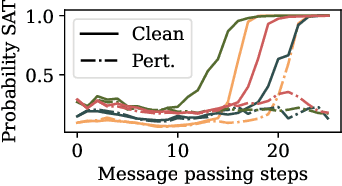
End-to-end (geometric) deep learning has seen first successes in approximating the solution of combinatorial optimization problems. However, generating data in the realm of NP-hard/-complete tasks brings practical and theoretical challenges, resulting in evaluation protocols that are too optimistic. Specifically, most datasets only capture a simpler subproblem and likely suffer from spurious features. We investigate these effects by studying adversarial robustness - a local generalization property - to reveal hard, model-specific instances and spurious features. For this purpose, we derive perturbation models for SAT and TSP. Unlike in other applications, where perturbation models are designed around subjective notions of imperceptibility, our perturbation models are efficient and sound, allowing us to determine the true label of perturbed samples without a solver. Surprisingly, with such perturbations, a sufficiently expressive neural solver does not suffer from the limitations of the accuracy-robustness trade-off common in supervised learning. Although such robust solvers exist, we show empirically that the assessed neural solvers do not generalize well w.r.t. small perturbations of the problem instance.