Optimal Conformal Prediction under Epistemic Uncertainty

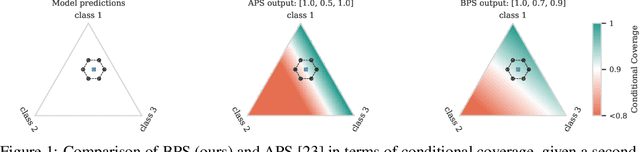
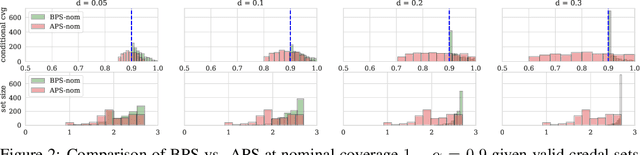
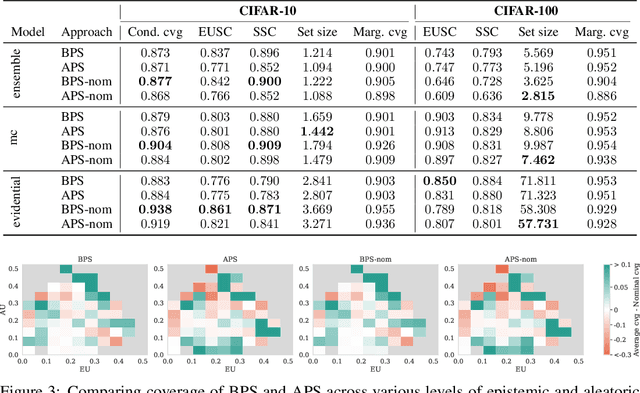
Conformal prediction (CP) is a popular frequentist framework for representing uncertainty by providing prediction sets that guarantee coverage of the true label with a user-adjustable probability. In most applications, CP operates on confidence scores coming from a standard (first-order) probabilistic predictor (e.g., softmax outputs). Second-order predictors, such as credal set predictors or Bayesian models, are also widely used for uncertainty quantification and are known for their ability to represent both aleatoric and epistemic uncertainty. Despite their popularity, there is still an open question on ``how they can be incorporated into CP''. In this paper, we discuss the desiderata for CP when valid second-order predictions are available. We then introduce Bernoulli prediction sets (BPS), which produce the smallest prediction sets that ensure conditional coverage in this setting. When given first-order predictions, BPS reduces to the well-known adaptive prediction sets (APS). Furthermore, when the validity assumption on the second-order predictions is compromised, we apply conformal risk control to obtain a marginal coverage guarantee while still accounting for epistemic uncertainty.

Robust Conformal Prediction with a Single Binary Certificate

Conformal prediction (CP) converts any model's output to prediction sets with a guarantee to cover the true label with (adjustable) high probability. Robust CP extends this guarantee to worst-case (adversarial) inputs. Existing baselines achieve robustness by bounding randomly smoothed conformity scores. In practice, they need expensive Monte-Carlo (MC) sampling (e.g. $\sim10^4$ samples per point) to maintain an acceptable set size. We propose a robust conformal prediction that produces smaller sets even with significantly lower MC samples (e.g. 150 for CIFAR10). Our approach binarizes samples with an adjustable (or automatically adjusted) threshold selected to preserve the coverage guarantee. Remarkably, we prove that robustness can be achieved by computing only one binary certificate, unlike previous methods that certify each calibration (or test) point. Thus, our method is faster and returns smaller robust sets. We also eliminate a previous limitation that requires a bounded score function.

KurTail : Kurtosis-based LLM Quantization

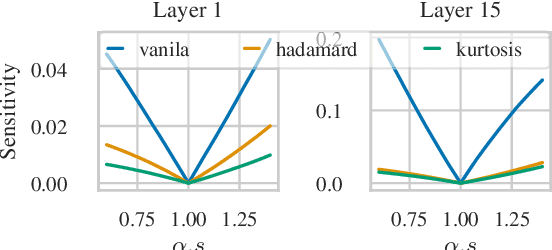
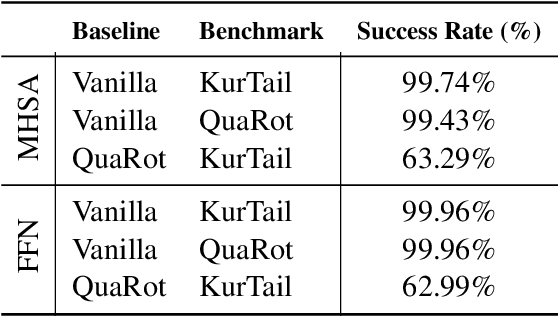
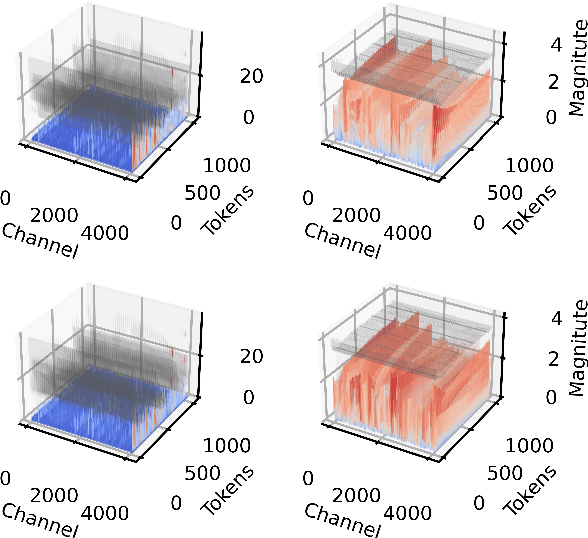
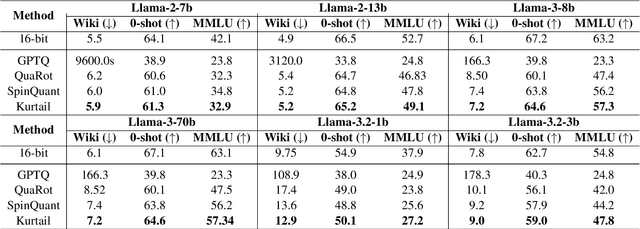
One of the challenges of quantizing a large language model (LLM) is the presence of outliers. Outliers often make uniform quantization schemes less effective, particularly in extreme cases such as 4-bit quantization. We introduce KurTail, a new post-training quantization (PTQ) scheme that leverages Kurtosis-based rotation to mitigate outliers in the activations of LLMs. Our method optimizes Kurtosis as a measure of tailedness. This approach enables the quantization of weights, activations, and the KV cache in 4 bits. We utilize layer-wise optimization, ensuring memory efficiency. KurTail outperforms existing quantization methods, offering a 13.3\% boost in MMLU accuracy and a 15.5\% drop in Wiki perplexity compared to QuaRot. It also outperforms SpinQuant with a 2.6\% MMLU gain and reduces perplexity by 2.9\%, all while reducing the training cost. For comparison, learning the rotation using SpinQuant for Llama3-70B requires at least four NVIDIA H100 80GB GPUs, whereas our method requires only a single GPU, making it a more accessible solution for consumer GPU.

SafePowerGraph: Safety-aware Evaluation of Graph Neural Networks for Transmission Power Grids

Power grids are critical infrastructures of paramount importance to modern society and their rapid evolution and interconnections has heightened the complexity of power systems (PS) operations. Traditional methods for grid analysis struggle with the computational demands of large-scale RES and ES integration, prompting the adoption of machine learning (ML) techniques, particularly Graph Neural Networks (GNNs). GNNs have proven effective in solving the alternating current (AC) Power Flow (PF) and Optimal Power Flow (OPF) problems, crucial for operational planning. However, existing benchmarks and datasets completely ignore safety and robustness requirements in their evaluation and never consider realistic safety-critical scenarios that most impact the operations of the power grids. We present SafePowerGraph, the first simulator-agnostic, safety-oriented framework and benchmark for GNNs in PS operations. SafePowerGraph integrates multiple PF and OPF simulators and assesses GNN performance under diverse scenarios, including energy price variations and power line outages. Our extensive experiments underscore the importance of self-supervised learning and graph attention architectures for GNN robustness. We provide at https://github.com/yamizi/SafePowerGraph our open-source repository, a comprehensive leaderboard, a dataset and model zoo and expect our framework to standardize and advance research in the critical field of GNN for power systems.

Robust Yet Efficient Conformal Prediction Sets

Conformal prediction (CP) can convert any model's output into prediction sets guaranteed to include the true label with any user-specified probability. However, same as the model itself, CP is vulnerable to adversarial test examples (evasion) and perturbed calibration data (poisoning). We derive provably robust sets by bounding the worst-case change in conformity scores. Our tighter bounds lead to more efficient sets. We cover both continuous and discrete (sparse) data and our guarantees work both for evasion and poisoning attacks (on both features and labels).

Conformal Inductive Graph Neural Networks

Conformal prediction (CP) transforms any model's output into prediction sets guaranteed to include (cover) the true label. CP requires exchangeability, a relaxation of the i.i.d. assumption, to obtain a valid distribution-free coverage guarantee. This makes it directly applicable to transductive node-classification. However, conventional CP cannot be applied in inductive settings due to the implicit shift in the (calibration) scores caused by message passing with the new nodes. We fix this issue for both cases of node and edge-exchangeable graphs, recovering the standard coverage guarantee without sacrificing statistical efficiency. We further prove that the guarantee holds independently of the prediction time, e.g. upon arrival of a new node/edge or at any subsequent moment.

SVFT: Parameter-Efficient Fine-Tuning with Singular Vectors

Popular parameter-efficient fine-tuning (PEFT) methods, such as LoRA and its variants, freeze pre-trained model weights \(W\) and inject learnable matrices \(\Delta W\). These \(\Delta W\) matrices are structured for efficient parameterization, often using techniques like low-rank approximations or scaling vectors. However, these methods typically show a performance gap compared to full fine-tuning. Although recent PEFT methods have narrowed this gap, they do so at the cost of additional learnable parameters. We propose SVFT, a simple approach that fundamentally differs from existing methods: the structure imposed on \(\Delta W\) depends on the specific weight matrix \(W\). Specifically, SVFT updates \(W\) as a sparse combination of outer products of its singular vectors, training only the coefficients (scales) of these sparse combinations. This approach allows fine-grained control over expressivity through the number of coefficients. Extensive experiments on language and vision benchmarks show that SVFT recovers up to 96% of full fine-tuning performance while training only 0.006 to 0.25% of parameters, outperforming existing methods that only recover up to 85% performance using 0.03 to 0.8% of the trainable parameter budget.

Are GATs Out of Balance?

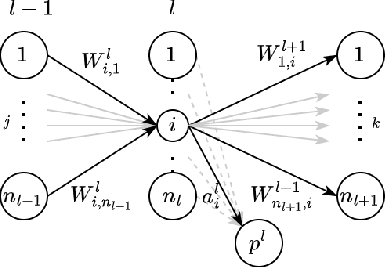
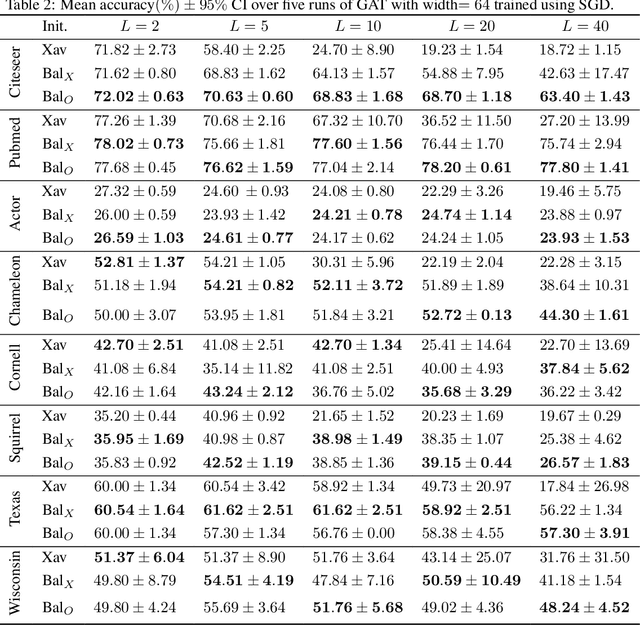
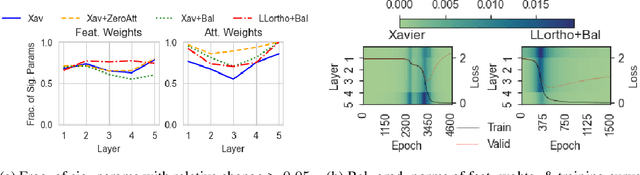
While the expressive power and computational capabilities of graph neural networks (GNNs) have been theoretically studied, their optimization and learning dynamics, in general, remain largely unexplored. Our study undertakes the Graph Attention Network (GAT), a popular GNN architecture in which a node's neighborhood aggregation is weighted by parameterized attention coefficients. We derive a conservation law of GAT gradient flow dynamics, which explains why a high portion of parameters in GATs with standard initialization struggle to change during training. This effect is amplified in deeper GATs, which perform significantly worse than their shallow counterparts. To alleviate this problem, we devise an initialization scheme that balances the GAT network. Our approach i) allows more effective propagation of gradients and in turn enables trainability of deeper networks, and ii) attains a considerable speedup in training and convergence time in comparison to the standard initialization. Our main theorem serves as a stepping stone to studying the learning dynamics of positive homogeneous models with attention mechanisms.

Hierarchical Randomized Smoothing

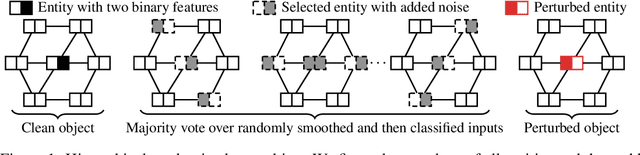
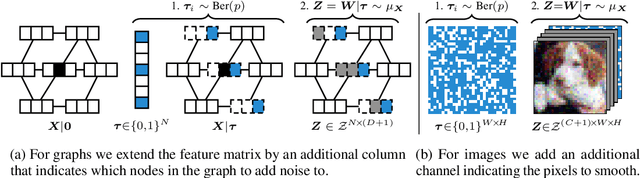
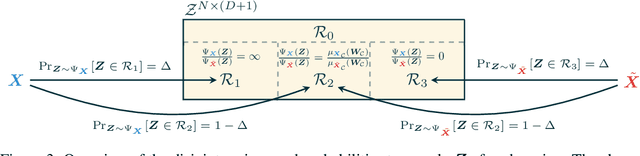
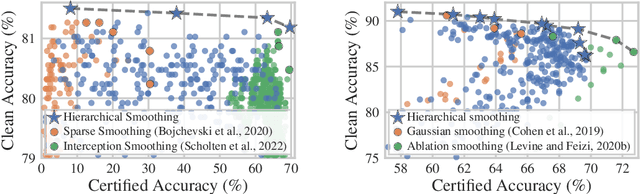
Real-world data is complex and often consists of objects that can be decomposed into multiple entities (e.g. images into pixels, graphs into interconnected nodes). Randomized smoothing is a powerful framework for making models provably robust against small changes to their inputs - by guaranteeing robustness of the majority vote when randomly adding noise before classification. Yet, certifying robustness on such complex data via randomized smoothing is challenging when adversaries do not arbitrarily perturb entire objects (e.g. images) but only a subset of their entities (e.g. pixels). As a solution, we introduce hierarchical randomized smoothing: We partially smooth objects by adding random noise only on a randomly selected subset of their entities. By adding noise in a more targeted manner than existing methods we obtain stronger robustness guarantees while maintaining high accuracy. We initialize hierarchical smoothing using different noising distributions, yielding novel robustness certificates for discrete and continuous domains. We experimentally demonstrate the importance of hierarchical smoothing in image and node classification, where it yields superior robustness-accuracy trade-offs. Overall, hierarchical smoothing is an important contribution towards models that are both - certifiably robust to perturbations and accurate.

Probing Graph Representations

Today we have a good theoretical understanding of the representational power of Graph Neural Networks (GNNs). For example, their limitations have been characterized in relation to a hierarchy of Weisfeiler-Lehman (WL) isomorphism tests. However, we do not know what is encoded in the learned representations. This is our main question. We answer it using a probing framework to quantify the amount of meaningful information captured in graph representations. Our findings on molecular datasets show the potential of probing for understanding the inductive biases of graph-based models. We compare different families of models and show that transformer-based models capture more chemically relevant information compared to models based on message passing. We also study the effect of different design choices such as skip connections and virtual nodes. We advocate for probing as a useful diagnostic tool for evaluating graph-based models.