GeoNorm: Unify Pre-Norm and Post-Norm with Geodesic Optimization

The placement of normalization layers, specifically Pre-Norm and Post-Norm, remains an open question in Transformer architecture design. In this work, we rethink these approaches through the lens of manifold optimization, interpreting the outputs of the Feed-Forward Network (FFN) and attention layers as update directions in optimization. Building on this perspective, we introduce GeoNorm, a novel method that replaces standard normalization with geodesic updates on the manifold. Furthermore, analogous to learning rate schedules, we propose a layer-wise update decay for the FFN and attention components. Comprehensive experiments demonstrate that GeoNorm consistently outperforms existing normalization methods in Transformer models. Crucially, GeoNorm can be seamlessly integrated into standard Transformer architectures, achieving performance improvements with negligible additional computational cost.

AHA: Aligning Large Audio-Language Models for Reasoning Hallucinations via Counterfactual Hard Negatives

Although Large Audio-Language Models (LALMs) deliver state-of-the-art (SOTA) performance, they frequently suffer from hallucinations, e.g. generating text not grounded in the audio input. We analyze these grounding failures and identify a distinct taxonomy: Event Omission, False Event Identity, Temporal Relation Error, and Quantitative Temporal Error. To address this, we introduce the AHA (Audio Hallucination Alignment) framework. By leveraging counterfactual hard negative mining, our pipeline constructs a high-quality preference dataset that forces models to distinguish strict acoustic evidence from linguistically plausible fabrications. Additionally, we establish AHA-Eval, a diagnostic benchmark designed to rigorously test these fine-grained temporal reasoning capabilities. We apply this data to align Qwen2.5-Omni. The resulting model, Qwen-Audio-AHA, achieves a 13.7% improvement on AHA-Eval. Crucially, this benefit generalizes beyond our diagnostic set. Our model shows substantial gains on public benchmarks, including 1.3% on MMAU-Test and 1.6% on MMAR, outperforming latest SOTA methods.

Small Vocabularies, Big Gains: Pretraining and Tokenization in Time Series Models

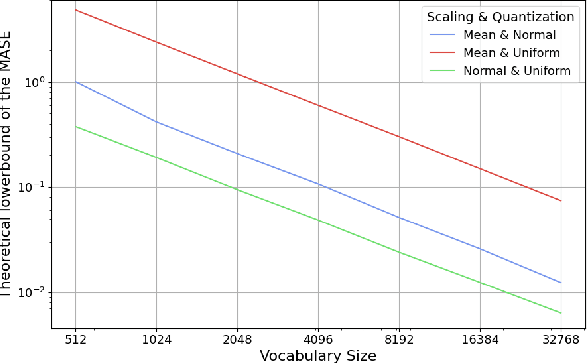
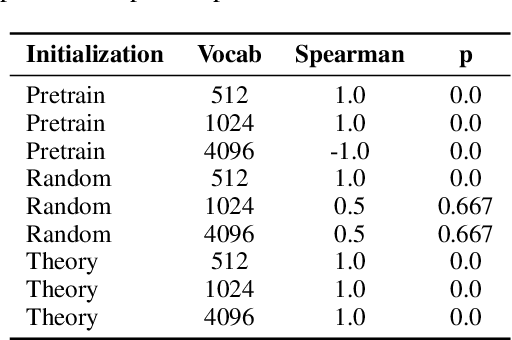
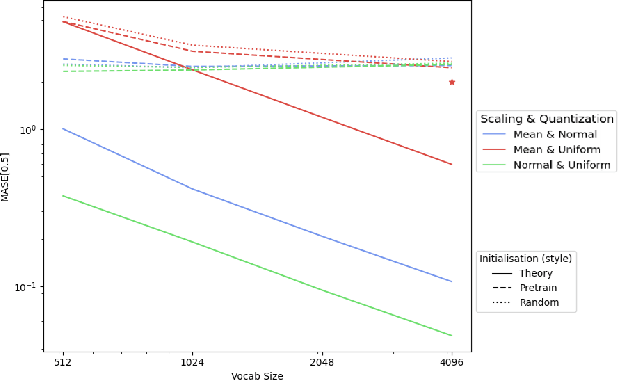
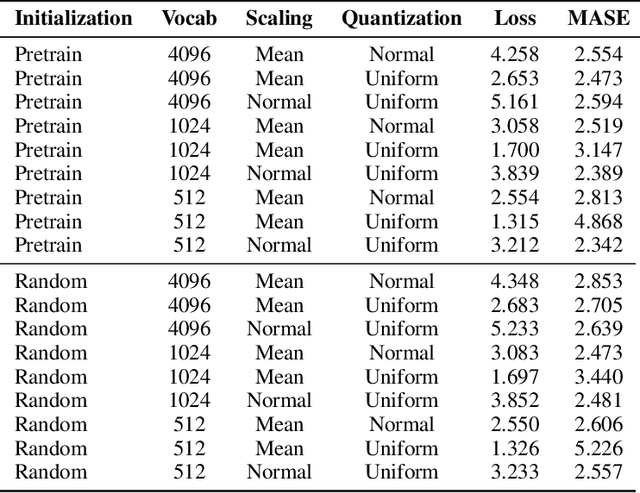
Tokenization and transfer learning are two critical components in building state of the art time series foundation models for forecasting. In this work, we systematically study the effect of tokenizer design, specifically scaling and quantization strategies, on model performance, alongside the impact of pretraining versus random initialization. We show that tokenizer configuration primarily governs the representational capacity and stability of the model, while transfer learning influences optimization efficiency and alignment. Using a combination of empirical training experiments and theoretical analyses, we demonstrate that pretrained models consistently leverage well-designed tokenizers more effectively, particularly at smaller vocabulary sizes. Conversely, misaligned tokenization can diminish or even invert the benefits of pretraining. These findings highlight the importance of careful tokenization in time series modeling and suggest that combining small, efficient vocabularies with pretrained weights is especially advantageous in multi-modal forecasting settings, where the overall vocabulary must be shared across modalities. Our results provide concrete guidance for designing tokenizers and leveraging transfer learning in discrete representation learning for continuous signals.

Reinforcing Multi-Turn Reasoning in LLM Agents via Turn-Level Credit Assignment

This paper investigates approaches to enhance the reasoning capabilities of Large Language Model (LLM) agents using Reinforcement Learning (RL). Specifically, we focus on multi-turn tool-use scenarios, which can be naturally modeled as Markov Decision Processes (MDPs). While existing approaches often train multi-turn LLM agents with trajectory-level advantage estimation in bandit settings, they struggle with turn-level credit assignment across multiple decision steps, limiting their performance on multi-turn reasoning tasks. To address this, we introduce a fine-grained turn-level advantage estimation strategy to enable more precise credit assignment in multi-turn agent interactions. The strategy is general and can be incorporated into various RL algorithms such as Group Relative Preference Optimization (GRPO). Our experimental evaluation on multi-turn reasoning and search-based tool-use tasks with GRPO implementations highlights the effectiveness of the MDP framework and the turn-level credit assignment in advancing the multi-turn reasoning capabilities of LLM agents in complex decision-making settings. Our method achieves 100% success in tool execution and 50% accuracy in exact answer matching, significantly outperforming baselines, which fail to invoke tools and achieve only 20-30% exact match accuracy.

Multi-modal Time Series Analysis: A Tutorial and Survey

Multi-modal time series analysis has recently emerged as a prominent research area in data mining, driven by the increasing availability of diverse data modalities, such as text, images, and structured tabular data from real-world sources. However, effective analysis of multi-modal time series is hindered by data heterogeneity, modality gap, misalignment, and inherent noise. Recent advancements in multi-modal time series methods have exploited the multi-modal context via cross-modal interactions based on deep learning methods, significantly enhancing various downstream tasks. In this tutorial and survey, we present a systematic and up-to-date overview of multi-modal time series datasets and methods. We first state the existing challenges of multi-modal time series analysis and our motivations, with a brief introduction of preliminaries. Then, we summarize the general pipeline and categorize existing methods through a unified cross-modal interaction framework encompassing fusion, alignment, and transference at different levels (\textit{i.e.}, input, intermediate, output), where key concepts and ideas are highlighted. We also discuss the real-world applications of multi-modal analysis for both standard and spatial time series, tailored to general and specific domains. Finally, we discuss future research directions to help practitioners explore and exploit multi-modal time series. The up-to-date resources are provided in the GitHub repository: https://github.com/UConn-DSIS/Multi-modal-Time-Series-Analysis

Privacy Amplification by Structured Subsampling for Deep Differentially Private Time Series Forecasting

Many forms of sensitive data, such as web traffic, mobility data, or hospital occupancy, are inherently sequential. The standard method for training machine learning models while ensuring privacy for units of sensitive information, such as individual hospital visits, is differentially private stochastic gradient descent (DP-SGD). However, we observe in this work that the formal guarantees of DP-SGD are incompatible with timeseries-specific tasks like forecasting, since they rely on the privacy amplification attained by training on small, unstructured batches sampled from an unstructured dataset. In contrast, batches for forecasting are generated by (1) sampling sequentially structured time series from a dataset, (2) sampling contiguous subsequences from these series, and (3) partitioning them into context and ground-truth forecast windows. We theoretically analyze the privacy amplification attained by this structured subsampling to enable the training of forecasting models with sound and tight event- and user-level privacy guarantees. Towards more private models, we additionally prove how data augmentation amplifies privacy in self-supervised training of sequence models. Our empirical evaluation demonstrates that amplification by structured subsampling enables the training of forecasting models with strong formal privacy guarantees.

Variational Schrödinger Momentum Diffusion

The momentum Schr\"odinger Bridge (mSB) has emerged as a leading method for accelerating generative diffusion processes and reducing transport costs. However, the lack of simulation-free properties inevitably results in high training costs and affects scalability. To obtain a trade-off between transport properties and scalability, we introduce variational Schr\"odinger momentum diffusion (VSMD), which employs linearized forward score functions (variational scores) to eliminate the dependence on simulated forward trajectories. Our approach leverages a multivariate diffusion process with adaptively transport-optimized variational scores. Additionally, we apply a critical-damping transform to stabilize training by removing the need for score estimations for both velocity and samples. Theoretically, we prove the convergence of samples generated with optimal variational scores and momentum diffusion. Empirical results demonstrate that VSMD efficiently generates anisotropic shapes while maintaining transport efficacy, outperforming overdamped alternatives, and avoiding complex denoising processes. Our approach also scales effectively to real-world data, achieving competitive results in time series and image generation.

Reweighting Improves Conditional Risk Bounds

In this work, we study the weighted empirical risk minimization (weighted ERM) schema, in which an additional data-dependent weight function is incorporated when the empirical risk function is being minimized. We show that under a general ``balanceable" Bernstein condition, one can design a weighted ERM estimator to achieve superior performance in certain sub-regions over the one obtained from standard ERM, and the superiority manifests itself through a data-dependent constant term in the error bound. These sub-regions correspond to large-margin ones in classification settings and low-variance ones in heteroscedastic regression settings, respectively. Our findings are supported by evidence from synthetic data experiments.

Prediction-Enhanced Monte Carlo: A Machine Learning View on Control Variate

Despite being an essential tool across engineering and finance, Monte Carlo simulation can be computationally intensive, especially in large-scale, path-dependent problems that hinder straightforward parallelization. A natural alternative is to replace simulation with machine learning or surrogate prediction, though this introduces challenges in understanding the resulting errors.We introduce a Prediction-Enhanced Monte Carlo (PEMC) framework where we leverage machine learning prediction as control variates, thus maintaining unbiased evaluations instead of the direct use of ML predictors. Traditional control variate methods require knowledge of means and focus on per-sample variance reduction. In contrast, PEMC aims at overall cost-aware variance reduction, eliminating the need for mean knowledge. PEMC leverages pre-trained neural architectures to construct effective control variates and replaces computationally expensive sample-path generation with efficient neural network evaluations. This allows PEMC to address scenarios where no good control variates are known. We showcase the efficacy of PEMC through two production-grade exotic option-pricing problems: swaption pricing in HJM model and the variance swap pricing in a stochastic local volatility model.

Variational Schrödinger Diffusion Models

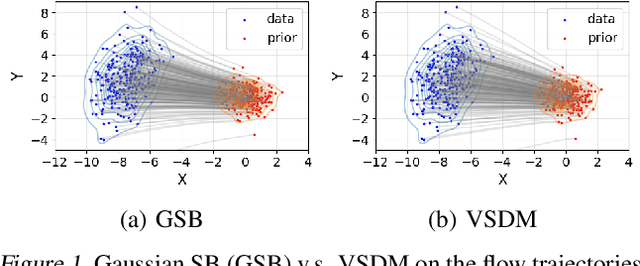
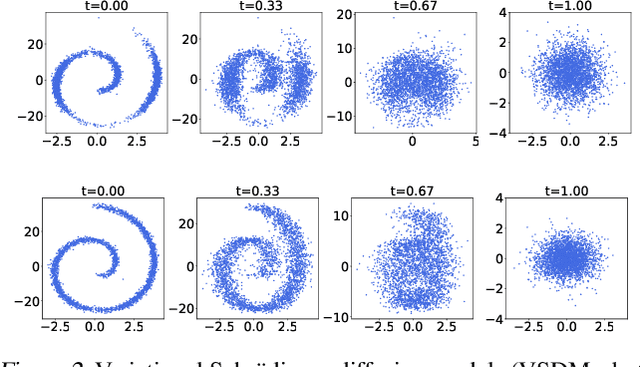
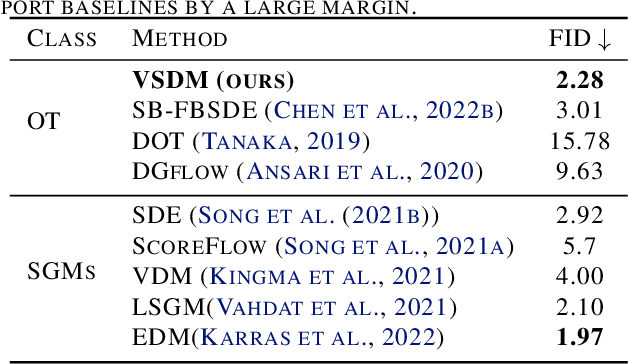
Schr\"odinger bridge (SB) has emerged as the go-to method for optimizing transportation plans in diffusion models. However, SB requires estimating the intractable forward score functions, inevitably resulting in the costly implicit training loss based on simulated trajectories. To improve the scalability while preserving efficient transportation plans, we leverage variational inference to linearize the forward score functions (variational scores) of SB and restore simulation-free properties in training backward scores. We propose the variational Schr\"odinger diffusion model (VSDM), where the forward process is a multivariate diffusion and the variational scores are adaptively optimized for efficient transport. Theoretically, we use stochastic approximation to prove the convergence of the variational scores and show the convergence of the adaptively generated samples based on the optimal variational scores. Empirically, we test the algorithm in simulated examples and observe that VSDM is efficient in generations of anisotropic shapes and yields straighter sample trajectories compared to the single-variate diffusion. We also verify the scalability of the algorithm in real-world data and achieve competitive unconditional generation performance in CIFAR10 and conditional generation in time series modeling. Notably, VSDM no longer depends on warm-up initializations and has become tuning-friendly in training large-scale experiments.