Prediction-Enhanced Monte Carlo: A Machine Learning View on Control Variate

Despite being an essential tool across engineering and finance, Monte Carlo simulation can be computationally intensive, especially in large-scale, path-dependent problems that hinder straightforward parallelization. A natural alternative is to replace simulation with machine learning or surrogate prediction, though this introduces challenges in understanding the resulting errors.We introduce a Prediction-Enhanced Monte Carlo (PEMC) framework where we leverage machine learning prediction as control variates, thus maintaining unbiased evaluations instead of the direct use of ML predictors. Traditional control variate methods require knowledge of means and focus on per-sample variance reduction. In contrast, PEMC aims at overall cost-aware variance reduction, eliminating the need for mean knowledge. PEMC leverages pre-trained neural architectures to construct effective control variates and replaces computationally expensive sample-path generation with efficient neural network evaluations. This allows PEMC to address scenarios where no good control variates are known. We showcase the efficacy of PEMC through two production-grade exotic option-pricing problems: swaption pricing in HJM model and the variance swap pricing in a stochastic local volatility model.

Causal Inference (C-inf) -- asymmetric scenario of typical phase transitions

In this paper, we revisit and further explore a mathematically rigorous connection between Causal inference (C-inf) and the Low-rank recovery (LRR) established in [10]. Leveraging the Random duality - Free probability theory (RDT-FPT) connection, we obtain the exact explicit typical C-inf asymmetric phase transitions (PT). We uncover a doubling low-rankness phenomenon, which means that exactly two times larger low rankness is allowed in asymmetric scenarios compared to the symmetric worst case ones considered in [10]. Consequently, the final PT mathematical expressions are as elegant as those obtained in [10], and highlight direct relations between the targeted C-inf matrix low rankness and the time of treatment. Our results have strong implications for applications, where C-inf matrices are not necessarily symmetric.

Causal Inference (C-inf) -- closed form worst case typical phase transitions

In this paper we establish a mathematically rigorous connection between Causal inference (C-inf) and the low-rank recovery (LRR). Using Random Duality Theory (RDT) concepts developed in [46,48,50] and novel mathematical strategies related to free probability theory, we obtain the exact explicit typical (and achievable) worst case phase transitions (PT). These PT precisely separate scenarios where causal inference via LRR is possible from those where it is not. We supplement our mathematical analysis with numerical experiments that confirm the theoretical predictions of PT phenomena, and further show that the two closely match for fairly small sample sizes. We obtain simple closed form representations for the resulting PTs, which highlight direct relations between the low rankness of the target C-inf matrix and the time of the treatment. Hence, our results can be used to determine the range of C-inf's typical applicability.

Robo-advising: Learning Investors' Risk Preferences via Portfolio Choices

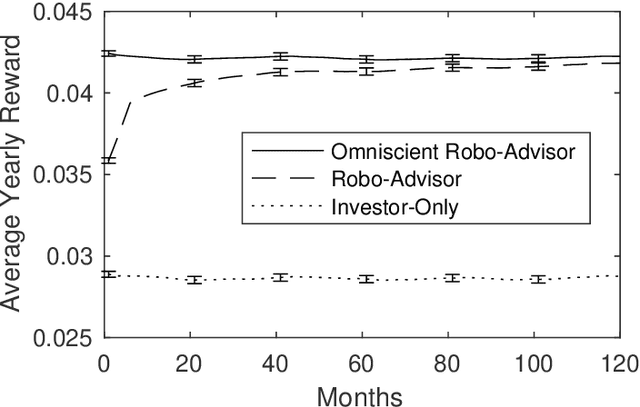
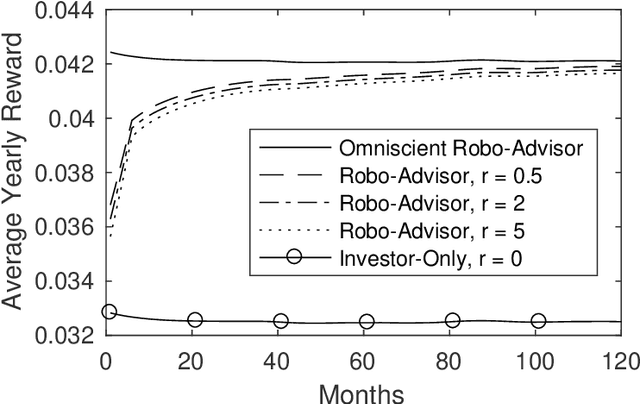
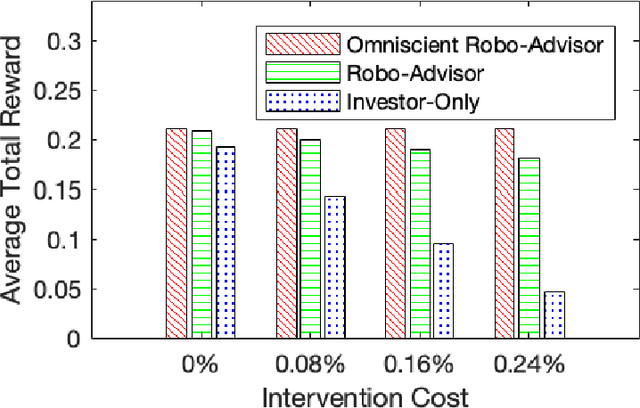
We introduce a reinforcement learning framework for retail robo-advising. The robo-advisor does not know the investor's risk preference, but learns it over time by observing her portfolio choices in different market environments. We develop an exploration-exploitation algorithm which trades off costly solicitations of portfolio choices by the investor with autonomous trading decisions based on stale estimates of investor's risk aversion. We show that the algorithm's value function converges to the optimal value function of an omniscient robo-advisor over a number of periods that is polynomial in the state and action space. By correcting for the investor's mistakes, the robo-advisor may outperform a stand-alone investor, regardless of the investor's opportunity cost for making portfolio decisions.

Risk-Sensitive Cooperative Games for Human-Machine Systems

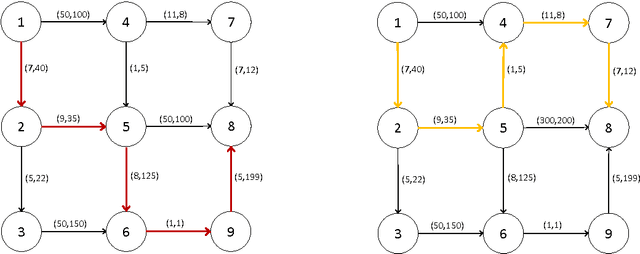
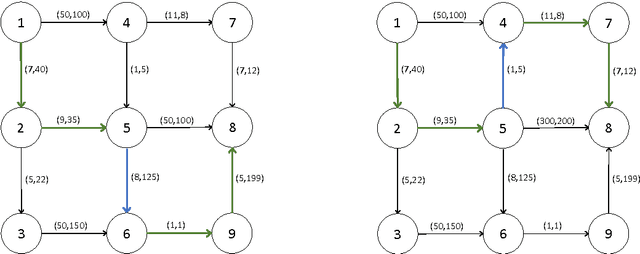
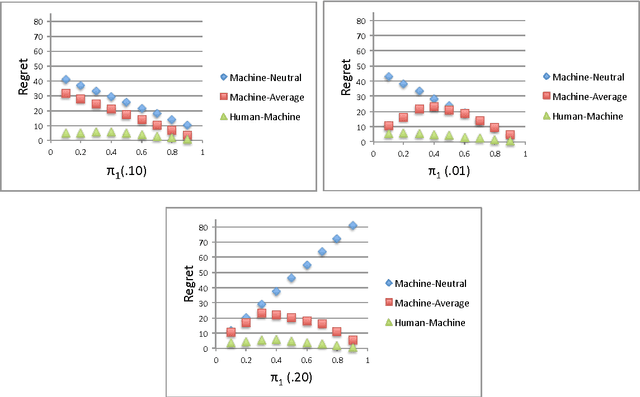
Autonomous systems can substantially enhance a human's efficiency and effectiveness in complex environments. Machines, however, are often unable to observe the preferences of the humans that they serve. Despite the fact that the human's and machine's objectives are aligned, asymmetric information, along with heterogeneous sensitivities to risk by the human and machine, make their joint optimization process a game with strategic interactions. We propose a framework based on risk-sensitive dynamic games; the human seeks to optimize her risk-sensitive criterion according to her true preferences, while the machine seeks to adaptively learn the human's preferences and at the same time provide a good service to the human. We develop a class of performance measures for the proposed framework based on the concept of regret. We then evaluate their dependence on the risk-sensitivity and the degree of uncertainty. We present applications of our framework to self-driving taxis, and robo-financial advising.