Reweighting Improves Conditional Risk Bounds

In this work, we study the weighted empirical risk minimization (weighted ERM) schema, in which an additional data-dependent weight function is incorporated when the empirical risk function is being minimized. We show that under a general ``balanceable" Bernstein condition, one can design a weighted ERM estimator to achieve superior performance in certain sub-regions over the one obtained from standard ERM, and the superiority manifests itself through a data-dependent constant term in the error bound. These sub-regions correspond to large-margin ones in classification settings and low-variance ones in heteroscedastic regression settings, respectively. Our findings are supported by evidence from synthetic data experiments.

Prediction-Enhanced Monte Carlo: A Machine Learning View on Control Variate

Despite being an essential tool across engineering and finance, Monte Carlo simulation can be computationally intensive, especially in large-scale, path-dependent problems that hinder straightforward parallelization. A natural alternative is to replace simulation with machine learning or surrogate prediction, though this introduces challenges in understanding the resulting errors.We introduce a Prediction-Enhanced Monte Carlo (PEMC) framework where we leverage machine learning prediction as control variates, thus maintaining unbiased evaluations instead of the direct use of ML predictors. Traditional control variate methods require knowledge of means and focus on per-sample variance reduction. In contrast, PEMC aims at overall cost-aware variance reduction, eliminating the need for mean knowledge. PEMC leverages pre-trained neural architectures to construct effective control variates and replaces computationally expensive sample-path generation with efficient neural network evaluations. This allows PEMC to address scenarios where no good control variates are known. We showcase the efficacy of PEMC through two production-grade exotic option-pricing problems: swaption pricing in HJM model and the variance swap pricing in a stochastic local volatility model.

Short-term Temporal Dependency Detection under Heterogeneous Event Dynamic with Hawkes Processes

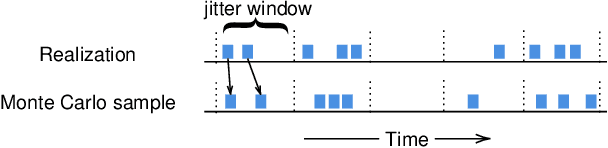
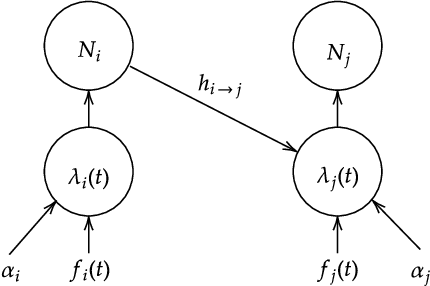
Many event sequence data exhibit mutually exciting or inhibiting patterns. Reliable detection of such temporal dependency is crucial for scientific investigation. The de facto model is the Multivariate Hawkes Process (MHP), whose impact function naturally encodes a causal structure in Granger causality. However, the vast majority of existing methods use direct or nonlinear transform of standard MHP intensity with constant baseline, inconsistent with real-world data. Under irregular and unknown heterogeneous intensity, capturing temporal dependency is hard as one struggles to distinguish the effect of mutual interaction from that of intensity fluctuation. In this paper, we address the short-term temporal dependency detection issue. We show the maximum likelihood estimation (MLE) for cross-impact from MHP has an error that can not be eliminated but may be reduced by order of magnitude, using heterogeneous intensity not of the target HP but of the interacting HP. Then we proposed a robust and computationally-efficient method modified from MLE that does not rely on the prior estimation of the heterogeneous intensity and is thus applicable in a data-limited regime (e.g., few-shot, no repeated observations). Extensive experiments on various datasets show that our method outperforms existing ones by notable margins, with highlighted novel applications in neuroscience.

Provably Convergent Schrödinger Bridge with Applications to Probabilistic Time Series Imputation

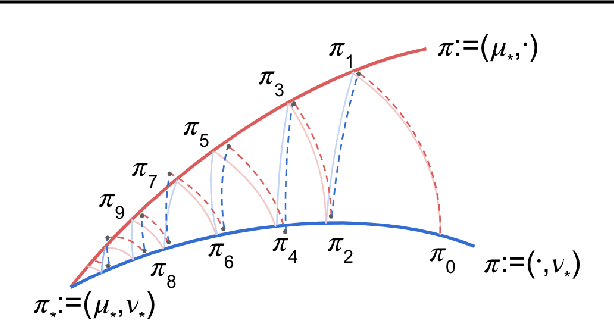
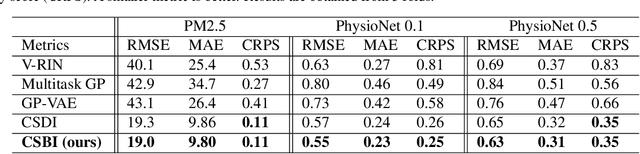
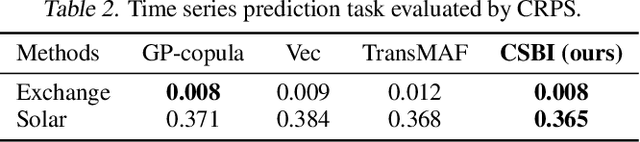
The Schr\"odinger bridge problem (SBP) is gaining increasing attention in generative modeling and showing promising potential even in comparison with the score-based generative models (SGMs). SBP can be interpreted as an entropy-regularized optimal transport problem, which conducts projections onto every other marginal alternatingly. However, in practice, only approximated projections are accessible and their convergence is not well understood. To fill this gap, we present a first convergence analysis of the Schr\"odinger bridge algorithm based on approximated projections. As for its practical applications, we apply SBP to probabilistic time series imputation by generating missing values conditioned on observed data. We show that optimizing the transport cost improves the performance and the proposed algorithm achieves the state-of-the-art result in healthcare and environmental data while exhibiting the advantage of exploring both temporal and feature patterns in probabilistic time series imputation.

Accelerated Policy Evaluation: Learning Adversarial Environments with Adaptive Importance Sampling

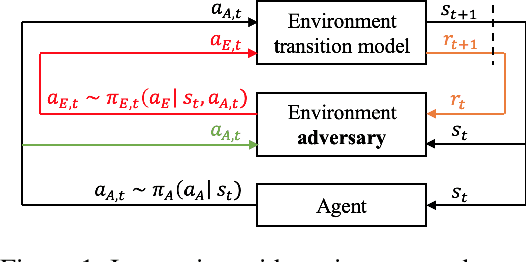
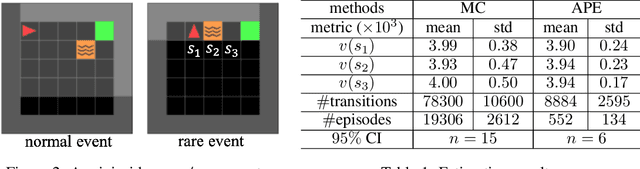
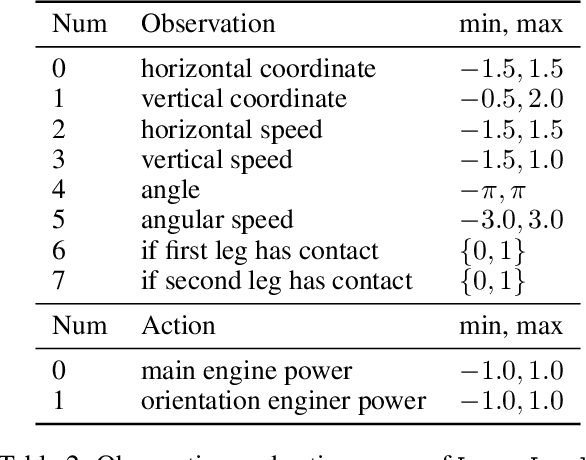
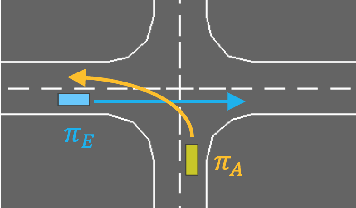
The evaluation of rare but high-stakes events remains one of the main difficulties in obtaining reliable policies from intelligent agents, especially in large or continuous state/action spaces where limited scalability enforces the use of a prohibitively large number of testing iterations. On the other hand, a biased or inaccurate policy evaluation in a safety-critical system could potentially cause unexpected catastrophic failures during deployment. In this paper, we propose the Accelerated Policy Evaluation (APE) method, which simultaneously uncovers rare events and estimates the rare event probability in Markov decision processes. The APE method treats the environment nature as an adversarial agent and learns towards, through adaptive importance sampling, the zero-variance sampling distribution for the policy evaluation. Moreover, APE is scalable to large discrete or continuous spaces by incorporating function approximators. We investigate the convergence properties of proposed algorithms under suitable regularity conditions. Our empirical studies show that APE estimates rare event probability with a smaller variance while only using orders of magnitude fewer samples compared to baseline methods in both multi-agent and single-agent environments.

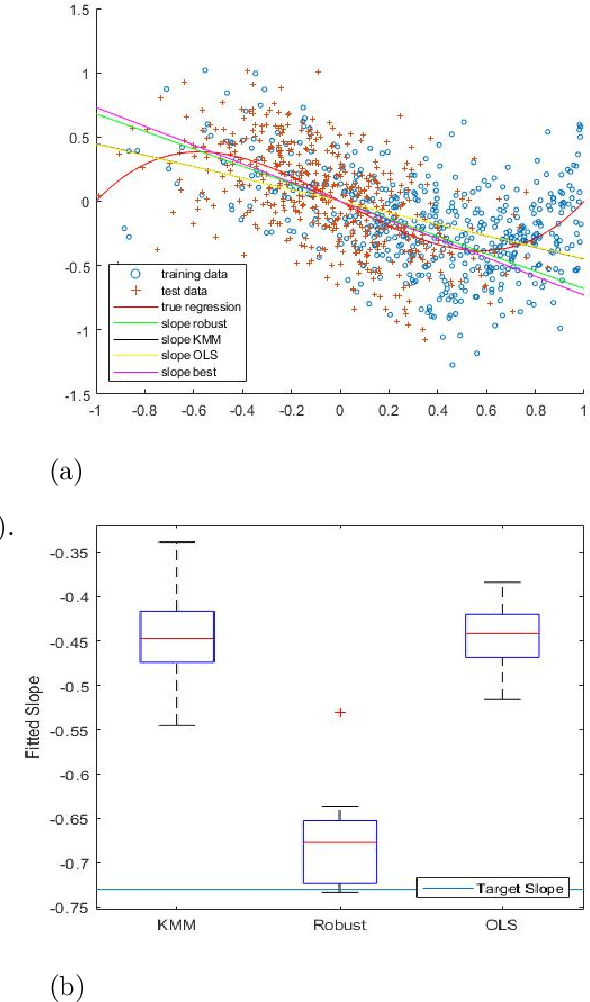
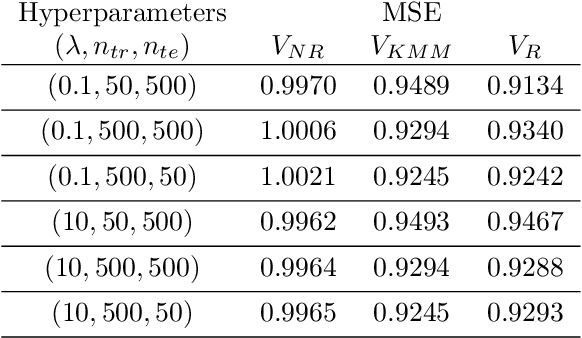
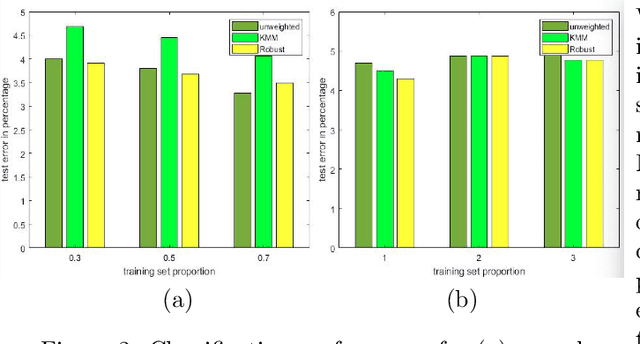
Robust Importance Weighting for Covariate Shift

In many learning problems, the training and testing data follow different distributions and a particularly common situation is the \textit{covariate shift}. To correct for sampling biases, most approaches, including the popular kernel mean matching (KMM), focus on estimating the importance weights between the two distributions. Reweighting-based methods, however, are exposed to high variance when the distributional discrepancy is large and the weights are poorly estimated. On the other hand, the alternate approach of using nonparametric regression (NR) incurs high bias when the training size is limited. In this paper, we propose and analyze a new estimator that systematically integrates the residuals of NR with KMM reweighting, based on a control-variate perspective. The proposed estimator can be shown to either strictly outperform or match the best-known existing rates for both KMM and NR, and thus is a robust combination of both estimators. The experiments shows the estimator works well in practice.