Recurrent Interpolants for Probabilistic Time Series Prediction

Sequential models such as recurrent neural networks or transformer-based models became \textit{de facto} tools for multivariate time series forecasting in a probabilistic fashion, with applications to a wide range of datasets, such as finance, biology, medicine, etc. Despite their adeptness in capturing dependencies, assessing prediction uncertainty, and efficiency in training, challenges emerge in modeling high-dimensional complex distributions and cross-feature dependencies. To tackle these issues, recent works delve into generative modeling by employing diffusion or flow-based models. Notably, the integration of stochastic differential equations or probability flow successfully extends these methods to probabilistic time series imputation and forecasting. However, scalability issues necessitate a computational-friendly framework for large-scale generative model-based predictions. This work proposes a novel approach by blending the computational efficiency of recurrent neural networks with the high-quality probabilistic modeling of the diffusion model, which addresses challenges and advances generative models' application in time series forecasting. Our method relies on the foundation of stochastic interpolants and the extension to a broader conditional generation framework with additional control features, offering insights for future developments in this dynamic field.

Variational Schrödinger Diffusion Models

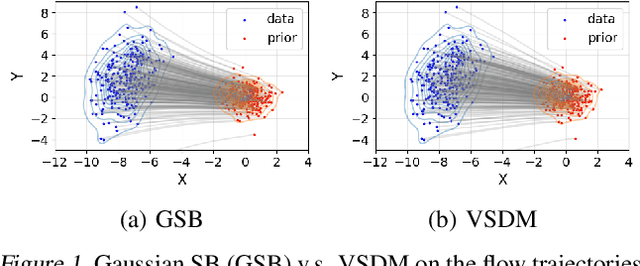
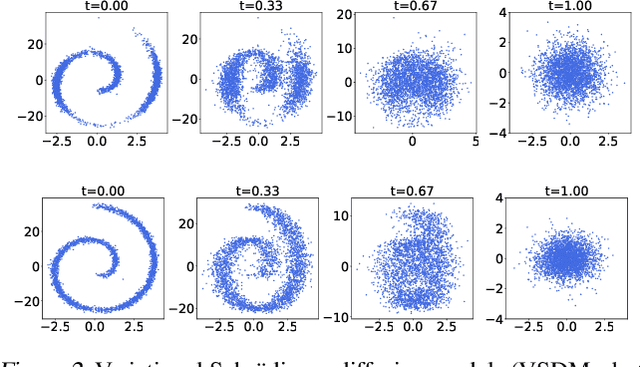
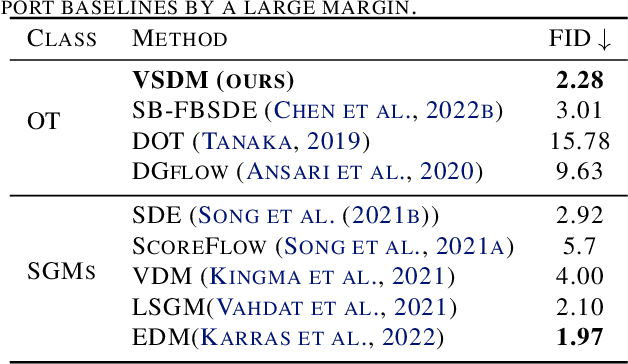
Schr\"odinger bridge (SB) has emerged as the go-to method for optimizing transportation plans in diffusion models. However, SB requires estimating the intractable forward score functions, inevitably resulting in the costly implicit training loss based on simulated trajectories. To improve the scalability while preserving efficient transportation plans, we leverage variational inference to linearize the forward score functions (variational scores) of SB and restore simulation-free properties in training backward scores. We propose the variational Schr\"odinger diffusion model (VSDM), where the forward process is a multivariate diffusion and the variational scores are adaptively optimized for efficient transport. Theoretically, we use stochastic approximation to prove the convergence of the variational scores and show the convergence of the adaptively generated samples based on the optimal variational scores. Empirically, we test the algorithm in simulated examples and observe that VSDM is efficient in generations of anisotropic shapes and yields straighter sample trajectories compared to the single-variate diffusion. We also verify the scalability of the algorithm in real-world data and achieve competitive unconditional generation performance in CIFAR10 and conditional generation in time series modeling. Notably, VSDM no longer depends on warm-up initializations and has become tuning-friendly in training large-scale experiments.

Add and Thin: Diffusion for Temporal Point Processes

Autoregressive neural networks within the temporal point process (TPP) framework have become the standard for modeling continuous-time event data. Even though these models can expressively capture event sequences in a one-step-ahead fashion, they are inherently limited for long-term forecasting applications due to the accumulation of errors caused by their sequential nature. To overcome these limitations, we derive ADD-THIN, a principled probabilistic denoising diffusion model for TPPs that operates on entire event sequences. Unlike existing diffusion approaches, ADD-THIN naturally handles data with discrete and continuous components. In experiments on synthetic and real-world datasets, our model matches the state-of-the-art TPP models in density estimation and strongly outperforms them in forecasting.

Lag-Llama: Towards Foundation Models for Time Series Forecasting

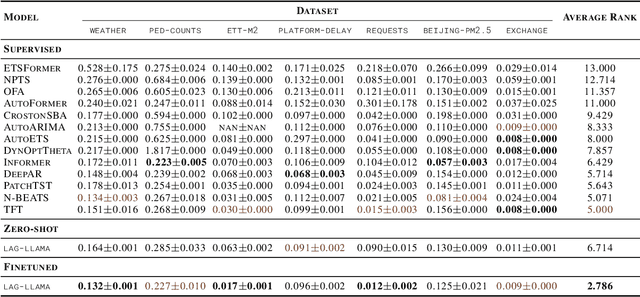
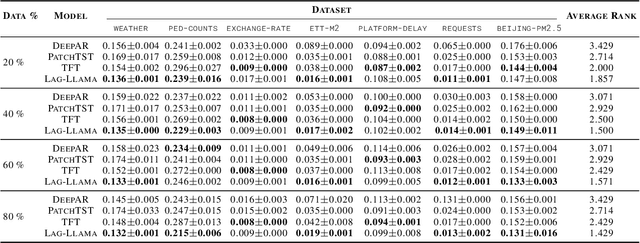
Aiming to build foundation models for time-series forecasting and study their scaling behavior, we present here our work-in-progress on Lag-Llama, a general-purpose univariate probabilistic time-series forecasting model trained on a large collection of time-series data. The model shows good zero-shot prediction capabilities on unseen "out-of-distribution" time-series datasets, outperforming supervised baselines. We use smoothly broken power-laws to fit and predict model scaling behavior. The open source code is made available at https://github.com/kashif/pytorch-transformer-ts.

Modeling Temporal Data as Continuous Functions with Process Diffusion

Temporal data like time series are often observed at irregular intervals which is a challenging setting for existing machine learning methods. To tackle this problem, we view such data as samples from some underlying continuous function. We then define a diffusion-based generative model that adds noise from a predefined stochastic process while preserving the continuity of the resulting underlying function. A neural network is trained to reverse this process which allows us to sample new realizations from the learned distribution. We define suitable stochastic processes as noise sources and introduce novel denoising and score-matching models on processes. Further, we show how to apply this approach to the multivariate probabilistic forecasting and imputation tasks. Through our extensive experiments, we demonstrate that our method outperforms previous models on synthetic and real-world datasets.

Irregularly-Sampled Time Series Modeling with Spline Networks

Observations made in continuous time are often irregular and contain the missing values across different channels. One approach to handle the missing data is imputing it using splines, by fitting the piecewise polynomials to the observed values. We propose using the splines as an input to a neural network, in particular, applying the transformations on the interpolating function directly, instead of sampling the points on a grid. To do that, we design the layers that can operate on splines and which are analogous to their discrete counterparts. This allows us to represent the irregular sequence compactly and use this representation in the downstream tasks such as classification and forecasting. Our model offers competitive performance compared to the existing methods both in terms of the accuracy and computation efficiency.

Neural Flows: Efficient Alternative to Neural ODEs

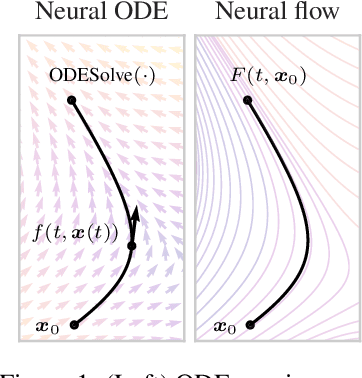
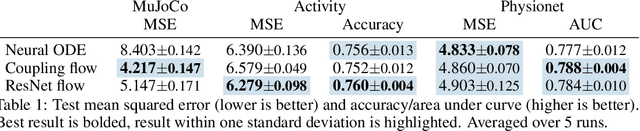
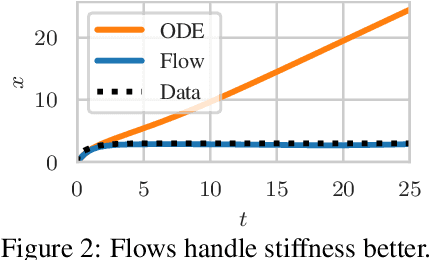
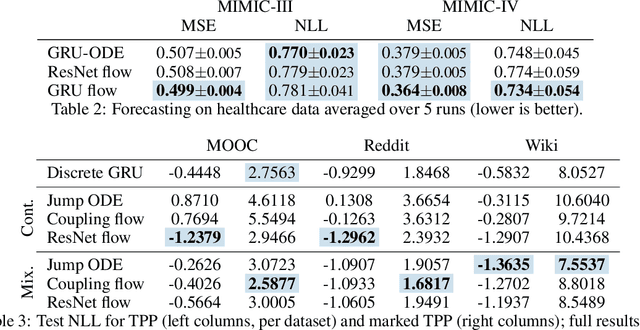
Neural ordinary differential equations describe how values change in time. This is the reason why they gained importance in modeling sequential data, especially when the observations are made at irregular intervals. In this paper we propose an alternative by directly modeling the solution curves - the flow of an ODE - with a neural network. This immediately eliminates the need for expensive numerical solvers while still maintaining the modeling capability of neural ODEs. We propose several flow architectures suitable for different applications by establishing precise conditions on when a function defines a valid flow. Apart from computational efficiency, we also provide empirical evidence of favorable generalization performance via applications in time series modeling, forecasting, and density estimation.

Equivariant Normalizing Flows for Point Processes and Sets

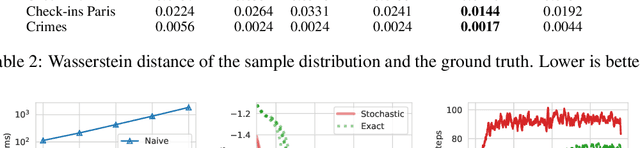
A point process describes how random sets of exchangeable points are generated. The points usually influence the positions of each other via attractive and repulsive forces. To model this behavior, it is enough to transform the samples from the uniform process with a sufficiently complex equivariant function. However, learning the parameters of the resulting process is challenging since the likelihood is hard to estimate and often intractable. This leads us to our proposed model - CONFET. Based on continuous normalizing flows, it allows arbitrary interactions between points while having tractable likelihood. Experiments on various real and synthetic datasets show the improved performance of our new scalable approach.

Deep Representation Learning and Clustering of Traffic Scenarios

Determining the traffic scenario space is a major challenge for the homologation and coverage assessment of automated driving functions. In contrast to current approaches that are mainly scenario-based and rely on expert knowledge, we introduce two data driven autoencoding models that learn a latent representation of traffic scenes. First is a CNN based spatio-temporal model that autoencodes a grid of traffic participants' positions. Secondly, we develop a pure temporal RNN based model that auto-encodes a sequence of sets. To handle the unordered set data, we had to incorporate the permutation invariance property. Finally, we show how the latent scenario embeddings can be used for clustering traffic scenarios and similarity retrieval.

Fast and Flexible Temporal Point Processes with Triangular Maps

Temporal point process (TPP) models combined with recurrent neural networks provide a powerful framework for modeling continuous-time event data. While such models are flexible, they are inherently sequential and therefore cannot benefit from the parallelism of modern hardware. By exploiting the recent developments in the field of normalizing flows, we design TriTPP -- a new class of non-recurrent TPP models, where both sampling and likelihood computation can be done in parallel. TriTPP matches the flexibility of RNN-based methods but permits orders of magnitude faster sampling. This enables us to use the new model for variational inference in continuous-time discrete-state systems. We demonstrate the advantages of the proposed framework on synthetic and real-world datasets.