Unlocking Point Processes through Point Set Diffusion

Point processes model the distribution of random point sets in mathematical spaces, such as spatial and temporal domains, with applications in fields like seismology, neuroscience, and economics. Existing statistical and machine learning models for point processes are predominantly constrained by their reliance on the characteristic intensity function, introducing an inherent trade-off between efficiency and flexibility. In this paper, we introduce Point Set Diffusion, a diffusion-based latent variable model that can represent arbitrary point processes on general metric spaces without relying on the intensity function. By directly learning to stochastically interpolate between noise and data point sets, our approach enables efficient, parallel sampling and flexible generation for complex conditional tasks defined on the metric space. Experiments on synthetic and real-world datasets demonstrate that Point Set Diffusion achieves state-of-the-art performance in unconditional and conditional generation of spatial and spatiotemporal point processes while providing up to orders of magnitude faster sampling than autoregressive baselines.

Flow Matching with Gaussian Process Priors for Probabilistic Time Series Forecasting

Recent advancements in generative modeling, particularly diffusion models, have opened new directions for time series modeling, achieving state-of-the-art performance in forecasting and synthesis. However, the reliance of diffusion-based models on a simple, fixed prior complicates the generative process since the data and prior distributions differ significantly. We introduce TSFlow, a conditional flow matching (CFM) model for time series that simplifies the generative problem by combining Gaussian processes, optimal transport paths, and data-dependent prior distributions. By incorporating (conditional) Gaussian processes, TSFlow aligns the prior distribution more closely with the temporal structure of the data, enhancing both unconditional and conditional generation. Furthermore, we propose conditional prior sampling to enable probabilistic forecasting with an unconditionally trained model. In our experimental evaluation on eight real-world datasets, we demonstrate the generative capabilities of TSFlow, producing high-quality unconditional samples. Finally, we show that both conditionally and unconditionally trained models achieve competitive results in forecasting benchmarks, surpassing other methods on 6 out of 8 datasets.

Add and Thin: Diffusion for Temporal Point Processes

Autoregressive neural networks within the temporal point process (TPP) framework have become the standard for modeling continuous-time event data. Even though these models can expressively capture event sequences in a one-step-ahead fashion, they are inherently limited for long-term forecasting applications due to the accumulation of errors caused by their sequential nature. To overcome these limitations, we derive ADD-THIN, a principled probabilistic denoising diffusion model for TPPs that operates on entire event sequences. Unlike existing diffusion approaches, ADD-THIN naturally handles data with discrete and continuous components. In experiments on synthetic and real-world datasets, our model matches the state-of-the-art TPP models in density estimation and strongly outperforms them in forecasting.

Generative Diffusion for 3D Turbulent Flows

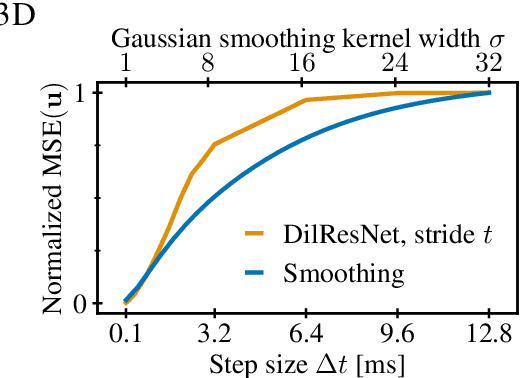
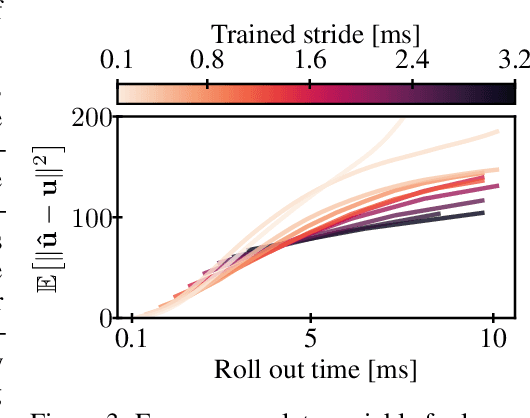
Turbulent flows are well known to be chaotic and hard to predict; however, their dynamics differ between two and three dimensions. While 2D turbulence tends to form large, coherent structures, in three dimensions vortices cascade to smaller and smaller scales. This cascade creates many fast-changing, small-scale structures and amplifies the unpredictability, making regression-based methods infeasible. We propose the first generative model for forced turbulence in arbitrary 3D geometries and introduce a sample quality metric for turbulent flows based on the Wasserstein distance of the generated velocity-vorticity distribution. In several experiments, we show that our generative diffusion model circumvents the unpredictability of turbulent flows and produces high-quality samples based solely on geometric information. Furthermore, we demonstrate that our model beats an industrial-grade numerical solver in the time to generate a turbulent flow field from scratch by an order of magnitude.

Landmark-free Statistical Shape Modeling via Neural Flow Deformations

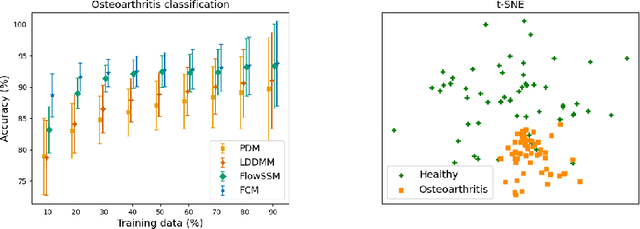
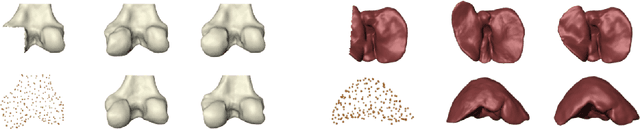
Statistical shape modeling aims at capturing shape variations of an anatomical structure that occur within a given population. Shape models are employed in many tasks, such as shape reconstruction and image segmentation, but also shape generation and classification. Existing shape priors either require dense correspondence between training examples or lack robustness and topological guarantees. We present FlowSSM, a novel shape modeling approach that learns shape variability without requiring dense correspondence between training instances. It relies on a hierarchy of continuous deformation flows, which are parametrized by a neural network. Our model outperforms state-of-the-art methods in providing an expressive and robust shape prior for distal femur and liver. We show that the emerging latent representation is discriminative by separating healthy from pathological shapes. Ultimately, we demonstrate its effectiveness on two shape reconstruction tasks from partial data. Our source code is publicly available (https://github.com/davecasp/flowssm).