Flow Matching with Gaussian Process Priors for Probabilistic Time Series Forecasting

Recent advancements in generative modeling, particularly diffusion models, have opened new directions for time series modeling, achieving state-of-the-art performance in forecasting and synthesis. However, the reliance of diffusion-based models on a simple, fixed prior complicates the generative process since the data and prior distributions differ significantly. We introduce TSFlow, a conditional flow matching (CFM) model for time series that simplifies the generative problem by combining Gaussian processes, optimal transport paths, and data-dependent prior distributions. By incorporating (conditional) Gaussian processes, TSFlow aligns the prior distribution more closely with the temporal structure of the data, enhancing both unconditional and conditional generation. Furthermore, we propose conditional prior sampling to enable probabilistic forecasting with an unconditionally trained model. In our experimental evaluation on eight real-world datasets, we demonstrate the generative capabilities of TSFlow, producing high-quality unconditional samples. Finally, we show that both conditionally and unconditionally trained models achieve competitive results in forecasting benchmarks, surpassing other methods on 6 out of 8 datasets.

Unfolding Time: Generative Modeling for Turbulent Flows in 4D

A recent study in turbulent flow simulation demonstrated the potential of generative diffusion models for fast 3D surrogate modeling. This approach eliminates the need for specifying initial states or performing lengthy simulations, significantly accelerating the process. While adept at sampling individual frames from the learned manifold of turbulent flow states, the previous model lacks the capability to generate sequences, hindering analysis of dynamic phenomena. This work addresses this limitation by introducing a 4D generative diffusion model and a physics-informed guidance technique that enables the generation of realistic sequences of flow states. Our findings indicate that the proposed method can successfully sample entire subsequences from the turbulent manifold, even though generalizing from individual frames to sequences remains a challenging task. This advancement opens doors for the application of generative modeling in analyzing the temporal evolution of turbulent flows, providing valuable insights into their complex dynamics.

Add and Thin: Diffusion for Temporal Point Processes

Autoregressive neural networks within the temporal point process (TPP) framework have become the standard for modeling continuous-time event data. Even though these models can expressively capture event sequences in a one-step-ahead fashion, they are inherently limited for long-term forecasting applications due to the accumulation of errors caused by their sequential nature. To overcome these limitations, we derive ADD-THIN, a principled probabilistic denoising diffusion model for TPPs that operates on entire event sequences. Unlike existing diffusion approaches, ADD-THIN naturally handles data with discrete and continuous components. In experiments on synthetic and real-world datasets, our model matches the state-of-the-art TPP models in density estimation and strongly outperforms them in forecasting.

Assessing Robustness via Score-Based Adversarial Image Generation

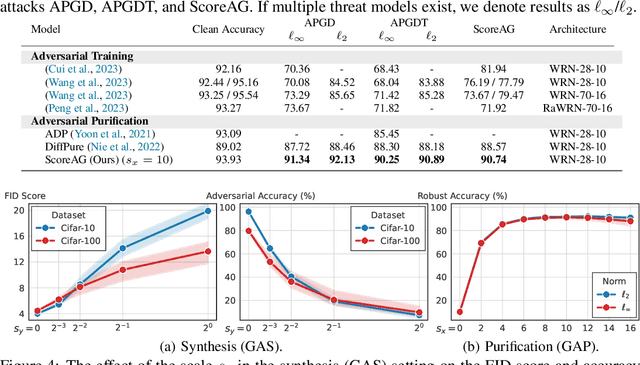
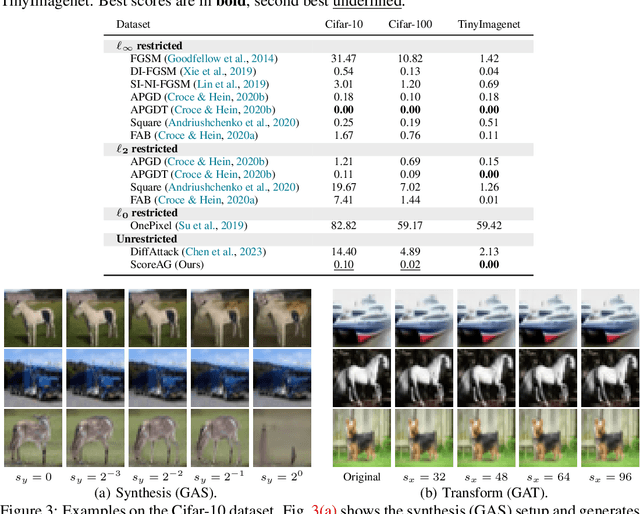
Most adversarial attacks and defenses focus on perturbations within small $\ell_p$-norm constraints. However, $\ell_p$ threat models cannot capture all relevant semantic-preserving perturbations, and hence, the scope of robustness evaluations is limited. In this work, we introduce Score-Based Adversarial Generation (ScoreAG), a novel framework that leverages the advancements in score-based generative models to generate adversarial examples beyond $\ell_p$-norm constraints, so-called unrestricted adversarial examples, overcoming their limitations. Unlike traditional methods, ScoreAG maintains the core semantics of images while generating realistic adversarial examples, either by transforming existing images or synthesizing new ones entirely from scratch. We further exploit the generative capability of ScoreAG to purify images, empirically enhancing the robustness of classifiers. Our extensive empirical evaluation demonstrates that ScoreAG matches the performance of state-of-the-art attacks and defenses across multiple benchmarks. This work highlights the importance of investigating adversarial examples bounded by semantics rather than $\ell_p$-norm constraints. ScoreAG represents an important step towards more encompassing robustness assessments.

Generative Diffusion for 3D Turbulent Flows

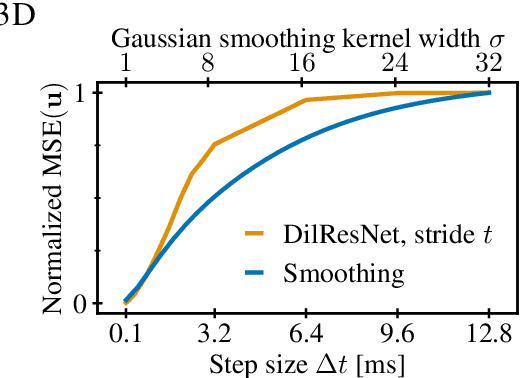
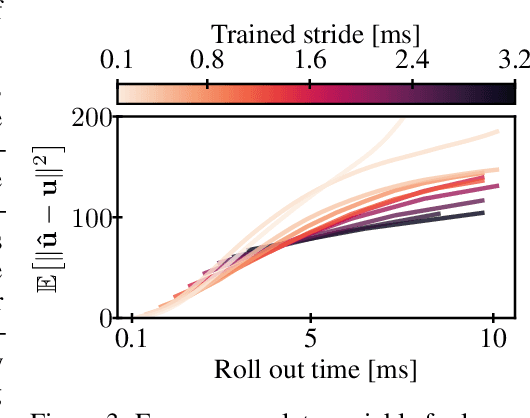
Turbulent flows are well known to be chaotic and hard to predict; however, their dynamics differ between two and three dimensions. While 2D turbulence tends to form large, coherent structures, in three dimensions vortices cascade to smaller and smaller scales. This cascade creates many fast-changing, small-scale structures and amplifies the unpredictability, making regression-based methods infeasible. We propose the first generative model for forced turbulence in arbitrary 3D geometries and introduce a sample quality metric for turbulent flows based on the Wasserstein distance of the generated velocity-vorticity distribution. In several experiments, we show that our generative diffusion model circumvents the unpredictability of turbulent flows and produces high-quality samples based solely on geometric information. Furthermore, we demonstrate that our model beats an industrial-grade numerical solver in the time to generate a turbulent flow field from scratch by an order of magnitude.

Learning the Dynamics of Physical Systems from Sparse Observations with Finite Element Networks

We propose a new method for spatio-temporal forecasting on arbitrarily distributed points. Assuming that the observed system follows an unknown partial differential equation, we derive a continuous-time model for the dynamics of the data via the finite element method. The resulting graph neural network estimates the instantaneous effects of the unknown dynamics on each cell in a meshing of the spatial domain. Our model can incorporate prior knowledge via assumptions on the form of the unknown PDE, which induce a structural bias towards learning specific processes. Through this mechanism, we derive a transport variant of our model from the convection equation and show that it improves the transfer performance to higher-resolution meshes on sea surface temperature and gas flow forecasting against baseline models representing a selection of spatio-temporal forecasting methods. A qualitative analysis shows that our model disentangles the data dynamics into their constituent parts, which makes it uniquely interpretable.

Scalable Optimal Transport in High Dimensions for Graph Distances, Embedding Alignment, and More

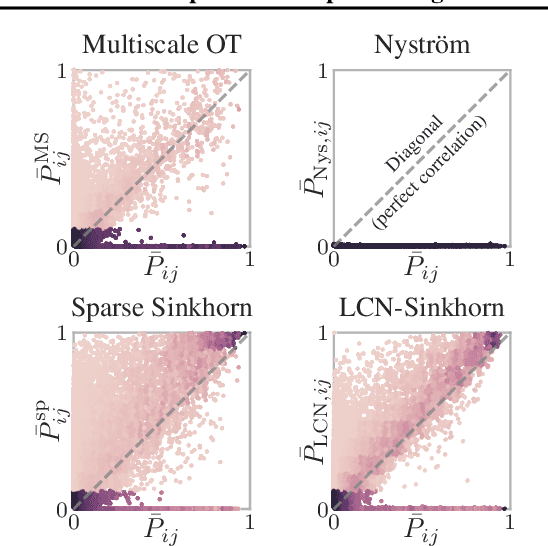
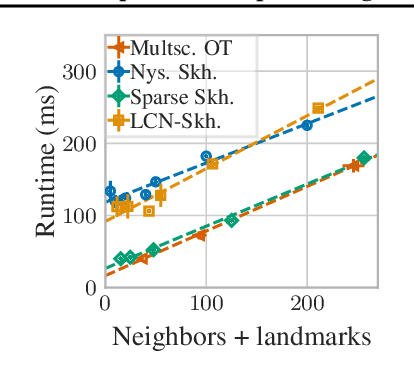
The current best practice for computing optimal transport (OT) is via entropy regularization and Sinkhorn iterations. This algorithm runs in quadratic time as it requires the full pairwise cost matrix, which is prohibitively expensive for large sets of objects. In this work we propose two effective log-linear time approximations of the cost matrix: First, a sparse approximation based on locality-sensitive hashing (LSH) and, second, a Nystr\"om approximation with LSH-based sparse corrections, which we call locally corrected Nystr\"om (LCN). These approximations enable general log-linear time algorithms for entropy-regularized OT that perform well even for the complex, high-dimensional spaces common in deep learning. We analyse these approximations theoretically and evaluate them experimentally both directly and end-to-end as a component for real-world applications. Using our approximations for unsupervised word embedding alignment enables us to speed up a state-of-the-art method by a factor of 3 while also improving the accuracy by 3.1 percentage points without any additional model changes. For graph distance regression we propose the graph transport network (GTN), which combines graph neural networks (GNNs) with enhanced Sinkhorn. GTN outcompetes previous models by 48% and still scales log-linearly in the number of nodes.