Directional Message Passing on Molecular Graphs via Synthetic Coordinates

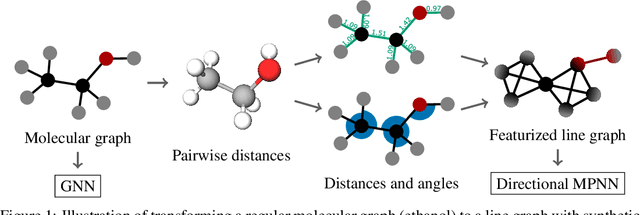
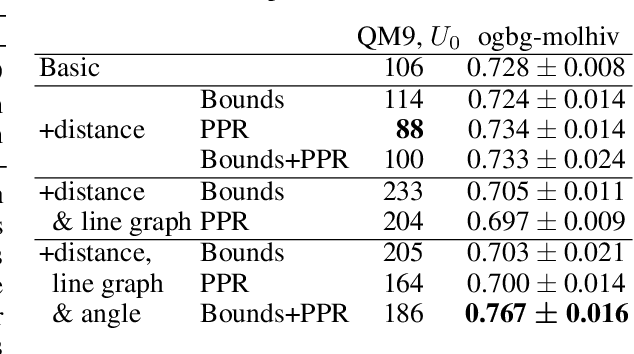
Graph neural networks that leverage coordinates via directional message passing have recently set the state of the art on multiple molecular property prediction tasks. However, they rely on atom position information that is often unavailable, and obtaining it is usually prohibitively expensive or even impossible. In this paper we propose synthetic coordinates that enable the use of advanced GNNs without requiring the true molecular configuration. We propose two distances as synthetic coordinates: Distance bounds that specify the rough range of molecular configurations, and graph-based distances using a symmetric variant of personalized PageRank. To leverage both distance and angular information we propose a method of transforming normal graph neural networks into directional MPNNs. We show that with this transformation we can reduce the error of a normal graph neural network by 55% on the ZINC benchmark. We furthermore set the state of the art on ZINC and coordinate-free QM9 by incorporating synthetic coordinates in the SMP and DimeNet++ models. Our implementation is available online.

Scalable Optimal Transport in High Dimensions for Graph Distances, Embedding Alignment, and More

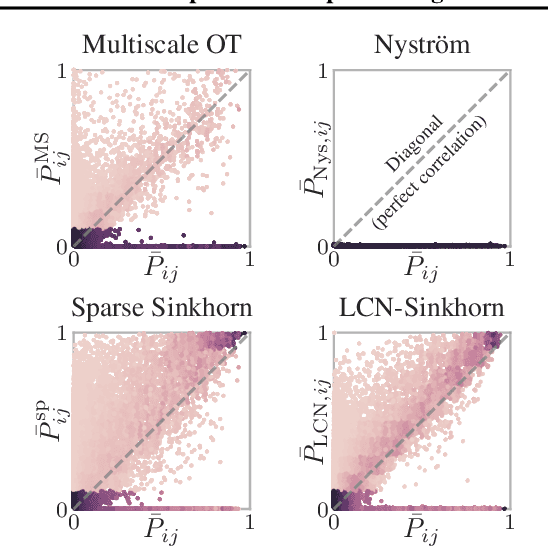
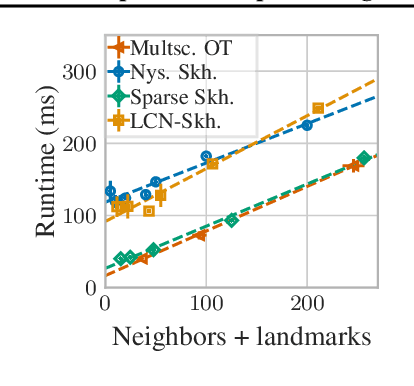
The current best practice for computing optimal transport (OT) is via entropy regularization and Sinkhorn iterations. This algorithm runs in quadratic time as it requires the full pairwise cost matrix, which is prohibitively expensive for large sets of objects. In this work we propose two effective log-linear time approximations of the cost matrix: First, a sparse approximation based on locality-sensitive hashing (LSH) and, second, a Nystr\"om approximation with LSH-based sparse corrections, which we call locally corrected Nystr\"om (LCN). These approximations enable general log-linear time algorithms for entropy-regularized OT that perform well even for the complex, high-dimensional spaces common in deep learning. We analyse these approximations theoretically and evaluate them experimentally both directly and end-to-end as a component for real-world applications. Using our approximations for unsupervised word embedding alignment enables us to speed up a state-of-the-art method by a factor of 3 while also improving the accuracy by 3.1 percentage points without any additional model changes. For graph distance regression we propose the graph transport network (GTN), which combines graph neural networks (GNNs) with enhanced Sinkhorn. GTN outcompetes previous models by 48% and still scales log-linearly in the number of nodes.

GemNet: Universal Directional Graph Neural Networks for Molecules

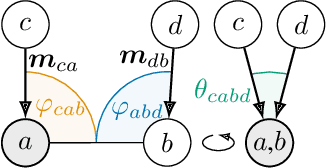
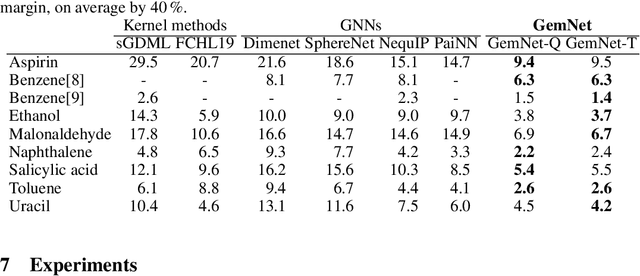
Effectively predicting molecular interactions has the potential to accelerate molecular dynamics by multiple orders of magnitude and thus revolutionize chemical simulations. Graph neural networks (GNNs) have recently shown great successes for this task, overtaking classical methods based on fixed molecular kernels. However, they still appear very limited from a theoretical perspective, since regular GNNs cannot distinguish certain types of graphs. In this work we close this gap between theory and practice. We show that GNNs with directed edge embeddings and two-hop message passing are indeed universal approximators for predictions that are invariant to global rotation and translation, and equivariant to permutation. We then leverage these insights and multiple structural improvements to propose the geometric message passing neural network (GemNet). We demonstrate the benefits of the proposed changes in multiple ablation studies. GemNet outperforms previous models on the COLL and MD17 molecular dynamics datasets by 34% and 40%, performing especially well on the most challenging molecules.

Fast and Uncertainty-Aware Directional Message Passing for Non-Equilibrium Molecules

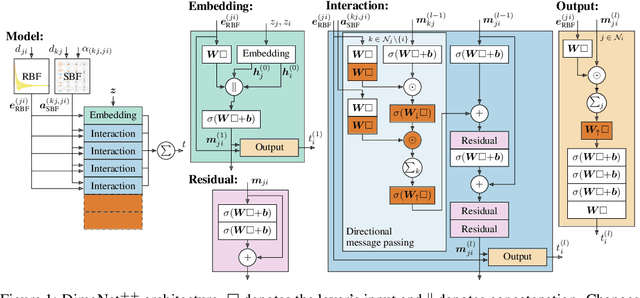
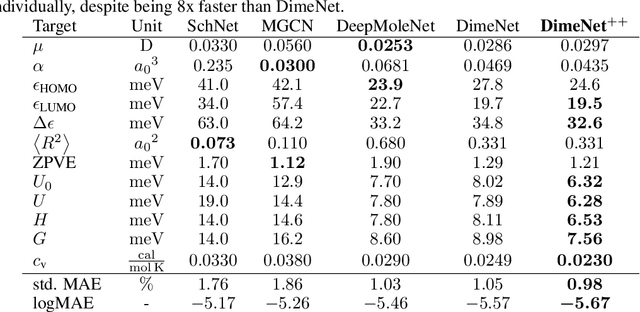
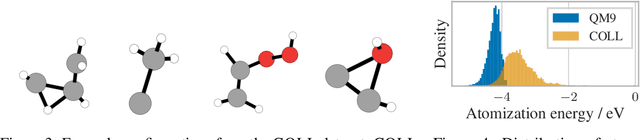
Many important tasks in chemistry revolve around molecules during reactions. This requires predictions far from the equilibrium, while most recent work in machine learning for molecules has been focused on equilibrium or near-equilibrium states. In this paper we aim to extend this scope in three ways. First, we propose the DimeNet++ model, which is 8x faster and 10% more accurate than the original DimeNet on the QM9 benchmark of equilibrium molecules. Second, we validate DimeNet++ on highly reactive molecules by developing the challenging COLL dataset, which contains distorted configurations of small molecules during collisions. Finally, we investigate ensembling and mean-variance estimation for uncertainty quantification with the goal of accelerating the exploration of the vast space of non-equilibrium structures. Our DimeNet++ implementation as well as the COLL dataset are available online.

Efficient Robustness Certificates for Discrete Data: Sparsity-Aware Randomized Smoothing for Graphs, Images and More

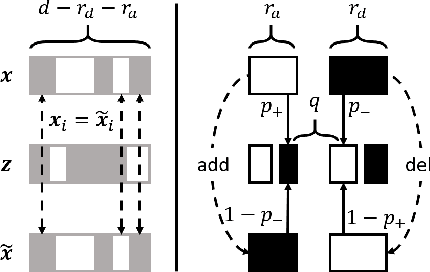
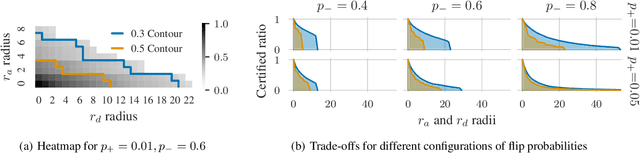
Existing techniques for certifying the robustness of models for discrete data either work only for a small class of models or are general at the expense of efficiency or tightness. Moreover, they do not account for sparsity in the input which, as our findings show, is often essential for obtaining non-trivial guarantees. We propose a model-agnostic certificate based on the randomized smoothing framework which subsumes earlier work and is tight, efficient, and sparsity-aware. Its computational complexity does not depend on the number of discrete categories or the dimension of the input (e.g. the graph size), making it highly scalable. We show the effectiveness of our approach on a wide variety of models, datasets, and tasks -- specifically highlighting its use for Graph Neural Networks. So far, obtaining provable guarantees for GNNs has been difficult due to the discrete and non-i.i.d. nature of graph data. Our method can certify any GNN and handles perturbations to both the graph structure and the node attributes.

Scaling Graph Neural Networks with Approximate PageRank

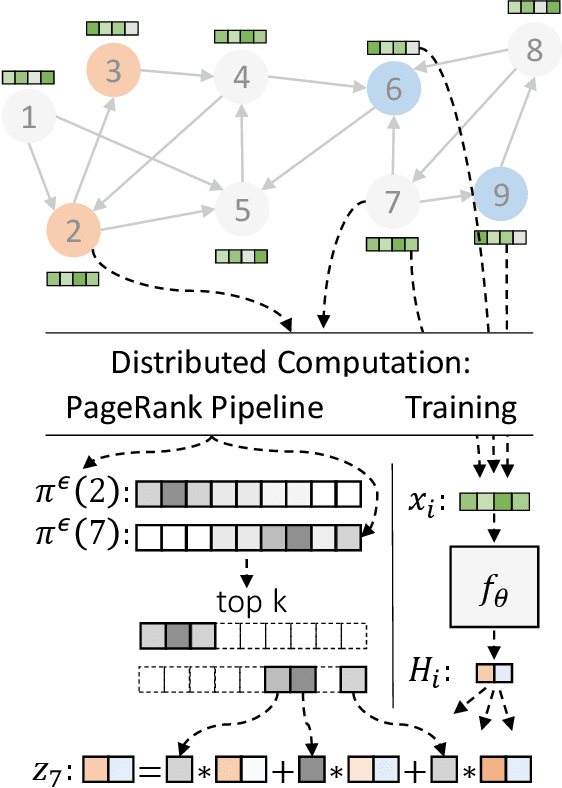
Graph neural networks (GNNs) have emerged as a powerful approach for solving many network mining tasks. However, learning on large graphs remains a challenge - many recently proposed scalable GNN approaches rely on an expensive message-passing procedure to propagate information through the graph. We present the PPRGo model which utilizes an efficient approximation of information diffusion in GNNs resulting in significant speed gains while maintaining state-of-the-art prediction performance. In addition to being faster, PPRGo is inherently scalable, and can be trivially parallelized for large datasets like those found in industry settings. We demonstrate that PPRGo outperforms baselines in both distributed and single-machine training environments on a number of commonly used academic graphs. To better analyze the scalability of large-scale graph learning methods, we introduce a novel benchmark graph with 12.4 million nodes, 173 million edges, and 2.8 million node features. We show that training PPRGo from scratch and predicting labels for all nodes in this graph takes under 2 minutes on a single machine, far outpacing other baselines on the same graph. We discuss the practical application of PPRGo to solve large-scale node classification problems at Google.

Directional Message Passing for Molecular Graphs

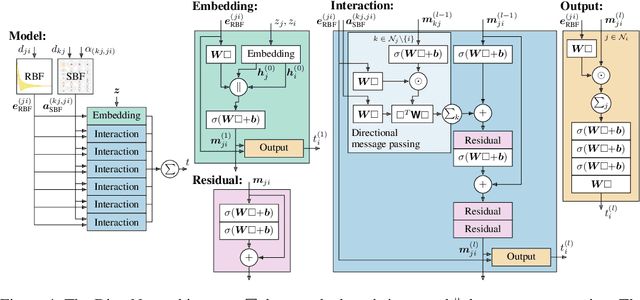
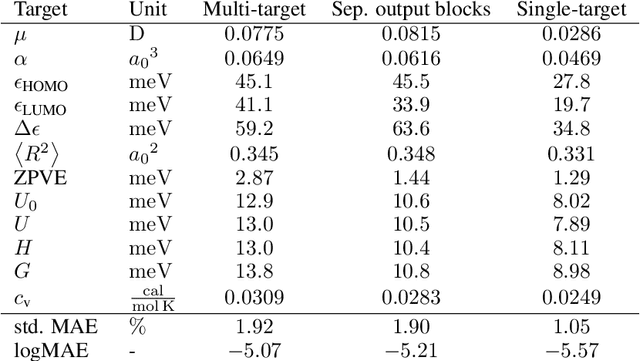
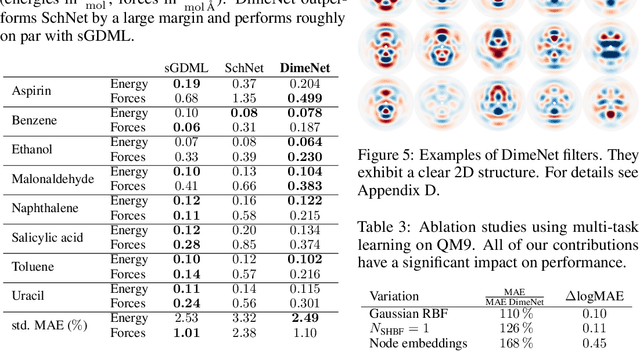
Graph neural networks have recently achieved great successes in predicting quantum mechanical properties of molecules. These models represent a molecule as a graph using only the distance between atoms (nodes). They do not, however, consider the spatial direction from one atom to another, despite directional information playing a central role in empirical potentials for molecules, e.g. in angular potentials. To alleviate this limitation we propose directional message passing, in which we embed the messages passed between atoms instead of the atoms themselves. Each message is associated with a direction in coordinate space. These directional message embeddings are rotationally equivariant since the associated directions rotate with the molecule. We propose a message passing scheme analogous to belief propagation, which uses the directional information by transforming messages based on the angle between them. Additionally, we use spherical Bessel functions and spherical harmonics to construct theoretically well-founded, orthogonal representations that achieve better performance than the currently prevalent Gaussian radial basis representations while using fewer than 1/4 of the parameters. We leverage these innovations to construct the directional message passing neural network (DimeNet). DimeNet outperforms previous GNNs on average by 76% on MD17 and by 31% on QM9. Our implementation is available online.

Diffusion Improves Graph Learning

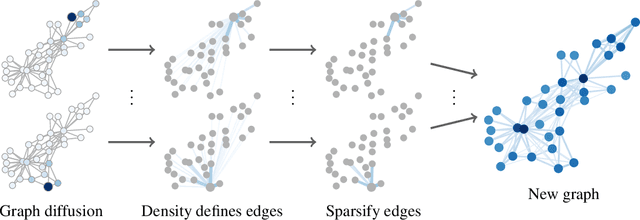
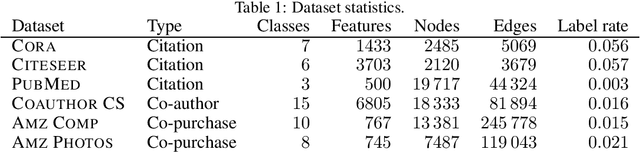
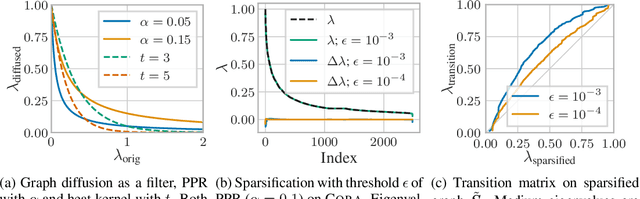
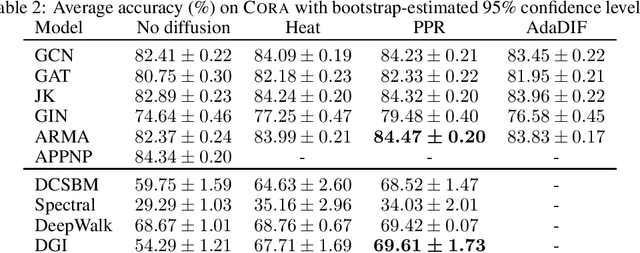
Graph convolution is the core of most Graph Neural Networks (GNNs) and usually approximated by message passing between direct (one-hop) neighbors. In this work, we remove the restriction of using only the direct neighbors by introducing a powerful, yet spatially localized graph convolution: Graph diffusion convolution (GDC). GDC leverages generalized graph diffusion, examples of which are the heat kernel and personalized PageRank. It alleviates the problem of noisy and often arbitrarily defined edges in real graphs. We show that GDC is closely related to spectral-based models and thus combines the strengths of both spatial (message passing) and spectral methods. We demonstrate that replacing message passing with graph diffusion convolution consistently leads to significant performance improvements across a wide range of models on both supervised and unsupervised tasks and a variety of datasets. Furthermore, GDC is not limited to GNNs but can trivially be combined with any graph-based model or algorithm (e.g. spectral clustering) without requiring any changes to the latter or affecting its computational complexity. Our implementation is available online.

Personalized Embedding Propagation: Combining Neural Networks on Graphs with Personalized PageRank

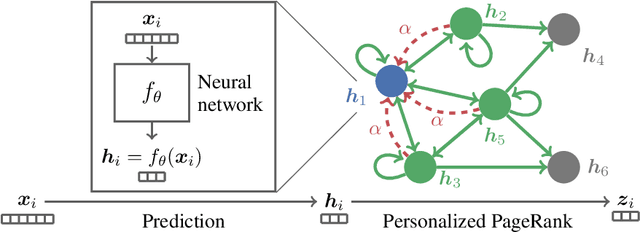
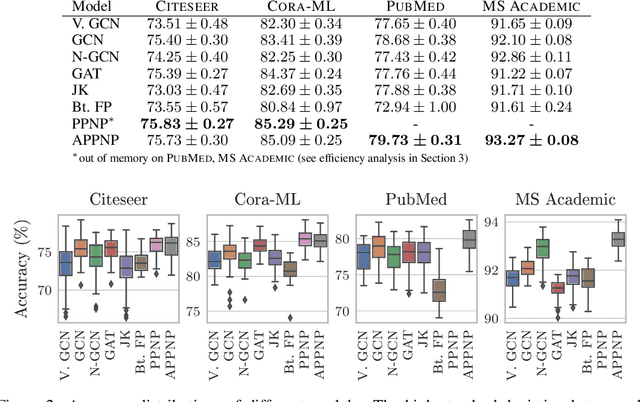
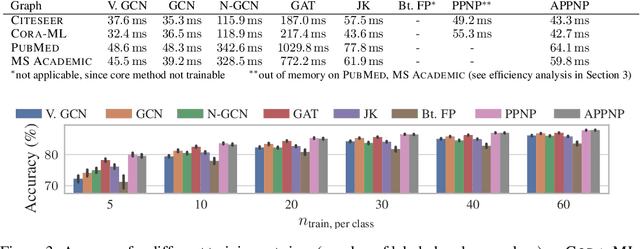
Neural message passing algorithms for semi-supervised classification on graphs have recently achieved great success. However, these methods only consider nodes that are a few propagation steps away and the size of this utilized neighborhood cannot be easily extended. In this paper, we use the relationship between graph convolutional networks (GCN) and PageRank to derive an improved propagation scheme based on personalized PageRank. We utilize this propagation procedure to construct personalized embedding propagation (PEP) and its approximation, PEP$_\text{A}$. Our model's training time is on par or faster and its number of parameters on par or lower than previous models. It leverages a large, adjustable neighborhood for classification and can be combined with any neural network. We show that this model outperforms several recently proposed methods for semi-supervised classification on multiple graphs in the most thorough study done so far for GCN-like models.