Efficient Robustness Certificates for Discrete Data: Sparsity-Aware Randomized Smoothing for Graphs, Images and More
Paper and Code
Aug 29, 2020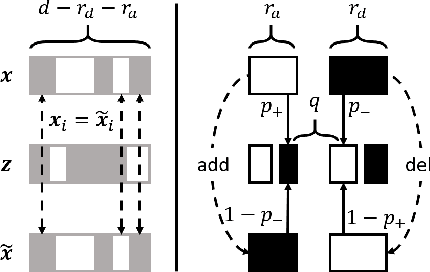

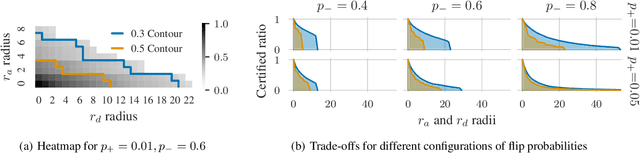

Existing techniques for certifying the robustness of models for discrete data either work only for a small class of models or are general at the expense of efficiency or tightness. Moreover, they do not account for sparsity in the input which, as our findings show, is often essential for obtaining non-trivial guarantees. We propose a model-agnostic certificate based on the randomized smoothing framework which subsumes earlier work and is tight, efficient, and sparsity-aware. Its computational complexity does not depend on the number of discrete categories or the dimension of the input (e.g. the graph size), making it highly scalable. We show the effectiveness of our approach on a wide variety of models, datasets, and tasks -- specifically highlighting its use for Graph Neural Networks. So far, obtaining provable guarantees for GNNs has been difficult due to the discrete and non-i.i.d. nature of graph data. Our method can certify any GNN and handles perturbations to both the graph structure and the node attributes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge