Communication Compression for Tensor Parallel LLM Inference

Large Language Models (LLMs) have pushed the frontier of artificial intelligence but are comprised of hundreds of billions of parameters and operations. For faster inference latency, LLMs are deployed on multiple hardware accelerators through various Model Parallelism strategies. Our paper looks into the details on one such strategy - Tensor Parallel - and proposes to reduce latency by compressing inter-accelerator communication. We leverage fine grained quantization techniques to compress selected activations by 3.5 - 4.5x. Our proposed method leads up to 2x reduction of time-to-first-token (TTFT) with negligible model performance degradation.

Generative Diffusion for 3D Turbulent Flows

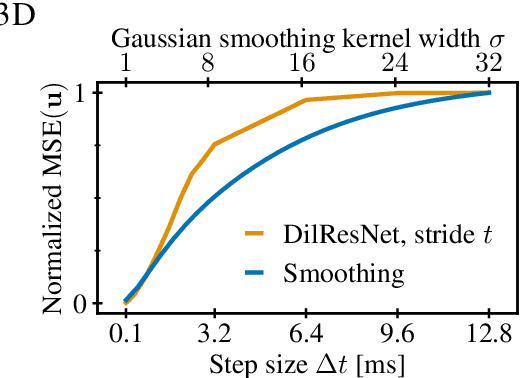
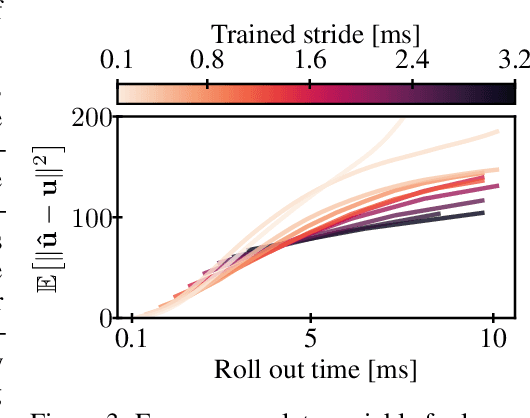
Turbulent flows are well known to be chaotic and hard to predict; however, their dynamics differ between two and three dimensions. While 2D turbulence tends to form large, coherent structures, in three dimensions vortices cascade to smaller and smaller scales. This cascade creates many fast-changing, small-scale structures and amplifies the unpredictability, making regression-based methods infeasible. We propose the first generative model for forced turbulence in arbitrary 3D geometries and introduce a sample quality metric for turbulent flows based on the Wasserstein distance of the generated velocity-vorticity distribution. In several experiments, we show that our generative diffusion model circumvents the unpredictability of turbulent flows and produces high-quality samples based solely on geometric information. Furthermore, we demonstrate that our model beats an industrial-grade numerical solver in the time to generate a turbulent flow field from scratch by an order of magnitude.