Felix Ambellan
Sasaki Metric for Spline Models of Manifold-Valued Trajectories
Mar 30, 2023



Abstract:We propose a generic spatiotemporal framework to analyze manifold-valued measurements, which allows for employing an intrinsic and computationally efficient Riemannian hierarchical model. Particularly, utilizing regression, we represent discrete trajectories in a Riemannian manifold by composite B\' ezier splines, propose a natural metric induced by the Sasaki metric to compare the trajectories, and estimate average trajectories as group-wise trends. We evaluate our framework in comparison to state-of-the-art methods within qualitative and quantitative experiments on hurricane tracks. Notably, our results demonstrate the superiority of spline-based approaches for an intensity classification of the tracks.
Landmark-free Statistical Shape Modeling via Neural Flow Deformations
Sep 14, 2022

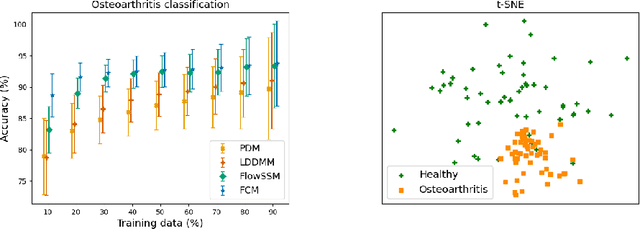
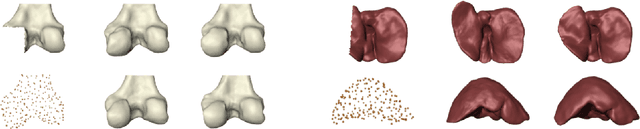
Abstract:Statistical shape modeling aims at capturing shape variations of an anatomical structure that occur within a given population. Shape models are employed in many tasks, such as shape reconstruction and image segmentation, but also shape generation and classification. Existing shape priors either require dense correspondence between training examples or lack robustness and topological guarantees. We present FlowSSM, a novel shape modeling approach that learns shape variability without requiring dense correspondence between training instances. It relies on a hierarchy of continuous deformation flows, which are parametrized by a neural network. Our model outperforms state-of-the-art methods in providing an expressive and robust shape prior for distal femur and liver. We show that the emerging latent representation is discriminative by separating healthy from pathological shapes. Ultimately, we demonstrate its effectiveness on two shape reconstruction tasks from partial data. Our source code is publicly available (https://github.com/davecasp/flowssm).
Rigid Motion Invariant Statistical Shape Modeling based on Discrete Fundamental Forms
Nov 05, 2021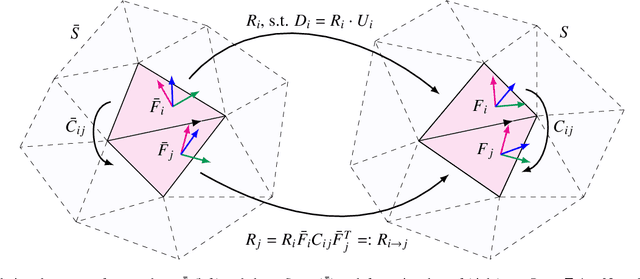

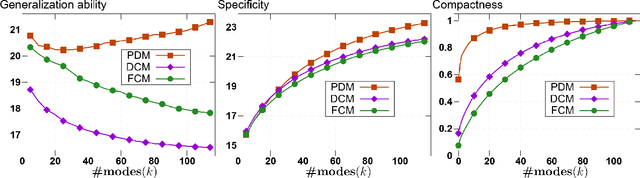
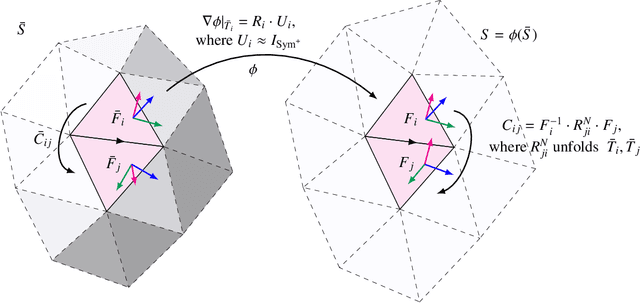
Abstract:We present a novel approach for nonlinear statistical shape modeling that is invariant under Euclidean motion and thus alignment-free. By analyzing metric distortion and curvature of shapes as elements of Lie groups in a consistent Riemannian setting, we construct a framework that reliably handles large deformations. Due to the explicit character of Lie group operations, our non-Euclidean method is very efficient allowing for fast and numerically robust processing. This facilitates Riemannian analysis of large shape populations accessible through longitudinal and multi-site imaging studies providing increased statistical power. Additionally, as planar configurations form a submanifold in shape space, our representation allows for effective estimation of quasi-isometric surfaces flattenings. We evaluate the performance of our model w.r.t. shape-based classification of hippocampus and femur malformations due to Alzheimer's disease and osteoarthritis, respectively. In particular, we outperform state-of-the-art classifiers based on geometric deep learning as well as statistical shape modeling especially in presence of sparse training data. We evaluate the performance of our model w.r.t. shape-based classification of pathological malformations of the human knee and show that it outperforms the standard Euclidean as well as a recent nonlinear approach especially in presence of sparse training data. To provide insight into the model's ability of capturing biological shape variability, we carry out an analysis of specificity and generalization ability.
Geodesic B-Score for Improved Assessment of Knee Osteoarthritis
Mar 12, 2021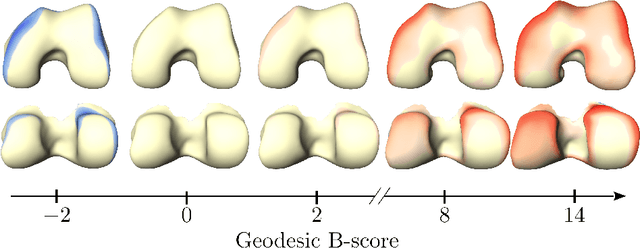

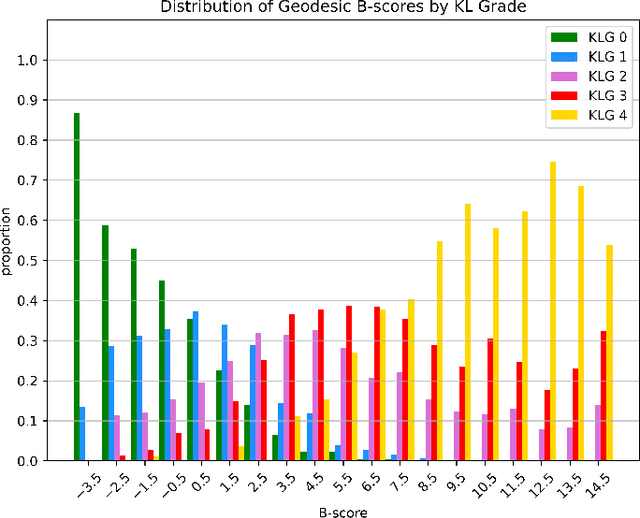
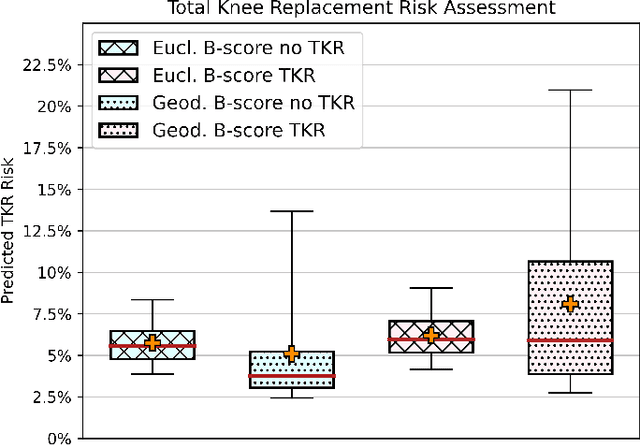
Abstract:Three-dimensional medical imaging enables detailed understanding of osteoarthritis structural status. However, there remains a vast need for automatic, thus, reader-independent measures that provide reliable assessment of subject-specific clinical outcomes. To this end, we derive a consistent generalization of the recently proposed B-score to Riemannian shape spaces. We further present an algorithmic treatment yielding simple, yet efficient computations allowing for analysis of large shape populations with several thousand samples. Our intrinsic formulation exhibits improved discrimination ability over its Euclidean counterpart, which we demonstrate for predictive validity on assessing risks of total knee replacement. This result highlights the potential of the geodesic B-score to enable improved personalized assessment and stratification for interventions.
VerSe: A Vertebrae Labelling and Segmentation Benchmark
Jan 24, 2020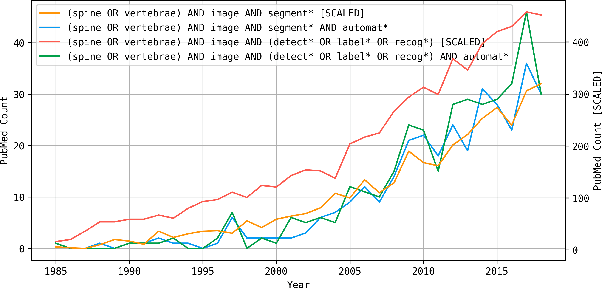
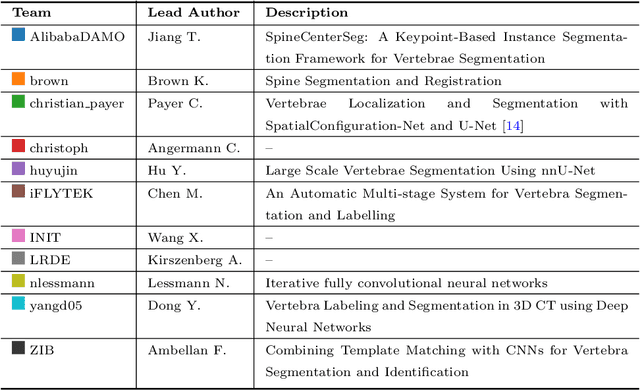
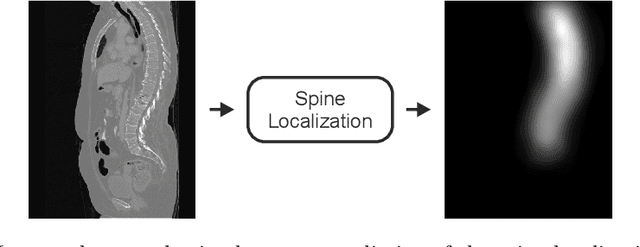
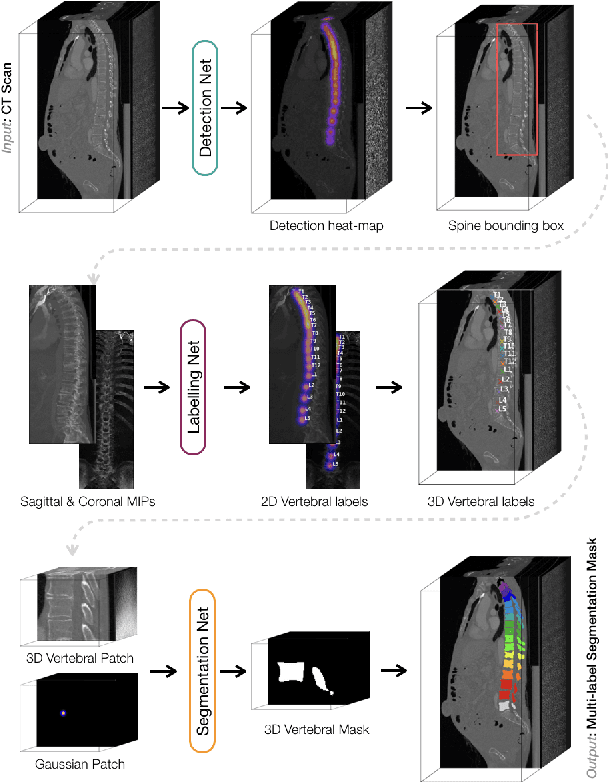
Abstract:In this paper we report the challenge set-up and results of the Large Scale Vertebrae Segmentation Challenge (VerSe) organized in conjunction with the MICCAI 2019. The challenge consisted of two tasks, vertebrae labelling and vertebrae segmentation. For this a total of 160 multidetector CT scan cohort closely resembling clinical setting was prepared and was annotated at a voxel-level by a human-machine hybrid algorithm. In this paper we also present the annotation protocol and the algorithm that aided the medical experts in the annotation process. Eleven fully automated algorithms were benchmarked on this data with the best performing algorithm achieving a vertebrae identification rate of 95% and a Dice coefficient of 90%. VerSe'19 is an open-call challenge at its image data along with the annotations and evaluation tools will continue to be publicly accessible through its online portal.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge