Bi-invariant Geodesic Regression with Data from the Osteoarthritis Initiative

Many phenomena are naturally characterized by measuring continuous transformations such as shape changes in medicine or articulated systems in robotics. Modeling the variability in such datasets requires performing statistics on Lie groups, that is, manifolds carrying an additional group structure. As the Lie group captures the symmetries in the data, it is essential from a theoretical and practical perspective to ask for statistical methods that respect these symmetries; this way they are insensitive to confounding effects, e.g., due to the choice of reference coordinate systems. In this work, we investigate geodesic regression -- a generalization of linear regression originally derived for Riemannian manifolds. While Lie groups can be endowed with Riemannian metrics, these are generally incompatible with the group structure. We develop a non-metric estimator using an affine connection setting. It captures geodesic relationships respecting the symmetries given by left and right translations. For its computation, we propose an efficient fixed point algorithm requiring simple differential expressions that can be calculated through automatic differentiation. We perform experiments on a synthetic example and evaluate our method on an open-access, clinical dataset studying knee joint configurations under the progression of osteoarthritis.

Manifold GCN: Diffusion-based Convolutional Neural Network for Manifold-valued Graphs

We propose two graph neural network layers for graphs with features in a Riemannian manifold. First, based on a manifold-valued graph diffusion equation, we construct a diffusion layer that can be applied to an arbitrary number of nodes and graph connectivity patterns. Second, we model a tangent multilayer perceptron by transferring ideas from the vector neuron framework to our general setting. Both layers are equivariant with respect to node permutations and isometries of the feature manifold. These properties have been shown to lead to a beneficial inductive bias in many deep learning tasks. Numerical examples on synthetic data as well as on triangle meshes of the right hippocampus to classify Alzheimer's disease demonstrate the very good performance of our layers.

Intrinsic shape analysis in archaeology: A case study on ancient sundials

This paper explores a novel mathematical approach to extract archaeological insights from ensembles of similar artifact shapes. We show that by considering all the shape information in a find collection, it is possible to identify shape patterns that would be difficult to discern by considering the artifacts individually or by classifying shapes into predefined archaeological types and analyzing the associated distinguishing characteristics. Recently, series of high-resolution digital representations of artifacts have become available, and we explore their potential on a set of 3D models of ancient Greek and Roman sundials, with the aim of providing alternatives to the traditional archaeological method of ``trend extraction by ordination'' (typology). In the proposed approach, each 3D shape is represented as a point in a shape space -- a high-dimensional, curved, non-Euclidean space. By performing regression in shape space, we find that for Roman sundials, the bend of the sundials' shadow-receiving surface changes with the location's latitude. This suggests that, apart from the inscribed hour lines, also a sundial's shape was adjusted to the place of installation. As an example of more advanced inference, we use the identified trend to infer the latitude at which a sundial, whose installation location is unknown, was placed. We also derive a novel method for differentiated morphological trend assertion, building upon and extending the theory of geometric statistics and shape analysis. Specifically, we present a regression-based method for statistical normalization of shapes that serves as a means of disentangling parameter-dependent effects (trends) and unexplained variability.

Sasaki Metric for Spline Models of Manifold-Valued Trajectories

We propose a generic spatiotemporal framework to analyze manifold-valued measurements, which allows for employing an intrinsic and computationally efficient Riemannian hierarchical model. Particularly, utilizing regression, we represent discrete trajectories in a Riemannian manifold by composite B\' ezier splines, propose a natural metric induced by the Sasaki metric to compare the trajectories, and estimate average trajectories as group-wise trends. We evaluate our framework in comparison to state-of-the-art methods within qualitative and quantitative experiments on hurricane tracks. Notably, our results demonstrate the superiority of spline-based approaches for an intensity classification of the tracks.

Predicting Shape Development: a Riemannian Method

Predicting the future development of an anatomical shape from a single baseline is an important but difficult problem to solve. Research has shown that it should be tackled in curved shape spaces, as (e.g., disease-related) shape changes frequently expose nonlinear characteristics. We thus propose a novel prediction method that encodes the whole shape in a Riemannian shape space. It then learns a simple prediction technique that is founded on statistical hierarchical modelling of longitudinal training data. It is fully automatic, which makes it stand out in contrast to parameter-rich state-of-the-art methods. When applied to predict the future development of the shape of right hippocampi under Alzheimer's disease, it outperforms deep learning supported variants and achieves results on par with state-of-the-art.

Predicting cognitive scores with graph neural networks through sample selection learning

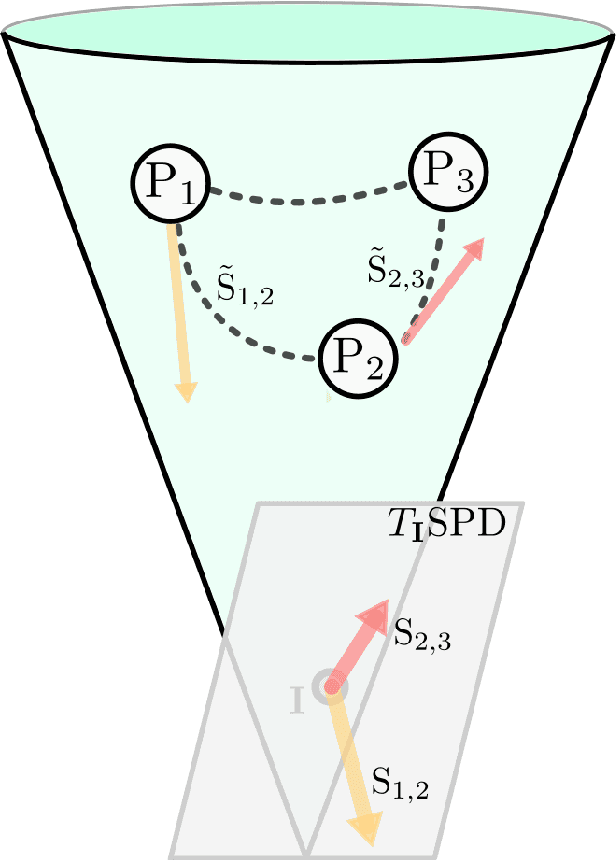
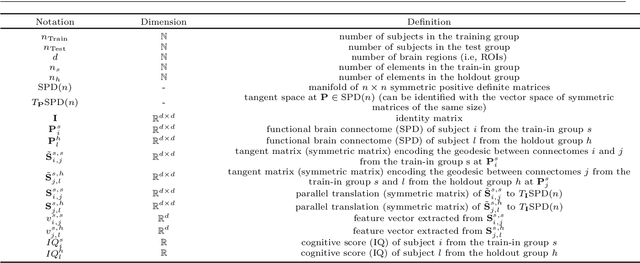
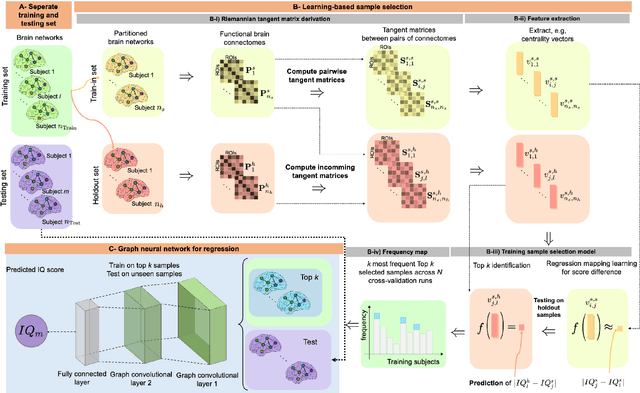
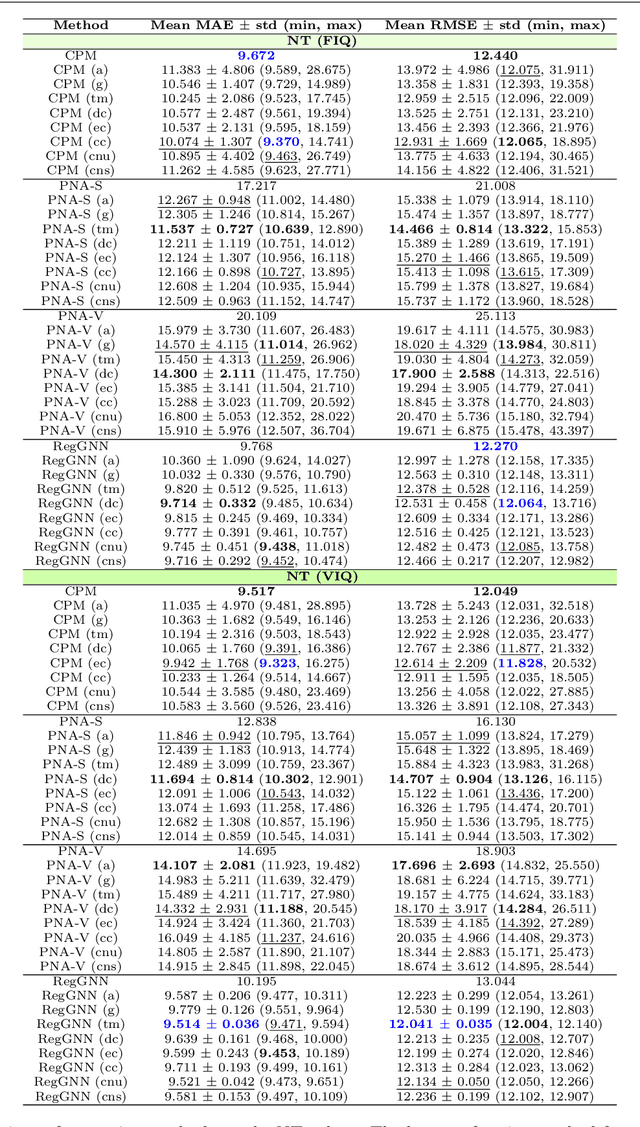
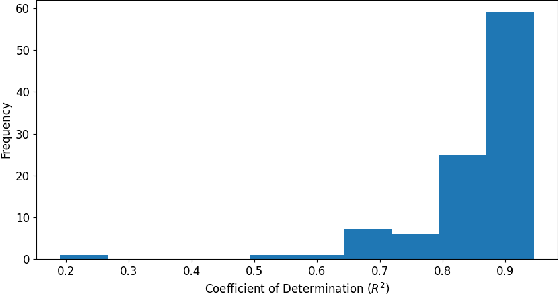
Analyzing the relation between intelligence and neural activity is of the utmost importance in understanding the working principles of the human brain in health and disease. In existing literature, functional brain connectomes have been used successfully to predict cognitive measures such as intelligence quotient (IQ) scores in both healthy and disordered cohorts using machine learning models. However, existing methods resort to flattening the brain connectome (i.e., graph) through vectorization which overlooks its topological properties. To address this limitation and inspired from the emerging graph neural networks (GNNs), we design a novel regression GNN model (namely RegGNN) for predicting IQ scores from brain connectivity. On top of that, we introduce a novel, fully modular sample selection method to select the best samples to learn from for our target prediction task. However, since such deep learning architectures are computationally expensive to train, we further propose a \emph{learning-based sample selection} method that learns how to choose the training samples with the highest expected predictive power on unseen samples. For this, we capitalize on the fact that connectomes (i.e., their adjacency matrices) lie in the symmetric positive definite (SPD) matrix cone. Our results on full-scale and verbal IQ prediction outperforms comparison methods in autism spectrum disorder cohorts and achieves a competitive performance for neurotypical subjects using 3-fold cross-validation. Furthermore, we show that our sample selection approach generalizes to other learning-based methods, which shows its usefulness beyond our GNN architecture.