Learning Equivariant Non-Local Electron Density Functionals

The accuracy of density functional theory hinges on the approximation of non-local contributions to the exchange-correlation (XC) functional. To date, machine-learned and human-designed approximations suffer from insufficient accuracy, limited scalability, or dependence on costly reference data. To address these issues, we introduce Equivariant Graph Exchange Correlation (EG-XC), a novel non-local XC functional based on equivariant graph neural networks. EG-XC combines semi-local functionals with a non-local feature density parametrized by an equivariant nuclei-centered point cloud representation of the electron density to capture long-range interactions. By differentiating through a self-consistent field solver, we train EG-XC requiring only energy targets. In our empirical evaluation, we find EG-XC to accurately reconstruct `gold-standard' CCSD(T) energies on MD17. On out-of-distribution conformations of 3BPA, EG-XC reduces the relative MAE by 35% to 50%. Remarkably, EG-XC excels in data efficiency and molecular size extrapolation on QM9, matching force fields trained on 5 times more and larger molecules. On identical training sets, EG-XC yields on average 51% lower MAEs.

Lift Your Molecules: Molecular Graph Generation in Latent Euclidean Space

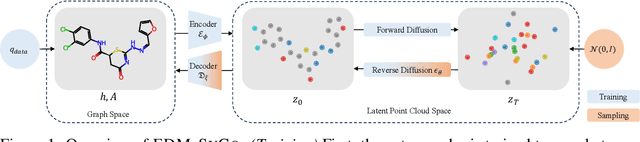
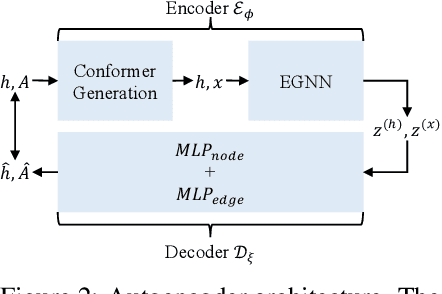
We introduce a new framework for molecular graph generation with 3D molecular generative models. Our Synthetic Coordinate Embedding (SyCo) framework maps molecular graphs to Euclidean point clouds via synthetic conformer coordinates and learns the inverse map using an E(n)-Equivariant Graph Neural Network (EGNN). The induced point cloud-structured latent space is well-suited to apply existing 3D molecular generative models. This approach simplifies the graph generation problem - without relying on molecular fragments nor autoregressive decoding - into a point cloud generation problem followed by node and edge classification tasks. Further, we propose a novel similarity-constrained optimization scheme for 3D diffusion models based on inpainting and guidance. As a concrete implementation of our framework, we develop EDM-SyCo based on the E(3) Equivariant Diffusion Model (EDM). EDM-SyCo achieves state-of-the-art performance in distribution learning of molecular graphs, outperforming the best non-autoregressive methods by more than 30% on ZINC250K and 16% on the large-scale GuacaMol dataset while improving conditional generation by up to 3.9 times.

Neural Pfaffians: Solving Many Many-Electron Schrödinger Equations

Neural wave functions accomplished unprecedented accuracies in approximating the ground state of many-electron systems, though at a high computational cost. Recent works proposed amortizing the cost by learning generalized wave functions across different structures and compounds instead of solving each problem independently. Enforcing the permutation antisymmetry of electrons in such generalized neural wave functions remained challenging as existing methods require discrete orbital selection via non-learnable hand-crafted algorithms. This work tackles the problem by defining overparametrized, fully learnable neural wave functions suitable for generalization across molecules. We achieve this by relying on Pfaffians rather than Slater determinants. The Pfaffian allows us to enforce the antisymmetry on arbitrary electronic systems without any constraint on electronic spin configurations or molecular structure. Our empirical evaluation finds that a single neural Pfaffian calculates the ground state and ionization energies with chemical accuracy across various systems. On the TinyMol dataset, we outperform the `gold-standard' CCSD(T) CBS reference energies by 1.9m$E_h$ and reduce energy errors compared to previous generalized neural wave functions by up to an order of magnitude.

On Representing Electronic Wave Functions with Sign Equivariant Neural Networks

Recent neural networks demonstrated impressively accurate approximations of electronic ground-state wave functions. Such neural networks typically consist of a permutation-equivariant neural network followed by a permutation-antisymmetric operation to enforce the electronic exchange symmetry. While accurate, such neural networks are computationally expensive. In this work, we explore the flipped approach, where we first compute antisymmetric quantities based on the electronic coordinates and then apply sign equivariant neural networks to preserve the antisymmetry. While this approach promises acceleration thanks to the lower-dimensional representation, we demonstrate that it reduces to a Jastrow factor, a commonly used permutation-invariant multiplicative factor in the wave function. Our empirical results support this further, finding little to no improvements over baselines. We conclude with neither theoretical nor empirical advantages of sign equivariant functions for representing electronic wave functions within the evaluation of this work.

Artificial Intelligence for Science in Quantum, Atomistic, and Continuum Systems

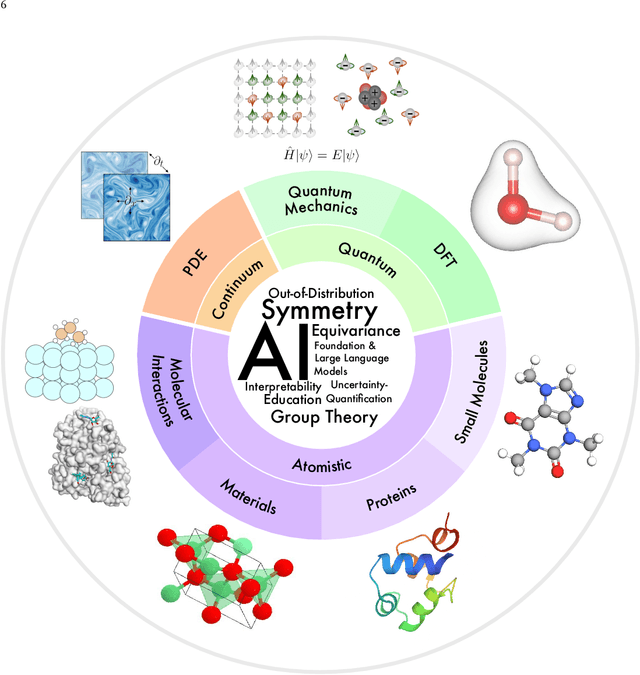
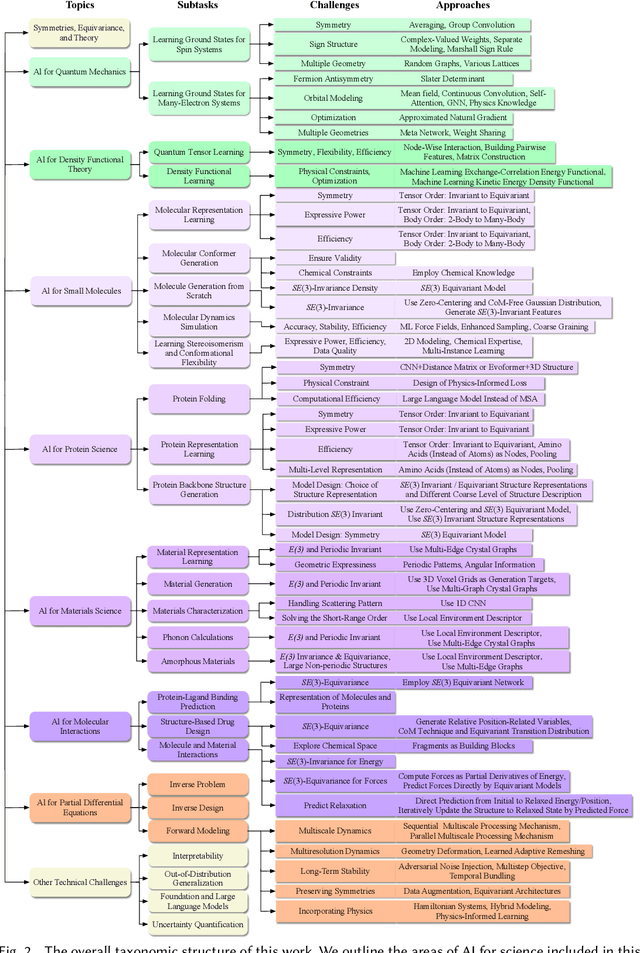
Advances in artificial intelligence (AI) are fueling a new paradigm of discoveries in natural sciences. Today, AI has started to advance natural sciences by improving, accelerating, and enabling our understanding of natural phenomena at a wide range of spatial and temporal scales, giving rise to a new area of research known as AI for science (AI4Science). Being an emerging research paradigm, AI4Science is unique in that it is an enormous and highly interdisciplinary area. Thus, a unified and technical treatment of this field is needed yet challenging. This paper aims to provide a technically thorough account of a subarea of AI4Science; namely, AI for quantum, atomistic, and continuum systems. These areas aim at understanding the physical world from the subatomic (wavefunctions and electron density), atomic (molecules, proteins, materials, and interactions), to macro (fluids, climate, and subsurface) scales and form an important subarea of AI4Science. A unique advantage of focusing on these areas is that they largely share a common set of challenges, thereby allowing a unified and foundational treatment. A key common challenge is how to capture physics first principles, especially symmetries, in natural systems by deep learning methods. We provide an in-depth yet intuitive account of techniques to achieve equivariance to symmetry transformations. We also discuss other common technical challenges, including explainability, out-of-distribution generalization, knowledge transfer with foundation and large language models, and uncertainty quantification. To facilitate learning and education, we provide categorized lists of resources that we found to be useful. We strive to be thorough and unified and hope this initial effort may trigger more community interests and efforts to further advance AI4Science.

Uncertainty Estimation for Molecules: Desiderata and Methods

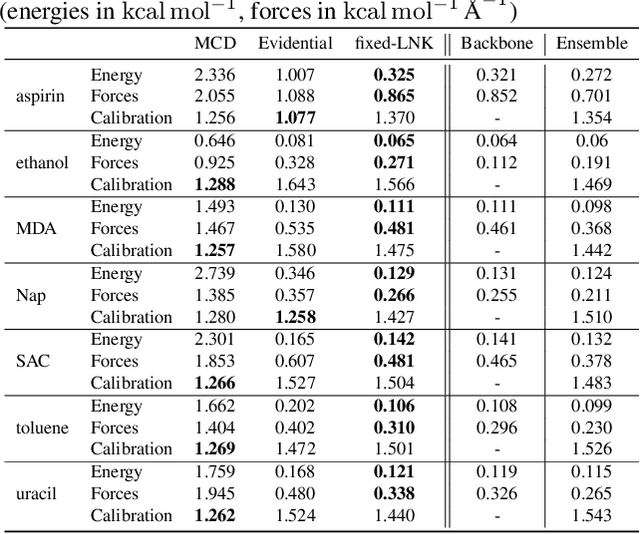
Graph Neural Networks (GNNs) are promising surrogates for quantum mechanical calculations as they establish unprecedented low errors on collections of molecular dynamics (MD) trajectories. Thanks to their fast inference times they promise to accelerate computational chemistry applications. Unfortunately, despite low in-distribution (ID) errors, such GNNs might be horribly wrong for out-of-distribution (OOD) samples. Uncertainty estimation (UE) may aid in such situations by communicating the model's certainty about its prediction. Here, we take a closer look at the problem and identify six key desiderata for UE in molecular force fields, three 'physics-informed' and three 'application-focused' ones. To overview the field, we survey existing methods from the field of UE and analyze how they fit to the set desiderata. By our analysis, we conclude that none of the previous works satisfies all criteria. To fill this gap, we propose Localized Neural Kernel (LNK) a Gaussian Process (GP)-based extension to existing GNNs satisfying the desiderata. In our extensive experimental evaluation, we test four different UE with three different backbones and two datasets. In out-of-equilibrium detection, we find LNK yielding up to 2.5 and 2.1 times lower errors in terms of AUC-ROC score than dropout or evidential regression-based methods while maintaining high predictive performance.

Ewald-based Long-Range Message Passing for Molecular Graphs

Neural architectures that learn potential energy surfaces from molecular data have undergone fast improvement in recent years. A key driver of this success is the Message Passing Neural Network (MPNN) paradigm. Its favorable scaling with system size partly relies upon a spatial distance limit on messages. While this focus on locality is a useful inductive bias, it also impedes the learning of long-range interactions such as electrostatics and van der Waals forces. To address this drawback, we propose Ewald message passing: a nonlocal Fourier space scheme which limits interactions via a cutoff on frequency instead of distance, and is theoretically well-founded in the Ewald summation method. It can serve as an augmentation on top of existing MPNN architectures as it is computationally cheap and agnostic to other architectural details. We test the approach with four baseline models and two datasets containing diverse periodic (OC20) and aperiodic structures (OE62). We observe robust improvements in energy mean absolute errors across all models and datasets, averaging 10% on OC20 and 16% on OE62. Our analysis shows an outsize impact of these improvements on structures with high long-range contributions to the ground truth energy.

Generalizing Neural Wave Functions

Recent neural network-based wave functions have achieved state-of-the-art accuracies in modeling ab-initio ground-state potential energy surface. However, these networks can only solve different spatial arrangements of the same set of atoms. To overcome this limitation, we present Graph-learned Orbital Embeddings (Globe), a neural network-based reparametrization method that can adapt neural wave functions to different molecules. We achieve this by combining a localization method for molecular orbitals with spatial message-passing networks. Further, we propose a locality-driven wave function, the Molecular Oribtal Network (Moon), tailored to solving Schr\"odinger equations of different molecules jointly. In our experiments, we find Moon requiring 8 times fewer steps to converge to similar accuracies as previous methods when trained on different molecules jointly while Globe enabling the transfer from smaller to larger molecules. Further, our analysis shows that Moon converges similarly to recent transformer-based wave functions on larger molecules. In both the computational chemistry and machine learning literature, we are the first to demonstrate that a single wave function can solve the Schr\"odinger equation of molecules with different atoms jointly.

Sampling-free Inference for Ab-Initio Potential Energy Surface Networks

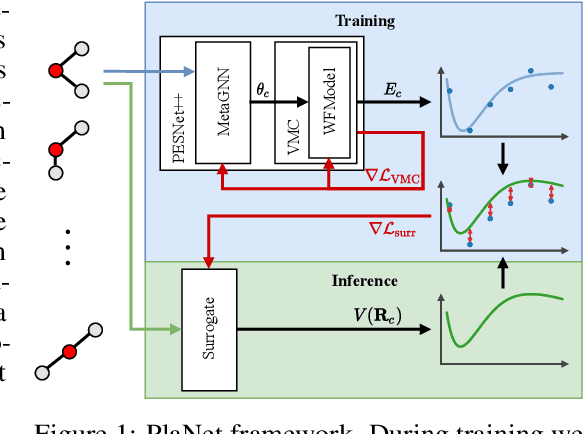
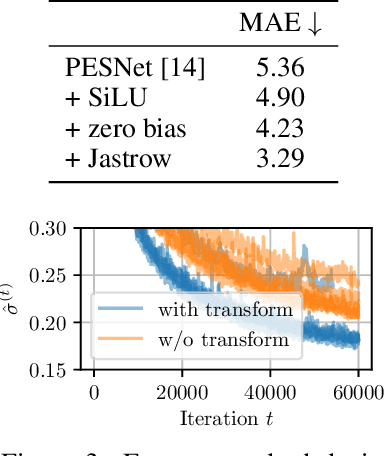
Obtaining the energy of molecular systems typically requires solving the associated Schr\"odinger equation. Unfortunately, analytical solutions only exist for single-electron systems, and accurate approximate solutions are expensive. In recent work, the potential energy surface network (PESNet) has been proposed to reduce training time by solving the Schr\"odinger equation for many geometries simultaneously. While training significantly faster, inference still required numerical integration limiting the evaluation to a few geometries. Here, we address the inference shortcomings by proposing the Potential learning from ab-initio Networks (PlaNet) framework to simultaneously train a surrogate model that avoids expensive Monte-Carlo integration and, thus, reduces inference time from minutes or even hours to milliseconds. In this way, we can accurately model high-resolution multi-dimensional energy surfaces that previously would have been unobtainable via neural wave functions. Finally, we present PESNet++, an architectural improvement to PESNet, that reduces errors by up to 39% and provides new state-of-the-art results for neural wave functions across all systems evaluated.

Ab-Initio Potential Energy Surfaces by Pairing GNNs with Neural Wave Functions

Solving the Schr\"odinger equation is key to many quantum mechanical properties. However, an analytical solution is only tractable for single-electron systems. Recently, neural networks succeeded at modelling wave functions of many-electron systems. Together with the variational Monte-Carlo (VMC) framework, this led to solutions on par with the best known classical methods. Still, these neural methods require tremendous amounts of computational resources as one has to train a separate model for each molecular geometry. In this work, we combine a Graph Neural Network (GNN) with a neural wave function to simultaneously solve the Schr\"odinger equation for multiple geometries via VMC. This enables us to model continuous subsets of the potential energy surface with a single training pass. Compared to existing state-of-the-art networks, our Potential Energy Surface Network (PESNet) speeds up training for multiple geometries by up to 40 times while matching or surpassing their accuracy. This may open the path to accurate and orders of magnitude cheaper quantum mechanical calculations.