Sampling-free Inference for Ab-Initio Potential Energy Surface Networks
Paper and Code
May 30, 2022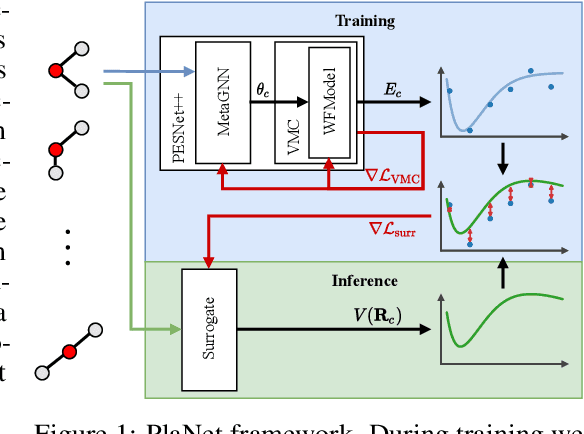

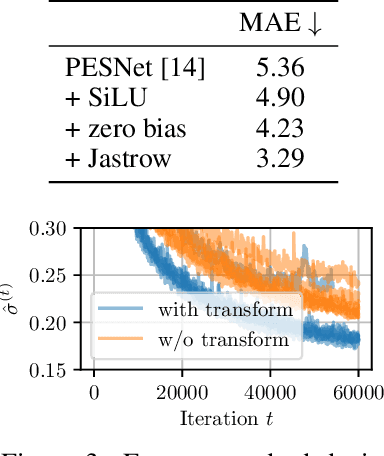
Obtaining the energy of molecular systems typically requires solving the associated Schr\"odinger equation. Unfortunately, analytical solutions only exist for single-electron systems, and accurate approximate solutions are expensive. In recent work, the potential energy surface network (PESNet) has been proposed to reduce training time by solving the Schr\"odinger equation for many geometries simultaneously. While training significantly faster, inference still required numerical integration limiting the evaluation to a few geometries. Here, we address the inference shortcomings by proposing the Potential learning from ab-initio Networks (PlaNet) framework to simultaneously train a surrogate model that avoids expensive Monte-Carlo integration and, thus, reduces inference time from minutes or even hours to milliseconds. In this way, we can accurately model high-resolution multi-dimensional energy surfaces that previously would have been unobtainable via neural wave functions. Finally, we present PESNet++, an architectural improvement to PESNet, that reduces errors by up to 39% and provides new state-of-the-art results for neural wave functions across all systems evaluated.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge