Uncertainty Estimation for Molecules: Desiderata and Methods
Paper and Code
Jun 20, 2023


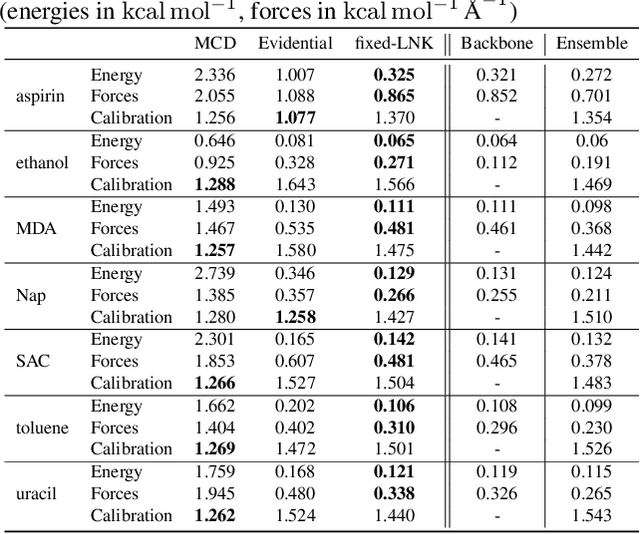
Graph Neural Networks (GNNs) are promising surrogates for quantum mechanical calculations as they establish unprecedented low errors on collections of molecular dynamics (MD) trajectories. Thanks to their fast inference times they promise to accelerate computational chemistry applications. Unfortunately, despite low in-distribution (ID) errors, such GNNs might be horribly wrong for out-of-distribution (OOD) samples. Uncertainty estimation (UE) may aid in such situations by communicating the model's certainty about its prediction. Here, we take a closer look at the problem and identify six key desiderata for UE in molecular force fields, three 'physics-informed' and three 'application-focused' ones. To overview the field, we survey existing methods from the field of UE and analyze how they fit to the set desiderata. By our analysis, we conclude that none of the previous works satisfies all criteria. To fill this gap, we propose Localized Neural Kernel (LNK) a Gaussian Process (GP)-based extension to existing GNNs satisfying the desiderata. In our extensive experimental evaluation, we test four different UE with three different backbones and two datasets. In out-of-equilibrium detection, we find LNK yielding up to 2.5 and 2.1 times lower errors in terms of AUC-ROC score than dropout or evidential regression-based methods while maintaining high predictive performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge