The sampling complexity of learning invertible residual neural networks

In recent work it has been shown that determining a feedforward ReLU neural network to within high uniform accuracy from point samples suffers from the curse of dimensionality in terms of the number of samples needed. As a consequence, feedforward ReLU neural networks are of limited use for applications where guaranteed high uniform accuracy is required. We consider the question of whether the sampling complexity can be improved by restricting the specific neural network architecture. To this end, we investigate invertible residual neural networks which are foundational architectures in deep learning and are widely employed in models that power modern generative methods. Our main result shows that the residual neural network architecture and invertibility do not help overcome the complexity barriers encountered with simpler feedforward architectures. Specifically, we demonstrate that the computational complexity of approximating invertible residual neural networks from point samples in the uniform norm suffers from the curse of dimensionality. Similar results are established for invertible convolutional Residual neural networks.

Transferable Neural Wavefunctions for Solids

Deep-Learning-based Variational Monte Carlo (DL-VMC) has recently emerged as a highly accurate approach for finding approximate solutions to the many-electron Schr\"odinger equation. Despite its favorable scaling with the number of electrons, $\mathcal{O}(n_\text{el}^{4})$, the practical value of DL-VMC is limited by the high cost of optimizing the neural network weights for every system studied. To mitigate this problem, recent research has proposed optimizing a single neural network across multiple systems, reducing the cost per system. Here we extend this approach to solids, where similar but distinct calculations using different geometries, boundary conditions, and supercell sizes are often required. We show how to optimize a single ansatz across all of these variations, reducing the required number of optimization steps by an order of magnitude. Furthermore, we exploit the transfer capabilities of a pre-trained network. We successfully transfer a network, pre-trained on 2x2x2 supercells of LiH, to 3x3x3 supercells. This reduces the number of optimization steps required to simulate the large system by a factor of 50 compared to previous work.

Sampling Complexity of Deep Approximation Spaces

While it is well-known that neural networks enjoy excellent approximation capabilities, it remains a big challenge to compute such approximations from point samples. Based on tools from Information-based complexity, recent work by Grohs and Voigtlaender [Journal of the FoCM (2023)] developed a rigorous framework for assessing this so-called "theory-to-practice gap". More precisely, in that work it is shown that there exist functions that can be approximated by neural networks with ReLU activation function at an arbitrary rate while requiring an exponentially growing (in the input dimension) number of samples for their numerical computation. The present study extends these findings by showing analogous results for the ReQU activation function.

Variational Monte Carlo on a Budget -- Fine-tuning pre-trained Neural Wavefunctions

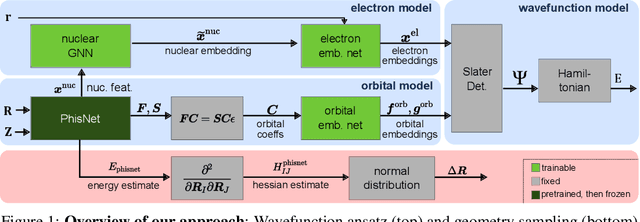
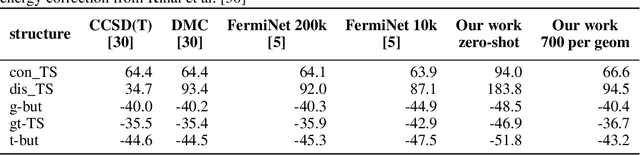
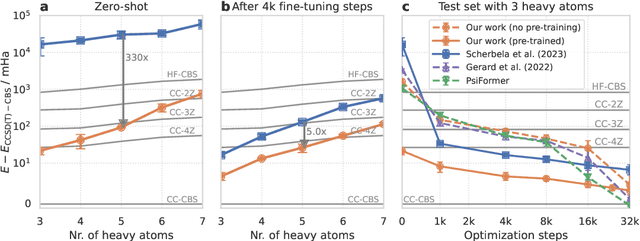
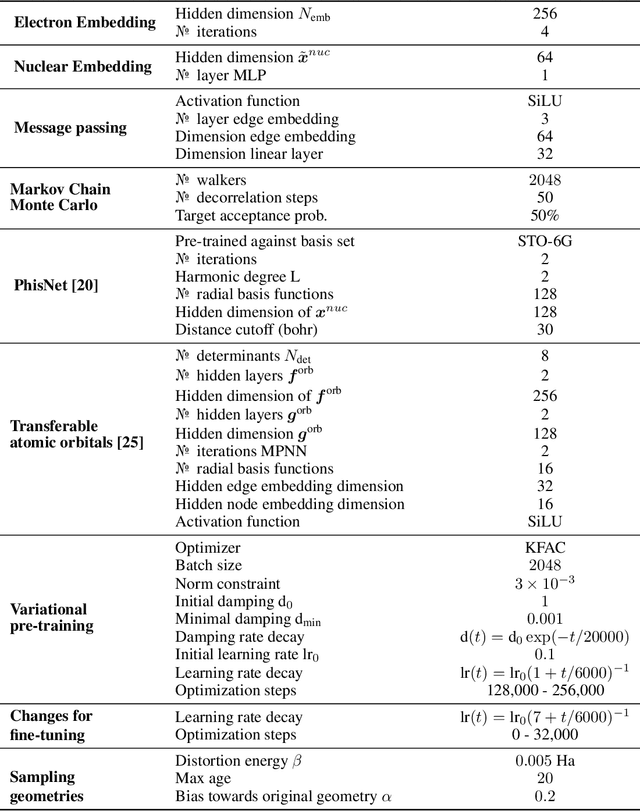
Obtaining accurate solutions to the Schr\"odinger equation is the key challenge in computational quantum chemistry. Deep-learning-based Variational Monte Carlo (DL-VMC) has recently outperformed conventional approaches in terms of accuracy, but only at large computational cost. Whereas in many domains models are trained once and subsequently applied for inference, accurate DL-VMC so far requires a full optimization for every new problem instance, consuming thousands of GPUhs even for small molecules. We instead propose a DL-VMC model which has been pre-trained using self-supervised wavefunction optimization on a large and chemically diverse set of molecules. Applying this model to new molecules without any optimization, yields wavefunctions and absolute energies that outperform established methods such as CCSD(T)-2Z. To obtain accurate relative energies, only few fine-tuning steps of this base model are required. We accomplish this with a fully end-to-end machine-learned model, consisting of an improved geometry embedding architecture and an existing SE(3)-equivariant model to represent molecular orbitals. Combining this architecture with continuous sampling of geometries, we improve zero-shot accuracy by two orders of magnitude compared to the state of the art. We extensively evaluate the accuracy, scalability and limitations of our base model on a wide variety of test systems.

FakET: Simulating Cryo-Electron Tomograms with Neural Style Transfer

Particle localization and -classification constitute two of the most fundamental problems in computational microscopy. In recent years, deep learning based approaches have been introduced for these tasks with great success. A key shortcoming of these supervised learning methods is their need for large training data sets, typically generated from particle models in conjunction with complex numerical forward models simulating the physics of transmission electron microscopes. Computer implementations of such forward models are computationally extremely demanding and limit the scope of their applicability. In this paper we propose a simple method for simulating the forward operator of an electron microscope based on additive noise and Neural Style Transfer techniques. We evaluate the method on localization and classification tasks using one of the established state-of-the-art architectures showing performance on par with the benchmark. In contrast to previous approaches, our method accelerates the data generation process by a factor of 750 while using 33 times less memory and scales well to typical transmission electron microscope detector sizes. It utilizes GPU acceleration and parallel processing. It can be used as a stand-alone method to adapt a training data set or as a data augmentation technique. The source code is available at https://gitlab.com/deepet/faket.

Towards a Foundation Model for Neural Network Wavefunctions

Deep neural networks have become a highly accurate and powerful wavefunction ansatz in combination with variational Monte Carlo methods for solving the electronic Schr\"odinger equation. However, despite their success and favorable scaling, these methods are still computationally too costly for wide adoption. A significant obstacle is the requirement to optimize the wavefunction from scratch for each new system, thus requiring long optimization. In this work, we propose a novel neural network ansatz, which effectively maps uncorrelated, computationally cheap Hartree-Fock orbitals, to correlated, high-accuracy neural network orbitals. This ansatz is inherently capable of learning a single wavefunction across multiple compounds and geometries, as we demonstrate by successfully transferring a wavefunction model pre-trained on smaller fragments to larger compounds. Furthermore, we provide ample experimental evidence to support the idea that extensive pre-training of a such a generalized wavefunction model across different compounds and geometries could lead to a foundation wavefunction model. Such a model could yield high-accuracy ab-initio energies using only minimal computational effort for fine-tuning and evaluation of observables.

Gold-standard solutions to the Schrödinger equation using deep learning: How much physics do we need?

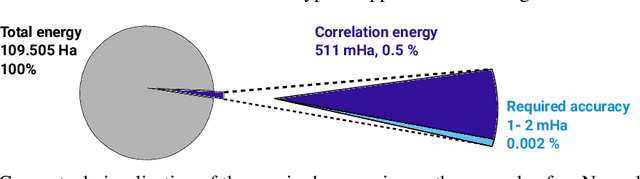
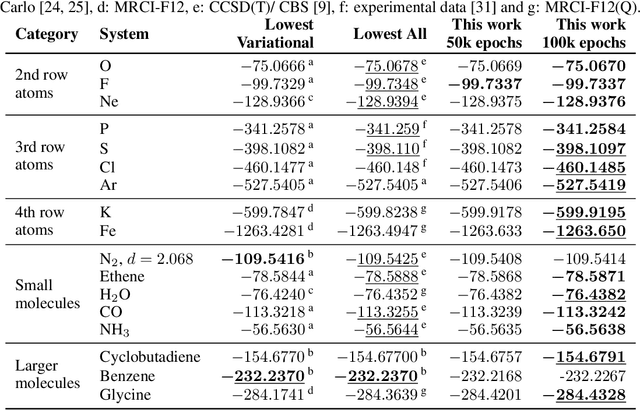
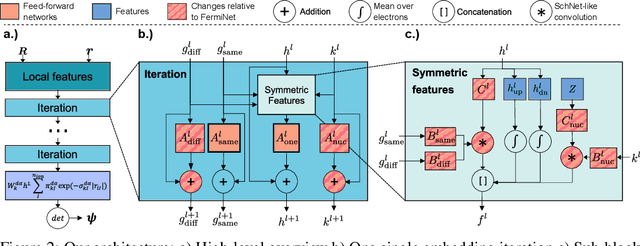
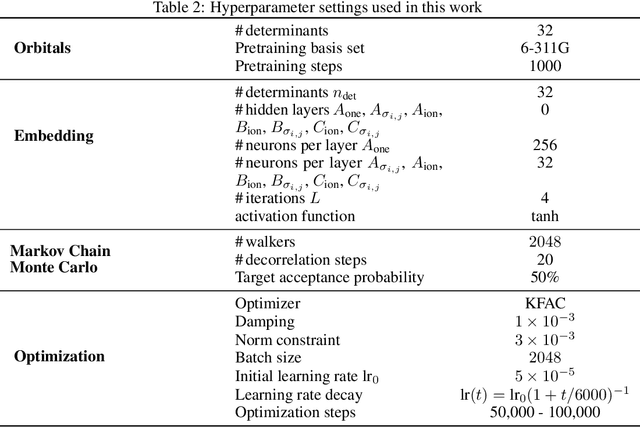
Finding accurate solutions to the Schr\"odinger equation is the key unsolved challenge of computational chemistry. Given its importance for the development of new chemical compounds, decades of research have been dedicated to this problem, but due to the large dimensionality even the best available methods do not yet reach the desired accuracy. Recently the combination of deep learning with Monte Carlo methods has emerged as a promising way to obtain highly accurate energies and moderate scaling of computational cost. In this paper we significantly contribute towards this goal by introducing a novel deep-learning architecture that achieves 40-70% lower energy error at 8x lower computational cost compared to previous approaches. Using our method we establish a new benchmark by calculating the most accurate variational ground state energies ever published for a number of different atoms and molecules. We systematically break down and measure our improvements, focusing in particular on the effect of increasing physical prior knowledge. We surprisingly find that increasing the prior knowledge given to the architecture can actually decrease accuracy.

Training ReLU networks to high uniform accuracy is intractable

Statistical learning theory provides bounds on the necessary number of training samples needed to reach a prescribed accuracy in a learning problem formulated over a given target class. This accuracy is typically measured in terms of a generalization error, that is, an expected value of a given loss function. However, for several applications -- for example in a security-critical context or for problems in the computational sciences -- accuracy in this sense is not sufficient. In such cases, one would like to have guarantees for high accuracy on every input value, that is, with respect to the uniform norm. In this paper we precisely quantify the number of training samples needed for any conceivable training algorithm to guarantee a given uniform accuracy on any learning problem formulated over target classes containing (or consisting of) ReLU neural networks of a prescribed architecture. We prove that, under very general assumptions, the minimal number of training samples for this task scales exponentially both in the depth and the input dimension of the network architecture. As a corollary we conclude that the training of ReLU neural networks to high uniform accuracy is intractable. In a security-critical context this points to the fact that deep learning based systems are prone to being fooled by a possible adversary. We corroborate our theoretical findings by numerical results.

Integral representations of shallow neural network with Rectified Power Unit activation function

In this effort, we derive a formula for the integral representation of a shallow neural network with the Rectified Power Unit activation function. Mainly, our first result deals with the univariate case of representation capability of RePU shallow networks. The multidimensional result in this paper characterizes the set of functions that can be represented with bounded norm and possibly unbounded width.

Sobolev-type embeddings for neural network approximation spaces

We consider neural network approximation spaces that classify functions according to the rate at which they can be approximated (with error measured in $L^p$) by ReLU neural networks with an increasing number of coefficients, subject to bounds on the magnitude of the coefficients and the number of hidden layers. We prove embedding theorems between these spaces for different values of $p$. Furthermore, we derive sharp embeddings of these approximation spaces into H\"older spaces. We find that, analogous to the case of classical function spaces (such as Sobolev spaces, or Besov spaces) it is possible to trade "smoothness" (i.e., approximation rate) for increased integrability. Combined with our earlier results in [arXiv:2104.02746], our embedding theorems imply a somewhat surprising fact related to "learning" functions from a given neural network space based on point samples: if accuracy is measured with respect to the uniform norm, then an optimal "learning" algorithm for reconstructing functions that are well approximable by ReLU neural networks is simply given by piecewise constant interpolation on a tensor product grid.