Gold-standard solutions to the Schrödinger equation using deep learning: How much physics do we need?

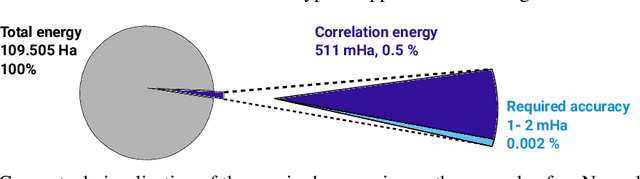
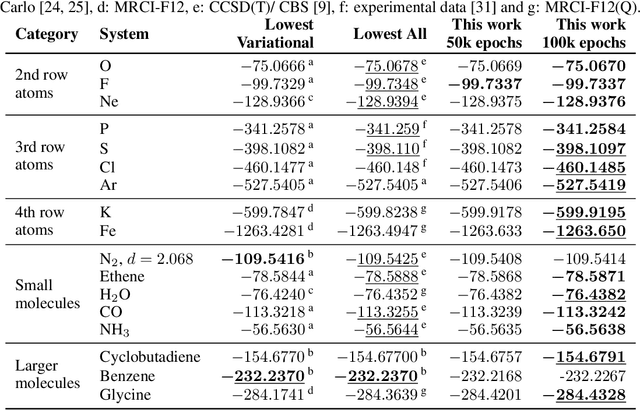
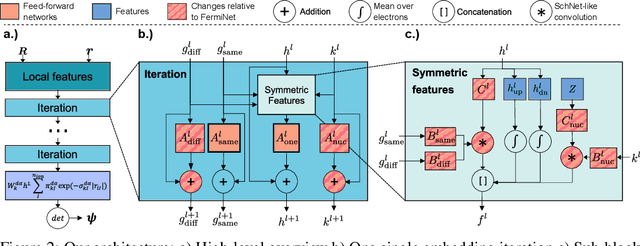
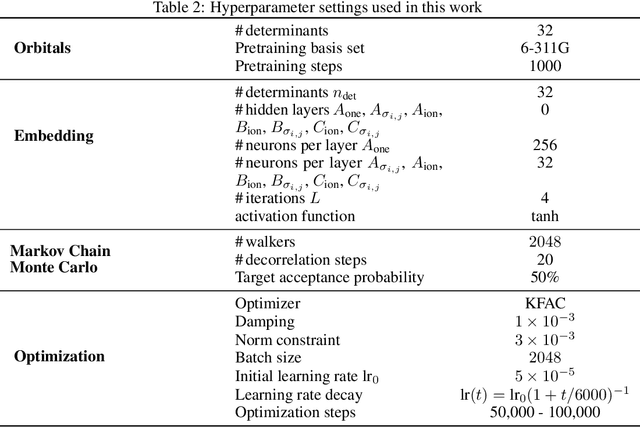
Finding accurate solutions to the Schr\"odinger equation is the key unsolved challenge of computational chemistry. Given its importance for the development of new chemical compounds, decades of research have been dedicated to this problem, but due to the large dimensionality even the best available methods do not yet reach the desired accuracy. Recently the combination of deep learning with Monte Carlo methods has emerged as a promising way to obtain highly accurate energies and moderate scaling of computational cost. In this paper we significantly contribute towards this goal by introducing a novel deep-learning architecture that achieves 40-70% lower energy error at 8x lower computational cost compared to previous approaches. Using our method we establish a new benchmark by calculating the most accurate variational ground state energies ever published for a number of different atoms and molecules. We systematically break down and measure our improvements, focusing in particular on the effect of increasing physical prior knowledge. We surprisingly find that increasing the prior knowledge given to the architecture can actually decrease accuracy.

Solving the electronic Schrödinger equation for multiple nuclear geometries with weight-sharing deep neural networks

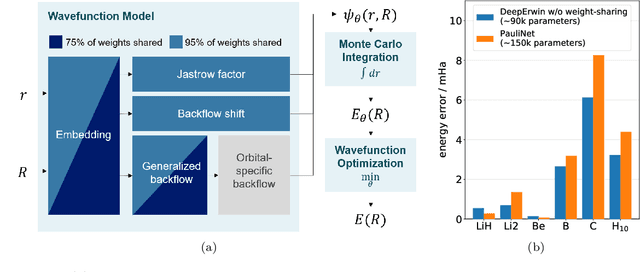
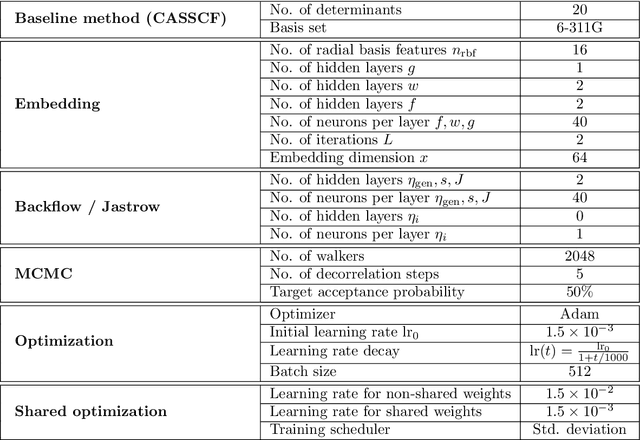
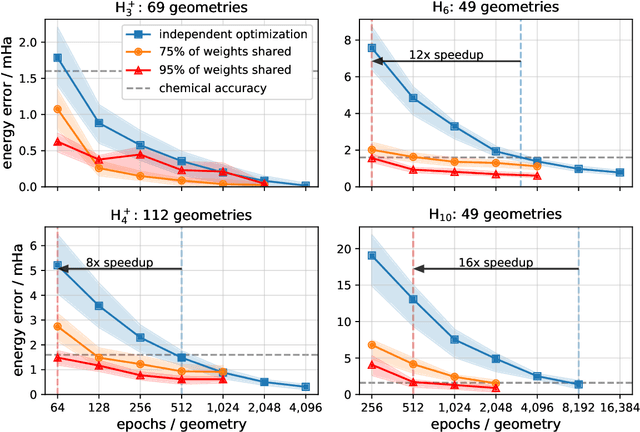
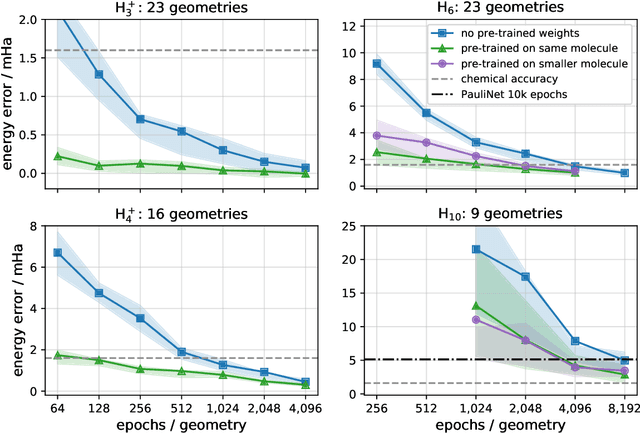
Accurate numerical solutions for the Schr\"odinger equation are of utmost importance in quantum chemistry. However, the computational cost of current high-accuracy methods scales poorly with the number of interacting particles. Combining Monte Carlo methods with unsupervised training of neural networks has recently been proposed as a promising approach to overcome the curse of dimensionality in this setting and to obtain accurate wavefunctions for individual molecules at a moderately scaling computational cost. These methods currently do not exploit the regularity exhibited by wavefunctions with respect to their molecular geometries. Inspired by recent successful applications of deep transfer learning in machine translation and computer vision tasks, we attempt to leverage this regularity by introducing a weight-sharing constraint when optimizing neural network-based models for different molecular geometries. That is, we restrict the optimization process such that up to 95 percent of weights in a neural network model are in fact equal across varying molecular geometries. We find that this technique can accelerate optimization when considering sets of nuclear geometries of the same molecule by an order of magnitude and that it opens a promising route towards pre-trained neural network wavefunctions that yield high accuracy even across different molecules.

Deep Learning for UV Absorption Spectra with SchNarc: First Steps Towards Transferability in Chemical Compound Space

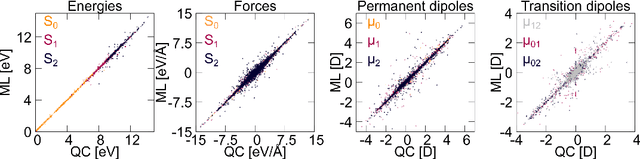
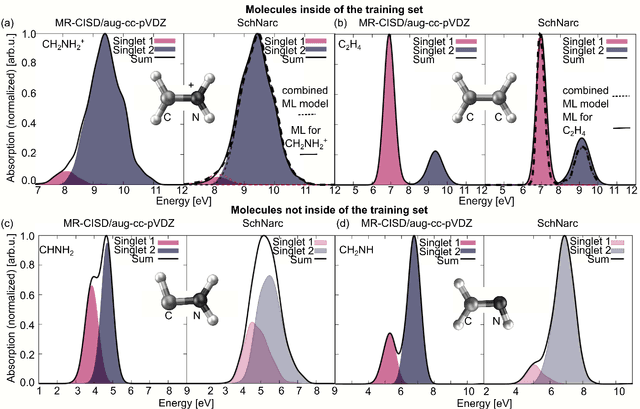
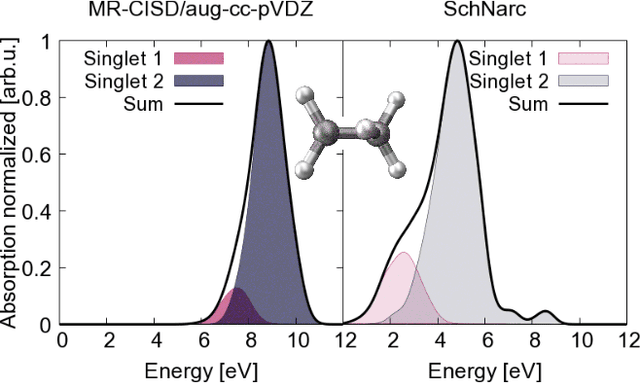
Machine learning (ML) has shown to advance the research field of quantum chemistry in almost any possible direction and has recently also entered the excited states to investigate the multifaceted photochemistry of molecules. In this paper, we pursue two goals: i) We show how ML can be used to model permanent dipole moments for excited states and transition dipole moments by adapting the charge model of [Chem. Sci., 2017, 8, 6924-6935], which was originally proposed for the permanent dipole moment vector of the electronic ground state. ii) We investigate the transferability of our excited-state ML models in chemical space, i.e., whether an ML model can predict properties of molecules that it has never been trained on and whether it can learn the different excited states of two molecules simultaneously. To this aim, we employ and extend our previously reported SchNarc approach for excited-state ML. We calculate UV absorption spectra from excited-state energies and transition dipole moments as well as electrostatic potentials from latent charges inferred by the ML model of the permanent dipole moment vectors. We train our ML models on CH$_2$NH$_2^+$ and C$_2$H$_4$, while predictions are carried out for these molecules and additionally for CHNH$_2$, CH$_2$NH, and C$_2$H$_5^+$. The results indicate that transferability is possible for the excited states.

Machine learning for electronically excited states of molecules

Electronically excited states of molecules are at the heart of photochemistry, photophysics, as well as photobiology and also play a role in material science. Their theoretical description requires highly accurate quantum chemical calculations, which are computationally expensive. In this review, we focus on how machine learning is employed not only to speed up such excited-state simulations but also how this branch of artificial intelligence can be used to advance this exciting research field in all its aspects. Discussed applications of machine learning for excited states include excited-state dynamics simulations, static calculations of absorption spectra, as well as many others. In order to put these studies into context, we discuss the promises and pitfalls of the involved machine learning techniques. Since the latter are mostly based on quantum chemistry calculations, we also provide a short introduction into excited-state electronic structure methods, approaches for nonadiabatic dynamics simulations and describe tricks and problems when using them in machine learning for excited states of molecules.

Machine learning and excited-state molecular dynamics

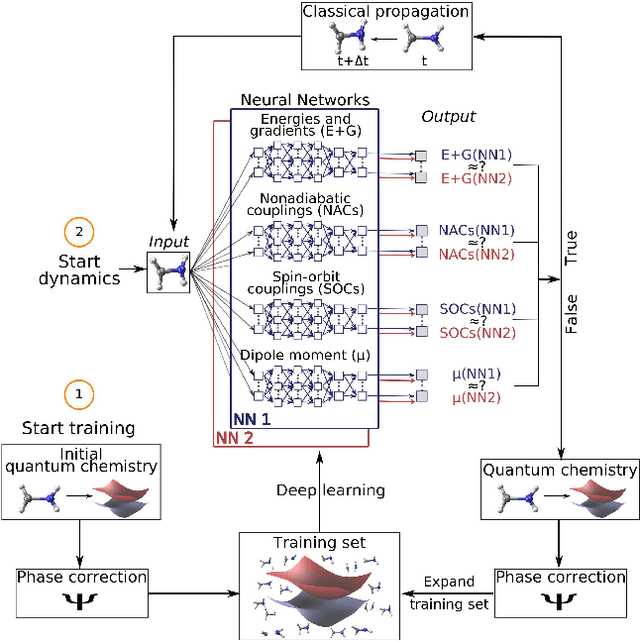
Machine learning is employed at an increasing rate in the research field of quantum chemistry. While the majority of approaches target the investigation of chemical systems in their electronic ground state, the inclusion of light into the processes leads to electronically excited states and gives rise to several new challenges. Here, we survey recent advances for excited-state dynamics based on machine learning. In doing so, we highlight successes, pitfalls, challenges and future avenues for machine learning approaches for light-induced molecular processes.

Combining SchNet and SHARC: The SchNarc machine learning approach for excited-state dynamics

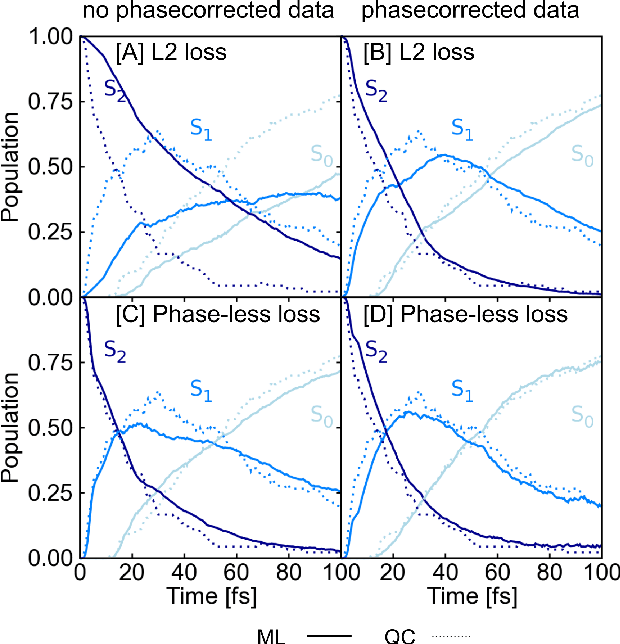
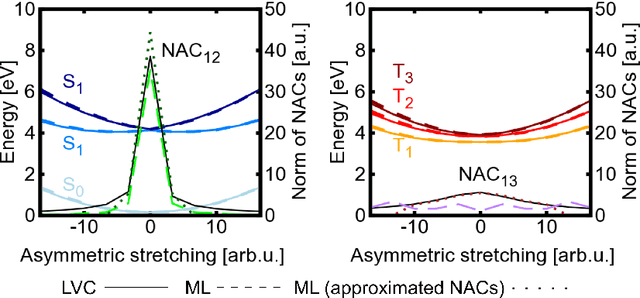
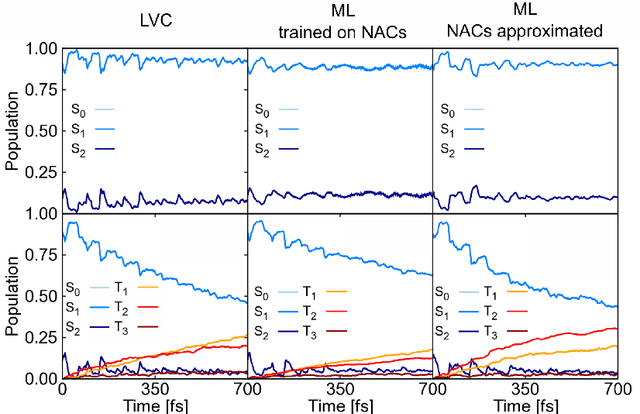
In recent years, deep learning has become a part of our everyday life and is revolutionizing quantum chemistry as well. In this work, we show how deep learning can be used to advance the research field of photochemistry by learning all important properties for photodynamics simulations. The properties are multiple energies, forces, nonadiabatic couplings and spin-orbit couplings. The nonadiabatic couplings are learned in a phase-free manner as derivatives of a virtually constructed property by the deep learning model, which guarantees rotational covariance. Additionally, an approximation for nonadiabatic couplings is introduced, based on the potentials, their gradients and Hessians. As deep-learning method, we employ SchNet extended for multiple electronic states. In combination with the molecular dynamics program SHARC, our approach termed SchNarc is tested on a model system and two realistic polyatomic molecules and paves the way towards efficient photodynamics simulations of complex systems.

Neural networks and kernel ridge regression for excited states dynamics of CH$_2$NH$_2^+$: From single-state to multi-state representations and multi-property machine learning models

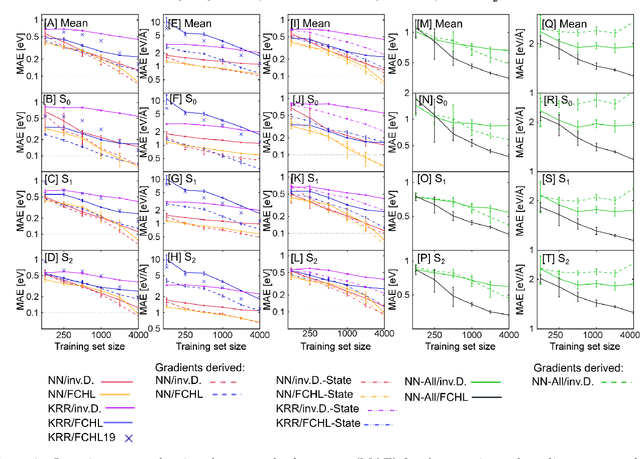
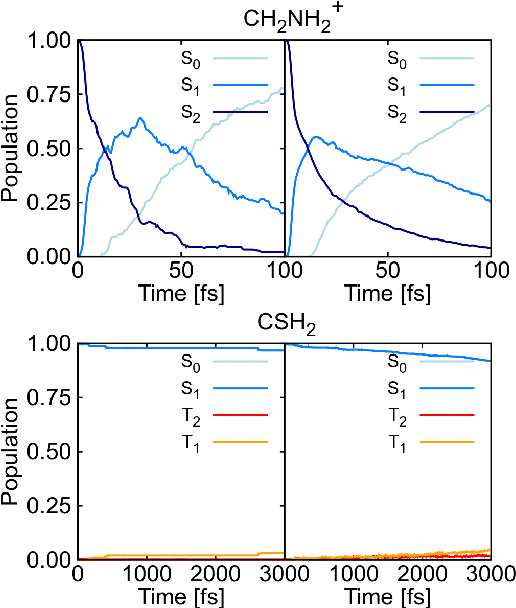
Excited-state dynamics simulations are a powerful tool to investigate photo-induced reactions of molecules and materials and provide complementary information to experiments. Since the applicability of these simulation techniques is limited by the costs of the underlying electronic structure calculations, we develop and assess different machine learning models for this task. The machine learning models are trained on {\emph ab initio} calculations for excited electronic states, using the methylenimmonium cation (CH$_2$NH$_2^+$) as a model system. For the prediction of excited-state properties, multiple outputs are desirable, which is straightforward with neural networks but less explored with kernel ridge regression. We overcome this challenge for kernel ridge regression in the case of energy predictions by encoding the electronic states explicitly in the inputs, in addition to the molecular representation. We adopt this strategy also for our neural networks for comparison. Such a state encoding enables not only kernel ridge regression with multiple outputs but leads also to more accurate machine learning models for state-specific properties. An important goal for excited-state machine learning models is their use in dynamics simulations, which needs not only state-specific information but also couplings, i.e., properties involving pairs of states. Accordingly, we investigate the performance of different models for such coupling elements. Furthermore, we explore how combining all properties in a single neural network affects the accuracy. As an ultimate test for our machine learning models, we carry out excited-state dynamics simulations based on the predicted energies, forces and couplings and, thus, show the scopes and possibilities of machine learning for the treatment of electronically excited states.

Molecular Dynamics with Neural-Network Potentials

Molecular dynamics simulations are an important tool for describing the evolution of a chemical system with time. However, these simulations are inherently held back either by the prohibitive cost of accurate electronic structure theory computations or the limited accuracy of classical empirical force fields. Machine learning techniques can help to overcome these limitations by providing access to potential energies, forces and other molecular properties modeled directly after an electronic structure reference at only a fraction of the original computational cost. The present text discusses several practical aspects of conducting machine learning driven molecular dynamics simulations. First, we study the efficient selection of reference data points on the basis of an active learning inspired adaptive sampling scheme. This is followed by the analysis of a machine-learning based model for simulating molecular dipole moments in the framework of predicting infrared spectra via molecular dynamics simulations. Finally, we show that machine learning models can offer valuable aid in understanding chemical systems beyond a simple prediction of quantities.

Machine learning enables long time scale molecular photodynamics simulations

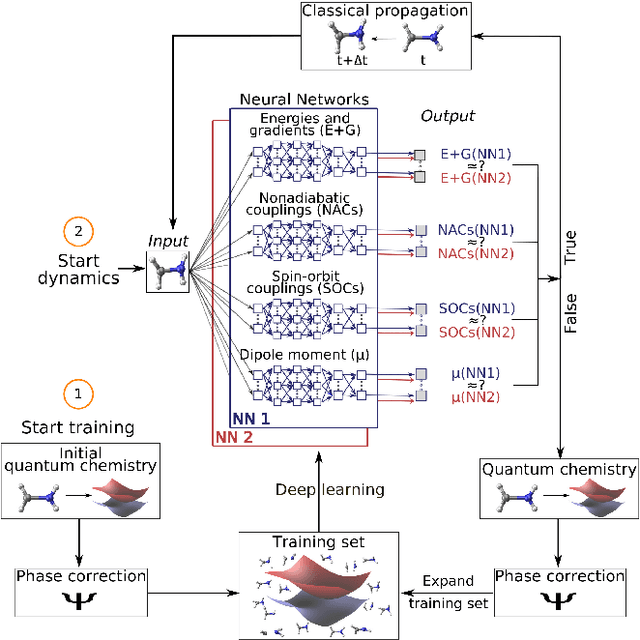
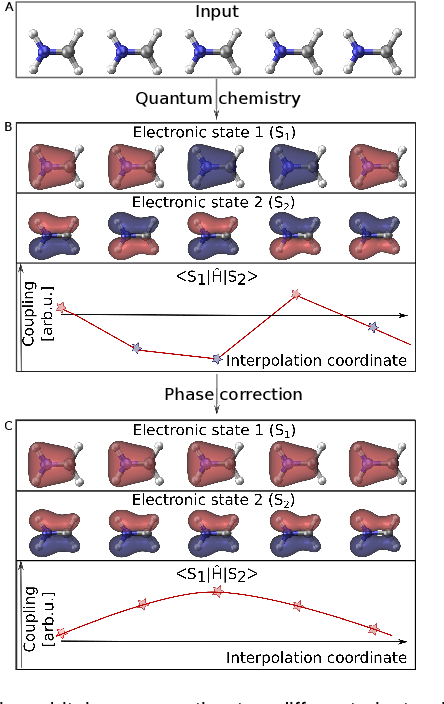
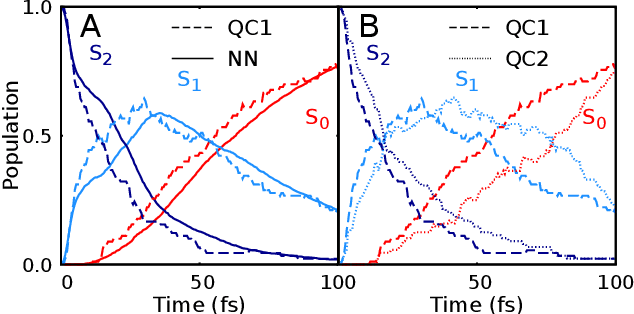
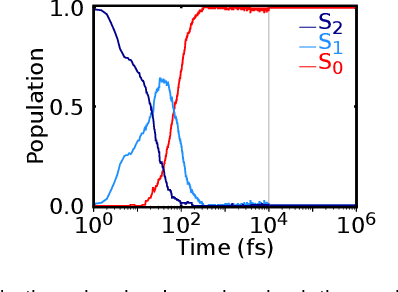
Photo-induced processes are fundamental in nature, but accurate simulations are seriously limited by the cost of the underlying quantum chemical calculations, hampering their application for long time scales. Here we introduce a method based on machine learning to overcome this bottleneck and enable accurate photodynamics on nanosecond time scales, which are otherwise out of reach with contemporary approaches. Instead of expensive quantum chemistry during molecular dynamics simulations, we use deep neural networks to learn the relationship between a molecular geometry and its high-dimensional electronic properties. As an example, the time evolution of the methylenimmonium cation for one nanosecond is used to demonstrate that machine learning algorithms can outperform standard excited-state molecular dynamics approaches in their computational efficiency while delivering the same accuracy.