Leon Gerard
Transferable Neural Wavefunctions for Solids
May 13, 2024



Abstract:Deep-Learning-based Variational Monte Carlo (DL-VMC) has recently emerged as a highly accurate approach for finding approximate solutions to the many-electron Schr\"odinger equation. Despite its favorable scaling with the number of electrons, $\mathcal{O}(n_\text{el}^{4})$, the practical value of DL-VMC is limited by the high cost of optimizing the neural network weights for every system studied. To mitigate this problem, recent research has proposed optimizing a single neural network across multiple systems, reducing the cost per system. Here we extend this approach to solids, where similar but distinct calculations using different geometries, boundary conditions, and supercell sizes are often required. We show how to optimize a single ansatz across all of these variations, reducing the required number of optimization steps by an order of magnitude. Furthermore, we exploit the transfer capabilities of a pre-trained network. We successfully transfer a network, pre-trained on 2x2x2 supercells of LiH, to 3x3x3 supercells. This reduces the number of optimization steps required to simulate the large system by a factor of 50 compared to previous work.
Variational Monte Carlo on a Budget -- Fine-tuning pre-trained Neural Wavefunctions
Jul 15, 2023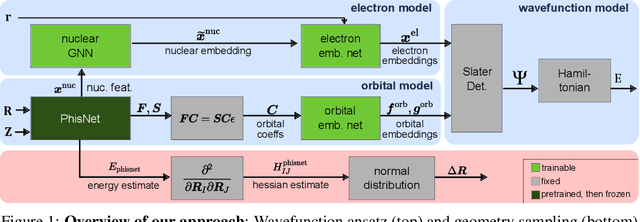
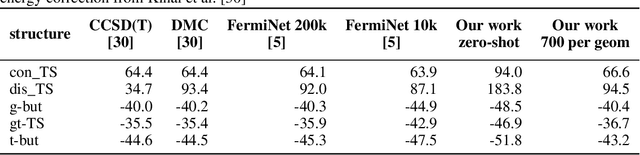
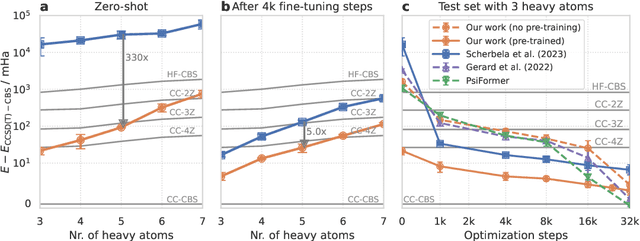
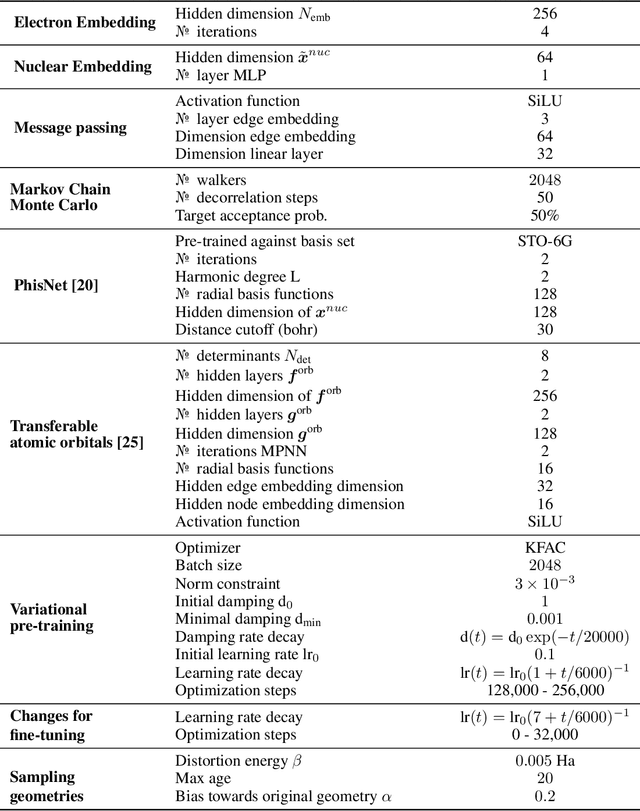
Abstract:Obtaining accurate solutions to the Schr\"odinger equation is the key challenge in computational quantum chemistry. Deep-learning-based Variational Monte Carlo (DL-VMC) has recently outperformed conventional approaches in terms of accuracy, but only at large computational cost. Whereas in many domains models are trained once and subsequently applied for inference, accurate DL-VMC so far requires a full optimization for every new problem instance, consuming thousands of GPUhs even for small molecules. We instead propose a DL-VMC model which has been pre-trained using self-supervised wavefunction optimization on a large and chemically diverse set of molecules. Applying this model to new molecules without any optimization, yields wavefunctions and absolute energies that outperform established methods such as CCSD(T)-2Z. To obtain accurate relative energies, only few fine-tuning steps of this base model are required. We accomplish this with a fully end-to-end machine-learned model, consisting of an improved geometry embedding architecture and an existing SE(3)-equivariant model to represent molecular orbitals. Combining this architecture with continuous sampling of geometries, we improve zero-shot accuracy by two orders of magnitude compared to the state of the art. We extensively evaluate the accuracy, scalability and limitations of our base model on a wide variety of test systems.
Towards a Foundation Model for Neural Network Wavefunctions
Mar 17, 2023Abstract:Deep neural networks have become a highly accurate and powerful wavefunction ansatz in combination with variational Monte Carlo methods for solving the electronic Schr\"odinger equation. However, despite their success and favorable scaling, these methods are still computationally too costly for wide adoption. A significant obstacle is the requirement to optimize the wavefunction from scratch for each new system, thus requiring long optimization. In this work, we propose a novel neural network ansatz, which effectively maps uncorrelated, computationally cheap Hartree-Fock orbitals, to correlated, high-accuracy neural network orbitals. This ansatz is inherently capable of learning a single wavefunction across multiple compounds and geometries, as we demonstrate by successfully transferring a wavefunction model pre-trained on smaller fragments to larger compounds. Furthermore, we provide ample experimental evidence to support the idea that extensive pre-training of a such a generalized wavefunction model across different compounds and geometries could lead to a foundation wavefunction model. Such a model could yield high-accuracy ab-initio energies using only minimal computational effort for fine-tuning and evaluation of observables.
Gold-standard solutions to the Schrödinger equation using deep learning: How much physics do we need?
May 31, 2022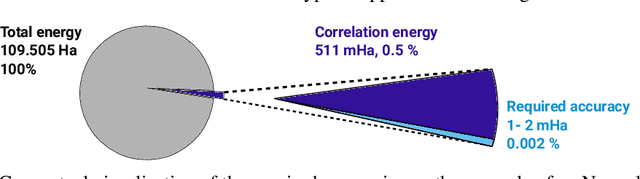
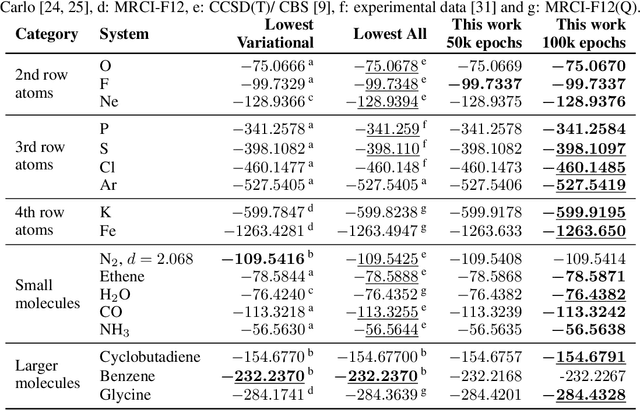
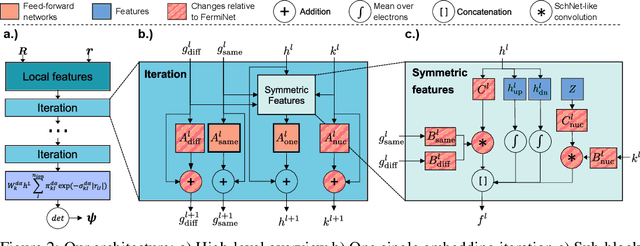
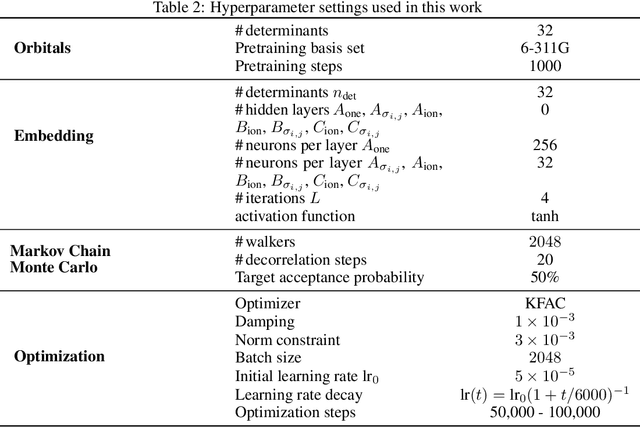
Abstract:Finding accurate solutions to the Schr\"odinger equation is the key unsolved challenge of computational chemistry. Given its importance for the development of new chemical compounds, decades of research have been dedicated to this problem, but due to the large dimensionality even the best available methods do not yet reach the desired accuracy. Recently the combination of deep learning with Monte Carlo methods has emerged as a promising way to obtain highly accurate energies and moderate scaling of computational cost. In this paper we significantly contribute towards this goal by introducing a novel deep-learning architecture that achieves 40-70% lower energy error at 8x lower computational cost compared to previous approaches. Using our method we establish a new benchmark by calculating the most accurate variational ground state energies ever published for a number of different atoms and molecules. We systematically break down and measure our improvements, focusing in particular on the effect of increasing physical prior knowledge. We surprisingly find that increasing the prior knowledge given to the architecture can actually decrease accuracy.
Solving the electronic Schrödinger equation for multiple nuclear geometries with weight-sharing deep neural networks
May 18, 2021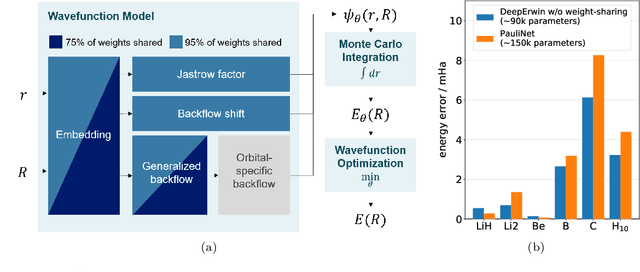
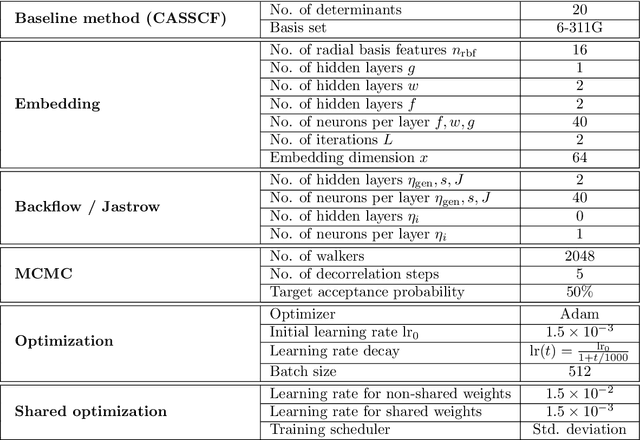
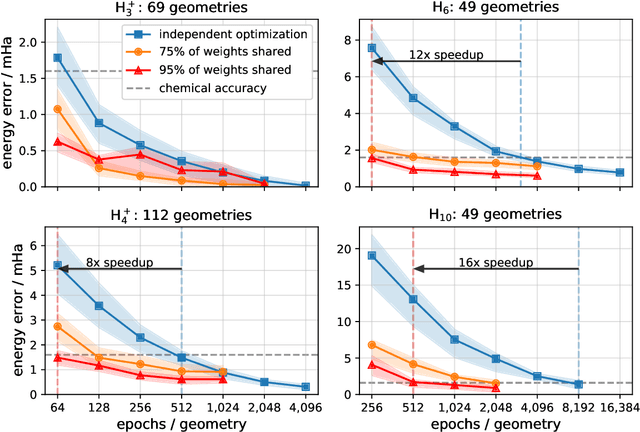
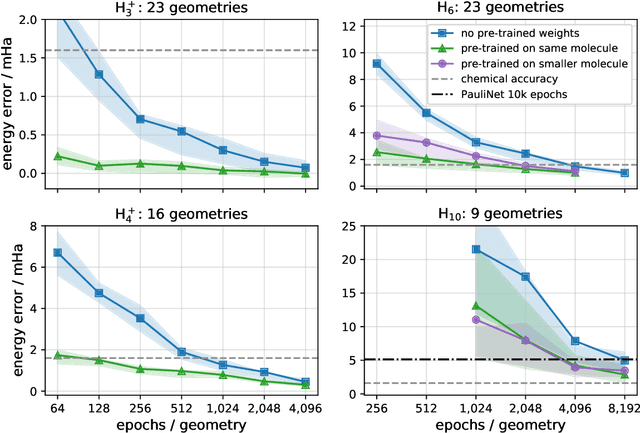
Abstract:Accurate numerical solutions for the Schr\"odinger equation are of utmost importance in quantum chemistry. However, the computational cost of current high-accuracy methods scales poorly with the number of interacting particles. Combining Monte Carlo methods with unsupervised training of neural networks has recently been proposed as a promising approach to overcome the curse of dimensionality in this setting and to obtain accurate wavefunctions for individual molecules at a moderately scaling computational cost. These methods currently do not exploit the regularity exhibited by wavefunctions with respect to their molecular geometries. Inspired by recent successful applications of deep transfer learning in machine translation and computer vision tasks, we attempt to leverage this regularity by introducing a weight-sharing constraint when optimizing neural network-based models for different molecular geometries. That is, we restrict the optimization process such that up to 95 percent of weights in a neural network model are in fact equal across varying molecular geometries. We find that this technique can accelerate optimization when considering sets of nuclear geometries of the same molecule by an order of magnitude and that it opens a promising route towards pre-trained neural network wavefunctions that yield high accuracy even across different molecules.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge