Enhanced sampling of robust molecular datasets with uncertainty-based collective variables

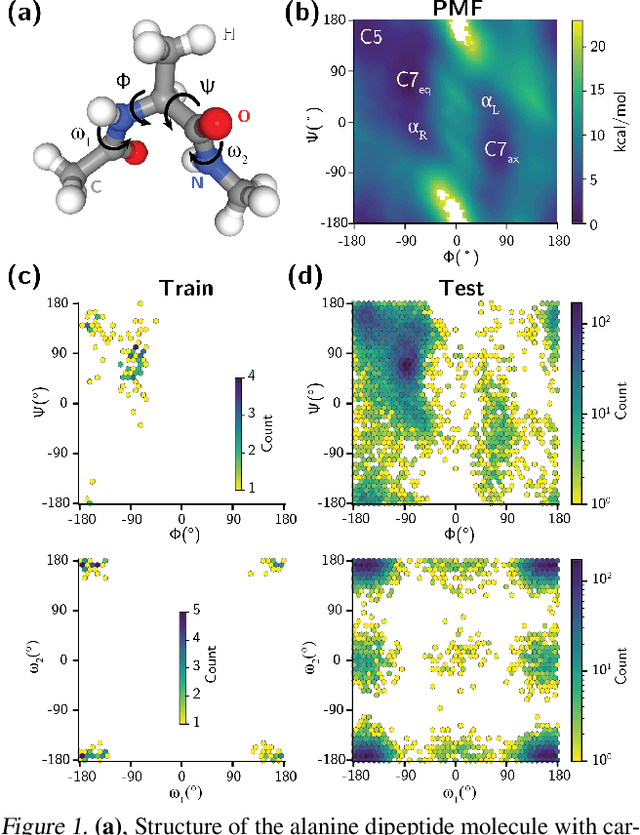
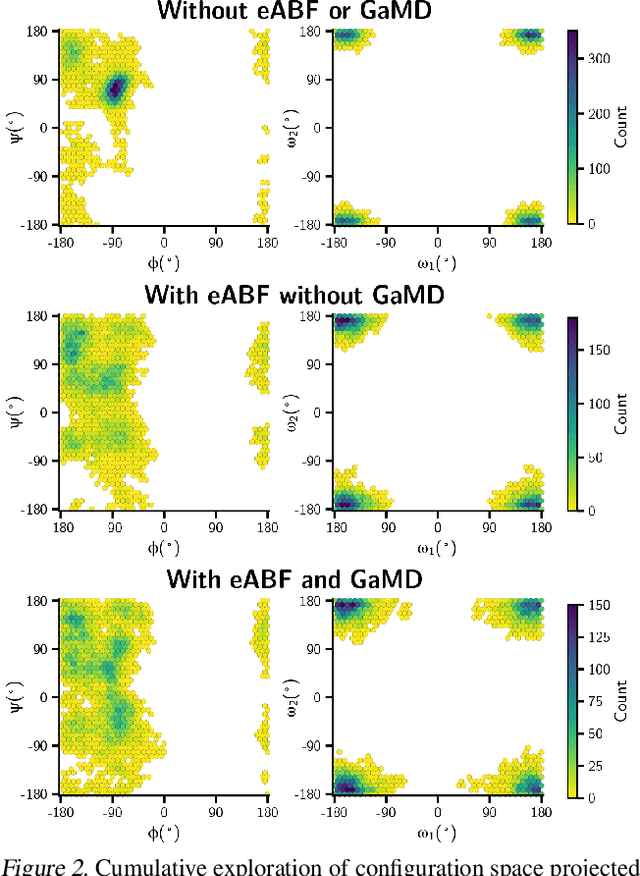
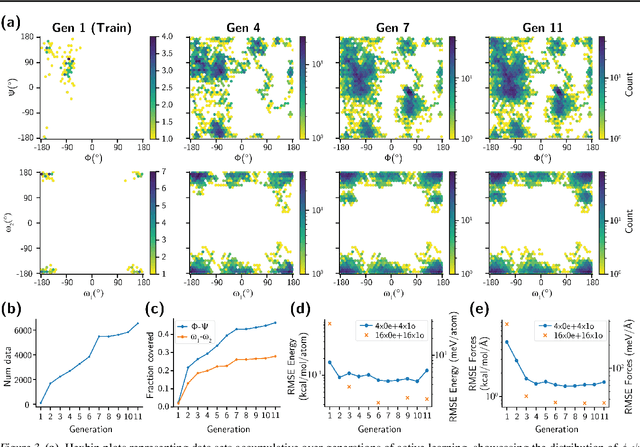
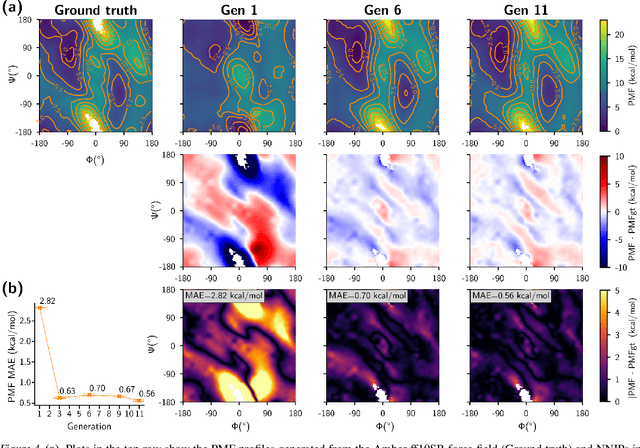
Generating a data set that is representative of the accessible configuration space of a molecular system is crucial for the robustness of machine learned interatomic potentials (MLIP). However, the complexity of molecular systems, characterized by intricate potential energy surfaces (PESs) with numerous local minima and energy barriers, presents a significant challenge. Traditional methods of data generation, such as random sampling or exhaustive exploration, are either intractable or may not capture rare, but highly informative configurations. In this study, we propose a method that leverages uncertainty as the collective variable (CV) to guide the acquisition of chemically-relevant data points, focusing on regions of the configuration space where ML model predictions are most uncertain. This approach employs a Gaussian Mixture Model-based uncertainty metric from a single model as the CV for biased molecular dynamics simulations. The effectiveness of our approach in overcoming energy barriers and exploring unseen energy minima, thereby enhancing the data set in an active learning framework, is demonstrated on the alanine dipeptide benchmark system.

Learning Collective Variables for Protein Folding with Labeled Data Augmentation through Geodesic Interpolation

In molecular dynamics (MD) simulations, rare events, such as protein folding, are typically studied by means of enhanced sampling techniques, most of which rely on the definition of a collective variable (CV) along which the acceleration occurs. Obtaining an expressive CV is crucial, but often hindered by the lack of information about the particular event, e.g., the transition from unfolded to folded conformation. We propose a simulation-free data augmentation strategy using physics-inspired metrics to generate geodesic interpolations resembling protein folding transitions, thereby improving sampling efficiency without true transition state samples. Leveraging interpolation progress parameters, we introduce a regression-based learning scheme for CV models, which outperforms classifier-based methods when transition state data is limited and noisy

Single-model uncertainty quantification in neural network potentials does not consistently outperform model ensembles

Neural networks (NNs) often assign high confidence to their predictions, even for points far out-of-distribution, making uncertainty quantification (UQ) a challenge. When they are employed to model interatomic potentials in materials systems, this problem leads to unphysical structures that disrupt simulations, or to biased statistics and dynamics that do not reflect the true physics. Differentiable UQ techniques can find new informative data and drive active learning loops for robust potentials. However, a variety of UQ techniques, including newly developed ones, exist for atomistic simulations and there are no clear guidelines for which are most effective or suitable for a given case. In this work, we examine multiple UQ schemes for improving the robustness of NN interatomic potentials (NNIPs) through active learning. In particular, we compare incumbent ensemble-based methods against strategies that use single, deterministic NNs: mean-variance estimation, deep evidential regression, and Gaussian mixture models. We explore three datasets ranging from in-domain interpolative learning to more extrapolative out-of-domain generalization challenges: rMD17, ammonia inversion, and bulk silica glass. Performance is measured across multiple metrics relating model error to uncertainty. Our experiments show that none of the methods consistently outperformed each other across the various metrics. Ensembling remained better at generalization and for NNIP robustness; MVE only proved effective for in-domain interpolation, while GMM was better out-of-domain; and evidential regression, despite its promise, was not the preferable alternative in any of the cases. More broadly, cost-effective, single deterministic models cannot yet consistently match or outperform ensembling for uncertainty quantification in NNIPs.

Differentiable Simulations for Enhanced Sampling of Rare Events

We develop a novel approach to enhanced sampling of chemically reactive events using differentiable simulations. We merge the reaction path discovery and biasing potential computation into one end-to-end problem and solve it by path-integral optimization. The techniques developed contribute directly to the understanding and usability of differentiable simulations as we introduce new approaches and prove the stability properties of our method.