On best approximation by multivariate ridge functions with applications to generalized translation networks

We prove sharp upper and lower bounds for the approximation of Sobolev functions by sums of multivariate ridge functions, i.e., functions of the form $\mathbb{R}^d \ni x \mapsto \sum_{k=1}^n h_k(A_k x) \in \mathbb{R}$ with $h_k : \mathbb{R}^\ell \to \mathbb{R}$ and $A_k \in \mathbb{R}^{\ell \times d}$. We show that the order of approximation asymptotically behaves as $n^{-r/(d-\ell)}$, where $r$ is the regularity of the Sobolev functions to be approximated. Our lower bound even holds when approximating $L^\infty$-Sobolev functions of regularity $r$ with error measured in $L^1$, while our upper bound applies to the approximation of $L^p$-Sobolev functions in $L^p$ for any $1 \leq p \leq \infty$. These bounds generalize well-known results about the approximation properties of univariate ridge functions to the multivariate case. Moreover, we use these bounds to obtain sharp asymptotic bounds for the approximation of Sobolev functions using generalized translation networks and complex-valued neural networks.

On the Lipschitz constant of random neural networks

Empirical studies have widely demonstrated that neural networks are highly sensitive to small, adversarial perturbations of the input. The worst-case robustness against these so-called adversarial examples can be quantified by the Lipschitz constant of the neural network. However, only few theoretical results regarding this quantity exist in the literature. In this paper, we initiate the study of the Lipschitz constant of random ReLU neural networks, i.e., neural networks whose weights are chosen at random and which employ the ReLU activation function. For shallow neural networks, we characterize the Lipschitz constant up to an absolute numerical constant. Moreover, we extend our analysis to deep neural networks of sufficiently large width where we prove upper and lower bounds for the Lipschitz constant. These bounds match up to a logarithmic factor that depends on the depth.

Optimal approximation of $C^k$-functions using shallow complex-valued neural networks

We prove a quantitative result for the approximation of functions of regularity $C^k$ (in the sense of real variables) defined on the complex cube $\Omega_n := [-1,1]^n +i[-1,1]^n\subseteq \mathbb{C}^n$ using shallow complex-valued neural networks. Precisely, we consider neural networks with a single hidden layer and $m$ neurons, i.e., networks of the form $z \mapsto \sum_{j=1}^m \sigma_j \cdot \phi\big(\rho_j^T z + b_j\big)$ and show that one can approximate every function in $C^k \left( \Omega_n; \mathbb{C}\right)$ using a function of that form with error of the order $m^{-k/(2n)}$ as $m \to \infty$, provided that the activation function $\phi: \mathbb{C} \to \mathbb{C}$ is smooth but not polyharmonic on some non-empty open set. Furthermore, we show that the selection of the weights $\sigma_j, b_j \in \mathbb{C}$ and $\rho_j \in \mathbb{C}^n$ is continuous with respect to $f$ and prove that the derived rate of approximation is optimal under this continuity assumption. We also discuss the optimality of the result for a possibly discontinuous choice of the weights.

$L^p$ sampling numbers for the Fourier-analytic Barron space

In this paper, we consider Barron functions $f : [0,1]^d \to \mathbb{R}$ of smoothness $\sigma > 0$, which are functions that can be written as \[ f(x) = \int_{\mathbb{R}^d} F(\xi) \, e^{2 \pi i \langle x, \xi \rangle} \, d \xi \quad \text{with} \quad \int_{\mathbb{R}^d} |F(\xi)| \cdot (1 + |\xi|)^{\sigma} \, d \xi < \infty. \] For $\sigma = 1$, these functions play a prominent role in machine learning, since they can be efficiently approximated by (shallow) neural networks without suffering from the curse of dimensionality. For these functions, we study the following question: Given $m$ point samples $f(x_1),\dots,f(x_m)$ of an unknown Barron function $f : [0,1]^d \to \mathbb{R}$ of smoothness $\sigma$, how well can $f$ be recovered from these samples, for an optimal choice of the sampling points and the reconstruction procedure? Denoting the optimal reconstruction error measured in $L^p$ by $s_m (\sigma; L^p)$, we show that \[ m^{- \frac{1}{\max \{ p,2 \}} - \frac{\sigma}{d}} \lesssim s_m(\sigma;L^p) \lesssim (\ln (e + m))^{\alpha(\sigma,d) / p} \cdot m^{- \frac{1}{\max \{ p,2 \}} - \frac{\sigma}{d}} , \] where the implied constants only depend on $\sigma$ and $d$ and where $\alpha(\sigma,d)$ stays bounded as $d \to \infty$.

Training ReLU networks to high uniform accuracy is intractable

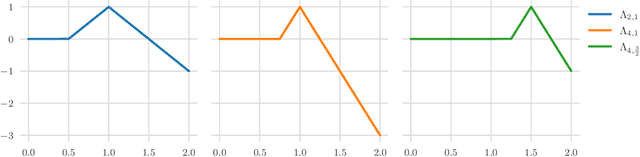
Statistical learning theory provides bounds on the necessary number of training samples needed to reach a prescribed accuracy in a learning problem formulated over a given target class. This accuracy is typically measured in terms of a generalization error, that is, an expected value of a given loss function. However, for several applications -- for example in a security-critical context or for problems in the computational sciences -- accuracy in this sense is not sufficient. In such cases, one would like to have guarantees for high accuracy on every input value, that is, with respect to the uniform norm. In this paper we precisely quantify the number of training samples needed for any conceivable training algorithm to guarantee a given uniform accuracy on any learning problem formulated over target classes containing (or consisting of) ReLU neural networks of a prescribed architecture. We prove that, under very general assumptions, the minimal number of training samples for this task scales exponentially both in the depth and the input dimension of the network architecture. As a corollary we conclude that the training of ReLU neural networks to high uniform accuracy is intractable. In a security-critical context this points to the fact that deep learning based systems are prone to being fooled by a possible adversary. We corroborate our theoretical findings by numerical results.

Optimal learning of high-dimensional classification problems using deep neural networks

We study the problem of learning classification functions from noiseless training samples, under the assumption that the decision boundary is of a certain regularity. We establish universal lower bounds for this estimation problem, for general classes of continuous decision boundaries. For the class of locally Barron-regular decision boundaries, we find that the optimal estimation rates are essentially independent of the underlying dimension and can be realized by empirical risk minimization methods over a suitable class of deep neural networks. These results are based on novel estimates of the $L^1$ and $L^\infty$ entropies of the class of Barron-regular functions.

Sobolev-type embeddings for neural network approximation spaces

We consider neural network approximation spaces that classify functions according to the rate at which they can be approximated (with error measured in $L^p$) by ReLU neural networks with an increasing number of coefficients, subject to bounds on the magnitude of the coefficients and the number of hidden layers. We prove embedding theorems between these spaces for different values of $p$. Furthermore, we derive sharp embeddings of these approximation spaces into H\"older spaces. We find that, analogous to the case of classical function spaces (such as Sobolev spaces, or Besov spaces) it is possible to trade "smoothness" (i.e., approximation rate) for increased integrability. Combined with our earlier results in [arXiv:2104.02746], our embedding theorems imply a somewhat surprising fact related to "learning" functions from a given neural network space based on point samples: if accuracy is measured with respect to the uniform norm, then an optimal "learning" algorithm for reconstructing functions that are well approximable by ReLU neural networks is simply given by piecewise constant interpolation on a tensor product grid.

Proof of the Theory-to-Practice Gap in Deep Learning via Sampling Complexity bounds for Neural Network Approximation Spaces

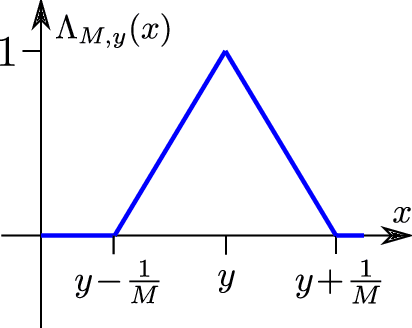
We study the computational complexity of (deterministic or randomized) algorithms based on point samples for approximating or integrating functions that can be well approximated by neural networks. Such algorithms (most prominently stochastic gradient descent and its variants) are used extensively in the field of deep learning. One of the most important problems in this field concerns the question of whether it is possible to realize theoretically provable neural network approximation rates by such algorithms. We answer this question in the negative by proving hardness results for the problems of approximation and integration on a novel class of neural network approximation spaces. In particular, our results confirm a conjectured and empirically observed theory-to-practice gap in deep learning. We complement our hardness results by showing that approximation rates of a comparable order of convergence are (at least theoretically) achievable.

The universal approximation theorem for complex-valued neural networks

We generalize the classical universal approximation theorem for neural networks to the case of complex-valued neural networks. Precisely, we consider feedforward networks with a complex activation function $\sigma : \mathbb{C} \to \mathbb{C}$ in which each neuron performs the operation $\mathbb{C}^N \to \mathbb{C}, z \mapsto \sigma(b + w^T z)$ with weights $w \in \mathbb{C}^N$ and a bias $b \in \mathbb{C}$, and with $\sigma$ applied componentwise. We completely characterize those activation functions $\sigma$ for which the associated complex networks have the universal approximation property, meaning that they can uniformly approximate any continuous function on any compact subset of $\mathbb{C}^d$ arbitrarily well. Unlike the classical case of real networks, the set of "good activation functions" which give rise to networks with the universal approximation property differs significantly depending on whether one considers deep networks or shallow networks: For deep networks with at least two hidden layers, the universal approximation property holds as long as $\sigma$ is neither a polynomial, a holomorphic function, or an antiholomorphic function. Shallow networks, on the other hand, are universal if and only if the real part or the imaginary part of $\sigma$ is not a polyharmonic function.

Neural network approximation and estimation of classifiers with classification boundary in a Barron class

We prove bounds for the approximation and estimation of certain classification functions using ReLU neural networks. Our estimation bounds provide a priori performance guarantees for empirical risk minimization using networks of a suitable size, depending on the number of training samples available. The obtained approximation and estimation rates are independent of the dimension of the input, showing that the curse of dimension can be overcome in this setting; in fact, the input dimension only enters in the form of a polynomial factor. Regarding the regularity of the target classification function, we assume the interfaces between the different classes to be locally of Barron-type. We complement our results by studying the relations between various Barron-type spaces that have been proposed in the literature. These spaces differ substantially more from each other than the current literature suggests.