Palina Salanevich
PtyGenography: using generative models for regularization of the phase retrieval problem
Feb 03, 2025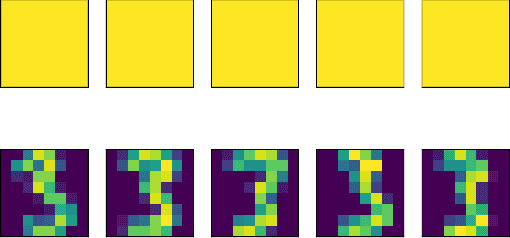
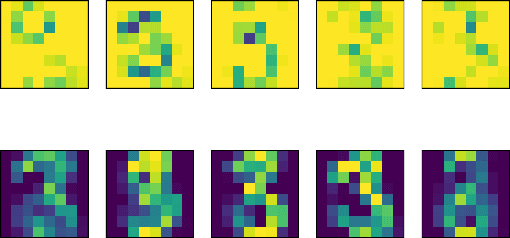
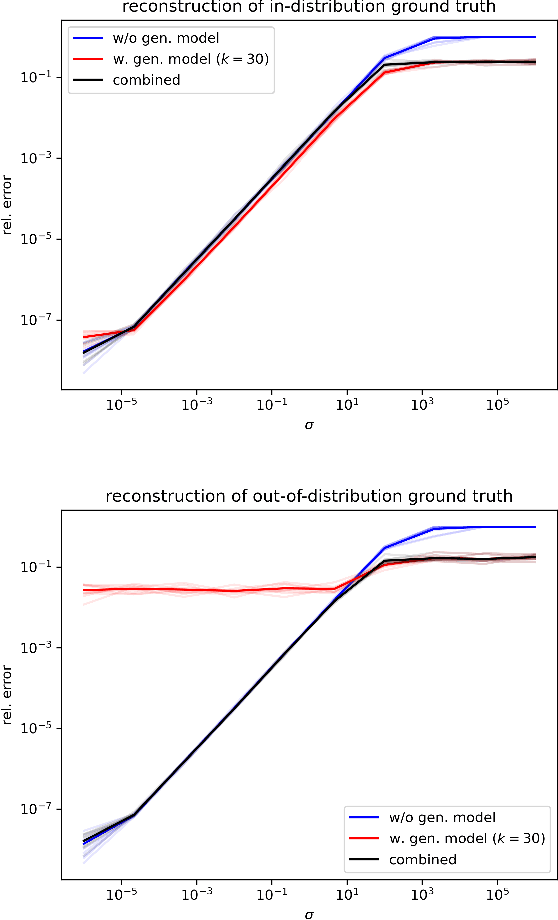
Abstract:In phase retrieval and similar inverse problems, the stability of solutions across different noise levels is crucial for applications. One approach to promote it is using signal priors in a form of a generative model as a regularization, at the expense of introducing a bias in the reconstruction. In this paper, we explore and compare the reconstruction properties of classical and generative inverse problem formulations. We propose a new unified reconstruction approach that mitigates overfitting to the generative model for varying noise levels.
On best approximation by multivariate ridge functions with applications to generalized translation networks
Dec 11, 2024Abstract:We prove sharp upper and lower bounds for the approximation of Sobolev functions by sums of multivariate ridge functions, i.e., functions of the form $\mathbb{R}^d \ni x \mapsto \sum_{k=1}^n h_k(A_k x) \in \mathbb{R}$ with $h_k : \mathbb{R}^\ell \to \mathbb{R}$ and $A_k \in \mathbb{R}^{\ell \times d}$. We show that the order of approximation asymptotically behaves as $n^{-r/(d-\ell)}$, where $r$ is the regularity of the Sobolev functions to be approximated. Our lower bound even holds when approximating $L^\infty$-Sobolev functions of regularity $r$ with error measured in $L^1$, while our upper bound applies to the approximation of $L^p$-Sobolev functions in $L^p$ for any $1 \leq p \leq \infty$. These bounds generalize well-known results about the approximation properties of univariate ridge functions to the multivariate case. Moreover, we use these bounds to obtain sharp asymptotic bounds for the approximation of Sobolev functions using generalized translation networks and complex-valued neural networks.
Efficient uniform approximation using Random Vector Functional Link networks
Jun 30, 2023Abstract:A Random Vector Functional Link (RVFL) network is a depth-2 neural network with random inner weights and biases. As only the outer weights of such architectures need to be learned, the learning process boils down to a linear optimization task, allowing one to sidestep the pitfalls of nonconvex optimization problems. In this paper, we prove that an RVFL with ReLU activation functions can approximate Lipschitz continuous functions provided its hidden layer is exponentially wide in the input dimension. Although it has been established before that such approximation can be achieved in $L_2$ sense, we prove it for $L_\infty$ approximation error and Gaussian inner weights. To the best of our knowledge, our result is the first of this kind. We give a nonasymptotic lower bound for the number of hidden layer nodes, depending on, among other things, the Lipschitz constant of the target function, the desired accuracy, and the input dimension. Our method of proof is rooted in probability theory and harmonic analysis.
On audio enhancement via online non-negative matrix factorization
Oct 07, 2021
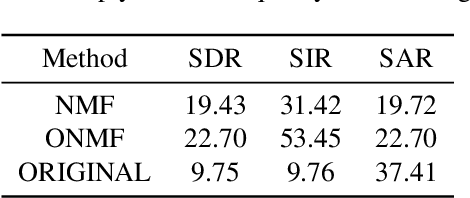
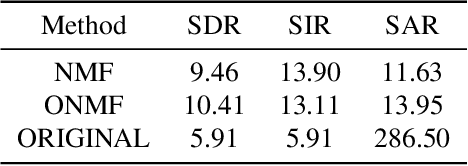

Abstract:We propose a method for noise reduction, the task of producing a clean audio signal from a recording corrupted by additive noise. Many common approaches to this problem are based upon applying non-negative matrix factorization to spectrogram measurements. These methods use a noiseless recording, which is believed to be similar in structure to the signal of interest, and a pure-noise recording to learn dictionaries for the true signal and the noise. One may then construct an approximation of the true signal by projecting the corrupted recording on to the clean dictionary. In this work, we build upon these methods by proposing the use of \emph{online} non-negative matrix factorization for this problem. This method is more memory efficient than traditional non-negative matrix factorization and also has potential applications to real-time denoising.
Random Vector Functional Link Networks for Function Approximation on Manifolds
Jul 30, 2020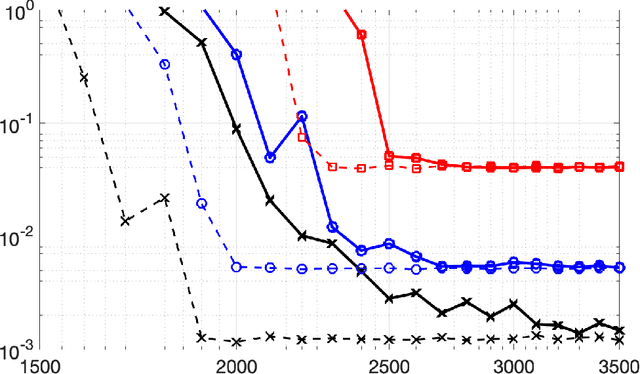
Abstract:The learning speed of feed-forward neural networks is notoriously slow and has presented a bottleneck in deep learning applications for several decades. For instance, gradient-based learning algorithms, which are used extensively to train neural networks, tend to work slowly when all of the network parameters must be iteratively tuned. To counter this, both researchers and practitioners have tried introducing randomness to reduce the learning requirement. Based on the original construction of Igelnik and Pao, single layer neural-networks with random input-to-hidden layer weights and biases have seen success in practice, but the necessary theoretical justification is lacking. In this paper, we begin to fill this theoretical gap. We provide a (corrected) rigorous proof that the Igelnik and Pao construction is a universal approximator for continuous functions on compact domains, with approximation error decaying asymptotically like $O(1/\sqrt{n})$ for the number $n$ of network nodes. We then extend this result to the non-asymptotic setting, proving that one can achieve any desired approximation error with high probability provided $n$ is sufficiently large. We further adapt this randomized neural network architecture to approximate functions on smooth, compact submanifolds of Euclidean space, providing theoretical guarantees in both the asymptotic and non-asymptotic forms. Finally, we illustrate our results on manifolds with numerical experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge