Accumulator-Aware Post-Training Quantization

Several recent studies have investigated low-precision accumulation, reporting improvements in throughput, power, and area across various platforms. However, the accompanying proposals have only considered the quantization-aware training (QAT) paradigm, in which models are fine-tuned or trained from scratch with quantization in the loop. As models continue to grow in size, QAT techniques become increasingly more expensive, which has motivated the recent surge in post-training quantization (PTQ) research. To the best of our knowledge, ours marks the first formal study of accumulator-aware quantization in the PTQ setting. To bridge this gap, we introduce AXE, a practical framework of accumulator-aware extensions designed to endow overflow avoidance guarantees to existing layer-wise PTQ algorithms. We theoretically motivate AXE and demonstrate its flexibility by implementing it on top of two state-of-the-art PTQ algorithms: GPFQ and OPTQ. We further generalize AXE to support multi-stage accumulation for the first time, opening the door for full datapath optimization and scaling to large language models (LLMs). We evaluate AXE across image classification and language generation models, and observe significant improvements in the trade-off between accumulator bit width and model accuracy over baseline methods.

SPFQ: A Stochastic Algorithm and Its Error Analysis for Neural Network Quantization

Quantization is a widely used compression method that effectively reduces redundancies in over-parameterized neural networks. However, existing quantization techniques for deep neural networks often lack a comprehensive error analysis due to the presence of non-convex loss functions and nonlinear activations. In this paper, we propose a fast stochastic algorithm for quantizing the weights of fully trained neural networks. Our approach leverages a greedy path-following mechanism in combination with a stochastic quantizer. Its computational complexity scales only linearly with the number of weights in the network, thereby enabling the efficient quantization of large networks. Importantly, we establish, for the first time, full-network error bounds, under an infinite alphabet condition and minimal assumptions on the weights and input data. As an application of this result, we prove that when quantizing a multi-layer network having Gaussian weights, the relative square quantization error exhibits a linear decay as the degree of over-parametrization increases. Furthermore, we demonstrate that it is possible to achieve error bounds equivalent to those obtained in the infinite alphabet case, using on the order of a mere $\log\log N$ bits per weight, where $N$ represents the largest number of neurons in a layer.

A simple approach for quantizing neural networks

In this short note, we propose a new method for quantizing the weights of a fully trained neural network. A simple deterministic pre-processing step allows us to quantize network layers via memoryless scalar quantization while preserving the network performance on given training data. On one hand, the computational complexity of this pre-processing slightly exceeds that of state-of-the-art algorithms in the literature. On the other hand, our approach does not require any hyper-parameter tuning and, in contrast to previous methods, allows a plain analysis. We provide rigorous theoretical guarantees in the case of quantizing single network layers and show that the relative error decays with the number of parameters in the network if the training data behaves well, e.g., if it is sampled from suitable random distributions. The developed method also readily allows the quantization of deep networks by consecutive application to single layers.

Spectrally Adaptive Common Spatial Patterns

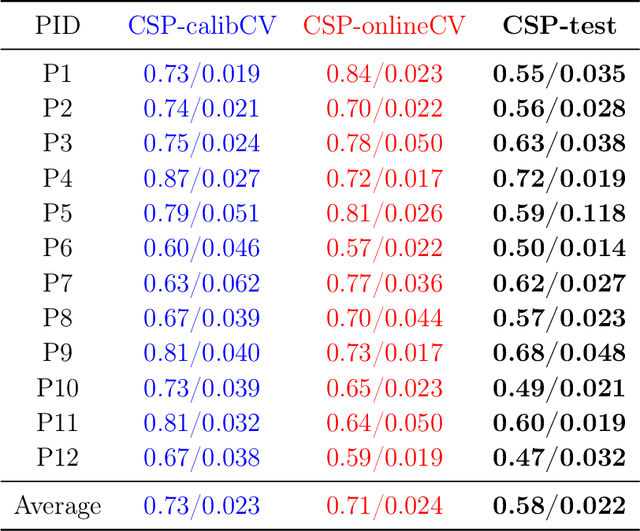
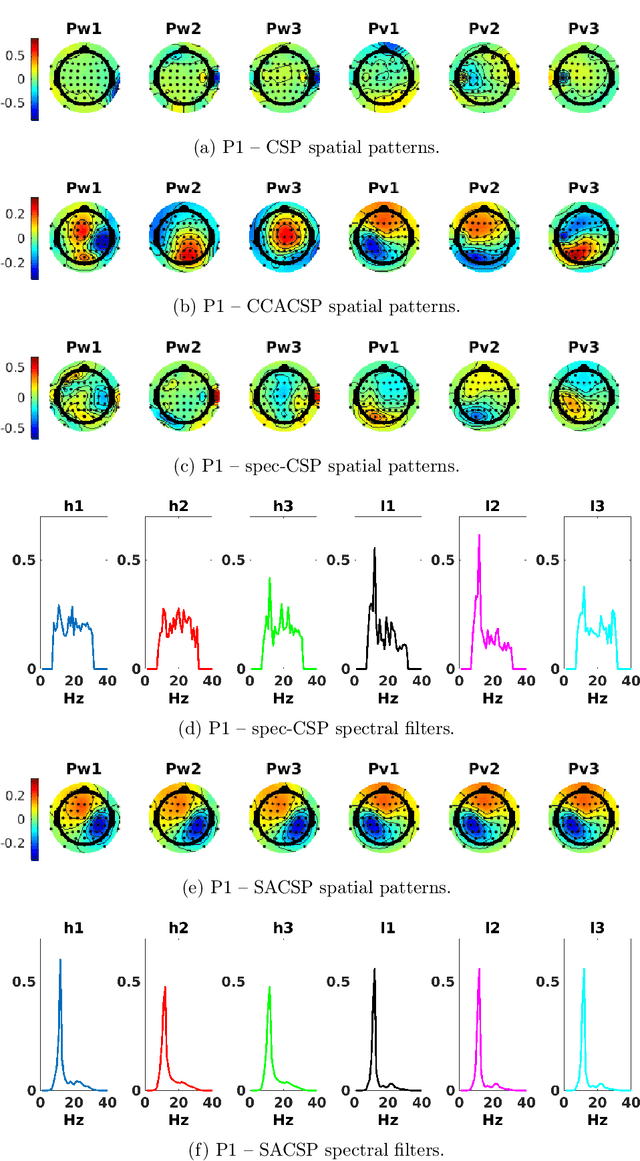
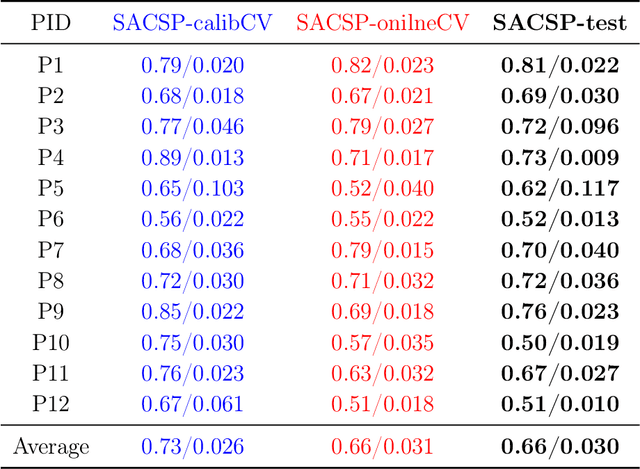
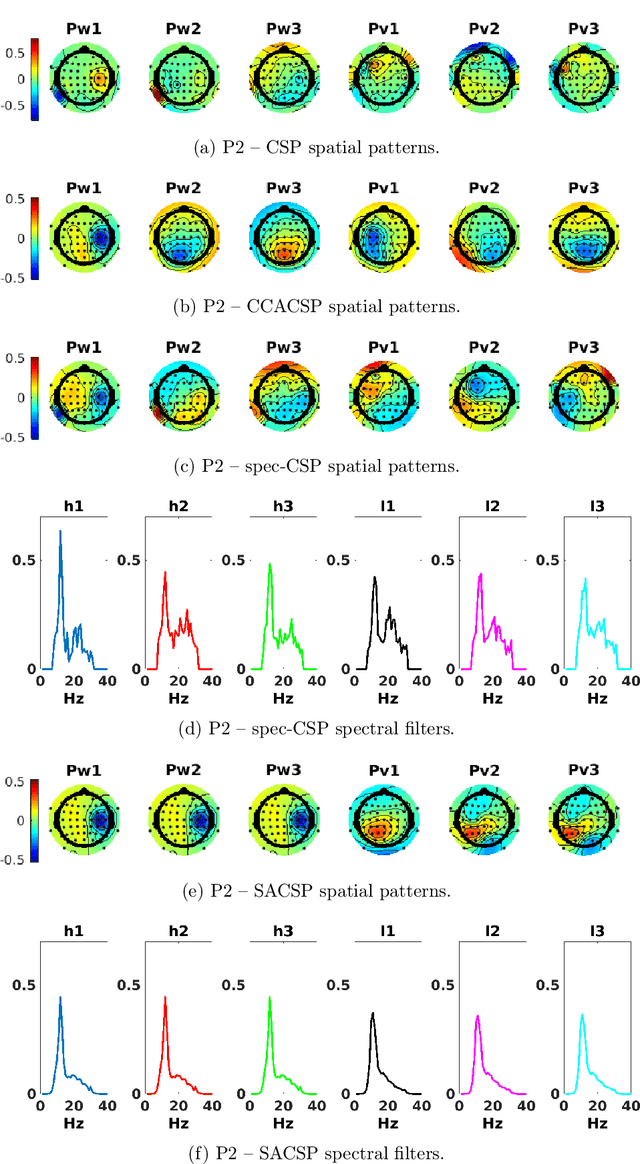
The method of Common Spatial Patterns (CSP) is widely used for feature extraction of electroencephalography (EEG) data, such as in motor imagery brain-computer interface (BCI) systems. It is a data-driven method estimating a set of spatial filters so that the power of the filtered EEG signal is maximized for one motor imagery class and minimized for the other. This method, however, is prone to overfitting and is known to suffer from poor generalization especially with limited calibration data. Additionally, due to the high heterogeneity in brain data and the non-stationarity of brain activity, CSP is usually trained for each user separately resulting in long calibration sessions or frequent re-calibrations that are tiring for the user. In this work, we propose a novel algorithm called Spectrally Adaptive Common Spatial Patterns (SACSP) that improves CSP by learning a temporal/spectral filter for each spatial filter so that the spatial filters are concentrated on the most relevant temporal frequencies for each user. We show the efficacy of SACSP in providing better generalizability and higher classification accuracy from calibration to online control compared to existing methods. Furthermore, we show that SACSP provides neurophysiologically relevant information about the temporal frequencies of the filtered signals. Our results highlight the differences in the motor imagery signal among BCI users as well as spectral differences in the signals generated for each class, and show the importance of learning robust user-specific features in a data-driven manner.

Post-training Quantization for Neural Networks with Provable Guarantees

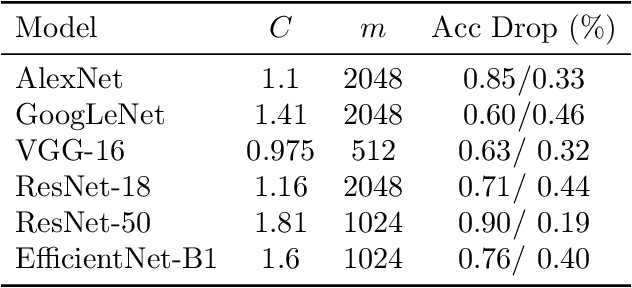
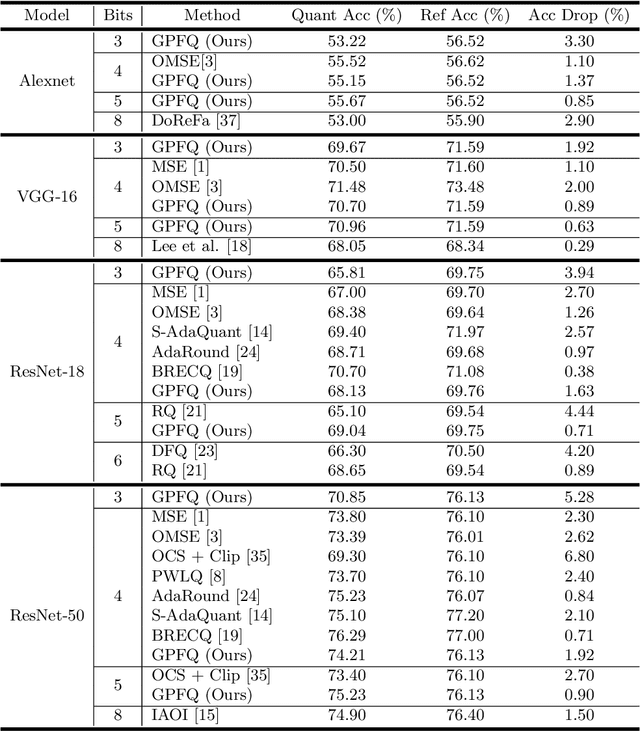
While neural networks have been remarkably successful in a wide array of applications, implementing them in resource-constrained hardware remains an area of intense research. By replacing the weights of a neural network with quantized (e.g., 4-bit, or binary) counterparts, massive savings in computation cost, memory, and power consumption are attained. We modify a post-training neural-network quantization method, GPFQ, that is based on a greedy path-following mechanism, and rigorously analyze its error. We prove that for quantizing a single-layer network, the relative square error essentially decays linearly in the number of weights -- i.e., level of over-parametrization. Our result holds across a range of input distributions and for both fully-connected and convolutional architectures. To empirically evaluate the method, we quantize several common architectures with few bits per weight, and test them on ImageNet, showing only minor loss of accuracy. We also demonstrate that standard modifications, such as bias correction and mixed precision quantization, further improve accuracy.

Sigma-Delta and Distributed Noise-Shaping Quantization Methods for Random Fourier Features

We propose the use of low bit-depth Sigma-Delta and distributed noise-shaping methods for quantizing the Random Fourier features (RFFs) associated with shift-invariant kernels. We prove that our quantized RFFs -- even in the case of $1$-bit quantization -- allow a high accuracy approximation of the underlying kernels, and the approximation error decays at least polynomially fast as the dimension of the RFFs increases. We also show that the quantized RFFs can be further compressed, yielding an excellent trade-off between memory use and accuracy. Namely, the approximation error now decays exponentially as a function of the bits used. Moreover, we empirically show by testing the performance of our methods on several machine learning tasks that our method compares favorably to other state of the art quantization methods in this context.

A Greedy Algorithm for Quantizing Neural Networks

We propose a new computationally efficient method for quantizing the weights of pre-trained neural networks that is general enough to handle both multi-layer perceptrons and convolutional neural networks. Our method deterministically quantizes layers in an iterative fashion with no complicated re-training required. Specifically, we quantize each neuron, or hidden unit, using a greedy path-following algorithm. This simple algorithm is equivalent to running a dynamical system, which we prove is stable for quantizing a single-layer neural network (or, alternatively, for quantizing the first layer of a multi-layer network) when the training data are Gaussian. We show that under these assumptions, the quantization error decays with the width of the layer, i.e., its level of over-parametrization. We provide numerical experiments, on multi-layer networks, to illustrate the performance of our methods on MNIST and CIFAR10 data.

Faster Binary Embeddings for Preserving Euclidean Distances

We propose a fast, distance-preserving, binary embedding algorithm to transform a high-dimensional dataset $\mathcal{T}\subseteq\mathbb{R}^n$ into binary sequences in the cube $\{\pm 1\}^m$. When $\mathcal{T}$ consists of well-spread (i.e., non-sparse) vectors, our embedding method applies a stable noise-shaping quantization scheme to $A x$ where $A\in\mathbb{R}^{m\times n}$ is a sparse Gaussian random matrix. This contrasts with most binary embedding methods, which usually use $x\mapsto \mathrm{sign}(Ax)$ for the embedding. Moreover, we show that Euclidean distances among the elements of $\mathcal{T}$ are approximated by the $\ell_1$ norm on the images of $\{\pm 1\}^m$ under a fast linear transformation. This again contrasts with standard methods, where the Hamming distance is used instead. Our method is both fast and memory efficient, with time complexity $O(m)$ and space complexity $O(m)$. Further, we prove that the method is accurate and its associated error is comparable to that of a continuous valued Johnson-Lindenstrauss embedding plus a quantization error that admits a polynomial decay as the embedding dimension $m$ increases. Thus the length of the binary codes required to achieve a desired accuracy is quite small, and we show it can even be compressed further without compromising the accuracy. To illustrate our results, we test the proposed method on natural images and show that it achieves strong performance.

Random Vector Functional Link Networks for Function Approximation on Manifolds

The learning speed of feed-forward neural networks is notoriously slow and has presented a bottleneck in deep learning applications for several decades. For instance, gradient-based learning algorithms, which are used extensively to train neural networks, tend to work slowly when all of the network parameters must be iteratively tuned. To counter this, both researchers and practitioners have tried introducing randomness to reduce the learning requirement. Based on the original construction of Igelnik and Pao, single layer neural-networks with random input-to-hidden layer weights and biases have seen success in practice, but the necessary theoretical justification is lacking. In this paper, we begin to fill this theoretical gap. We provide a (corrected) rigorous proof that the Igelnik and Pao construction is a universal approximator for continuous functions on compact domains, with approximation error decaying asymptotically like $O(1/\sqrt{n})$ for the number $n$ of network nodes. We then extend this result to the non-asymptotic setting, proving that one can achieve any desired approximation error with high probability provided $n$ is sufficiently large. We further adapt this randomized neural network architecture to approximate functions on smooth, compact submanifolds of Euclidean space, providing theoretical guarantees in both the asymptotic and non-asymptotic forms. Finally, we illustrate our results on manifolds with numerical experiments.

Fast binary embeddings, and quantized compressed sensing with structured matrices

This paper deals with two related problems, namely distance-preserving binary embeddings and quantization for compressed sensing . First, we propose fast methods to replace points from a subset $\mathcal{X} \subset \mathbb{R}^n$, associated with the Euclidean metric, with points in the cube $\{\pm 1\}^m$ and we associate the cube with a pseudo-metric that approximates Euclidean distance among points in $\mathcal{X}$. Our methods rely on quantizing fast Johnson-Lindenstrauss embeddings based on bounded orthonormal systems and partial circulant ensembles, both of which admit fast transforms. Our quantization methods utilize noise-shaping, and include Sigma-Delta schemes and distributed noise-shaping schemes. The resulting approximation errors decay polynomially and exponentially fast in $m$, depending on the embedding method. This dramatically outperforms the current decay rates associated with binary embeddings and Hamming distances. Additionally, it is the first such binary embedding result that applies to fast Johnson-Lindenstrauss maps while preserving $\ell_2$ norms. Second, we again consider noise-shaping schemes, albeit this time to quantize compressed sensing measurements arising from bounded orthonormal ensembles and partial circulant matrices. We show that these methods yield a reconstruction error that again decays with the number of measurements (and bits), when using convex optimization for reconstruction. Specifically, for Sigma-Delta schemes, the error decays polynomially in the number of measurements, and it decays exponentially for distributed noise-shaping schemes based on beta encoding. These results are near optimal and the first of their kind dealing with bounded orthonormal systems.