Encoding Argumentation Frameworks to Propositional Logic Systems

The theory of argumentation frameworks ($AF$s) has been a useful tool for artificial intelligence. The research of the connection between $AF$s and logic is an important branch. This paper generalizes the encoding method by encoding $AF$s as logical formulas in different propositional logic systems. It studies the relationship between models of an AF by argumentation semantics, including Dung's classical semantics and Gabbay's equational semantics, and models of the encoded formulas by semantics of propositional logic systems. Firstly, we supplement the proof of the regular encoding function in the case of encoding $AF$s to the 2-valued propositional logic system. Then we encode $AF$s to 3-valued propositional logic systems and fuzzy propositional logic systems and explore the model relationship. This paper enhances the connection between $AF$s and propositional logic systems. It also provides a new way to construct new equational semantics by choosing different fuzzy logic operations.

Imagen 3

We introduce Imagen 3, a latent diffusion model that generates high quality images from text prompts. We describe our quality and responsibility evaluations. Imagen 3 is preferred over other state-of-the-art (SOTA) models at the time of evaluation. In addition, we discuss issues around safety and representation, as well as methods we used to minimize the potential harm of our models.

Reconstruction Attacks on Machine Unlearning: Simple Models are Vulnerable

Machine unlearning is motivated by desire for data autonomy: a person can request to have their data's influence removed from deployed models, and those models should be updated as if they were retrained without the person's data. We show that, counter-intuitively, these updates expose individuals to high-accuracy reconstruction attacks which allow the attacker to recover their data in its entirety, even when the original models are so simple that privacy risk might not otherwise have been a concern. We show how to mount a near-perfect attack on the deleted data point from linear regression models. We then generalize our attack to other loss functions and architectures, and empirically demonstrate the effectiveness of our attacks across a wide range of datasets (capturing both tabular and image data). Our work highlights that privacy risk is significant even for extremely simple model classes when individuals can request deletion of their data from the model.

Membership Inference Attacks on Diffusion Models via Quantile Regression

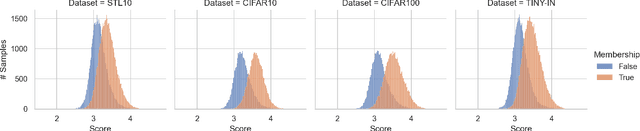
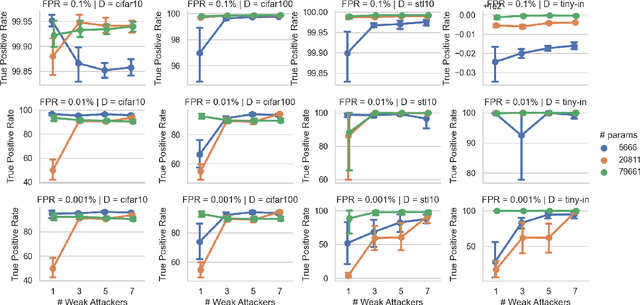
Recently, diffusion models have become popular tools for image synthesis because of their high-quality outputs. However, like other large-scale models, they may leak private information about their training data. Here, we demonstrate a privacy vulnerability of diffusion models through a \emph{membership inference (MI) attack}, which aims to identify whether a target example belongs to the training set when given the trained diffusion model. Our proposed MI attack learns quantile regression models that predict (a quantile of) the distribution of reconstruction loss on examples not used in training. This allows us to define a granular hypothesis test for determining the membership of a point in the training set, based on thresholding the reconstruction loss of that point using a custom threshold tailored to the example. We also provide a simple bootstrap technique that takes a majority membership prediction over ``a bag of weak attackers'' which improves the accuracy over individual quantile regression models. We show that our attack outperforms the prior state-of-the-art attack while being substantially less computationally expensive -- prior attacks required training multiple ``shadow models'' with the same architecture as the model under attack, whereas our attack requires training only much smaller models.

Scalable Membership Inference Attacks via Quantile Regression

Membership inference attacks are designed to determine, using black box access to trained models, whether a particular example was used in training or not. Membership inference can be formalized as a hypothesis testing problem. The most effective existing attacks estimate the distribution of some test statistic (usually the model's confidence on the true label) on points that were (and were not) used in training by training many \emph{shadow models} -- i.e. models of the same architecture as the model being attacked, trained on a random subsample of data. While effective, these attacks are extremely computationally expensive, especially when the model under attack is large. We introduce a new class of attacks based on performing quantile regression on the distribution of confidence scores induced by the model under attack on points that are not used in training. We show that our method is competitive with state-of-the-art shadow model attacks, while requiring substantially less compute because our attack requires training only a single model. Moreover, unlike shadow model attacks, our proposed attack does not require any knowledge of the architecture of the model under attack and is therefore truly ``black-box". We show the efficacy of this approach in an extensive series of experiments on various datasets and model architectures.

Improved Differentially Private Regression via Gradient Boosting

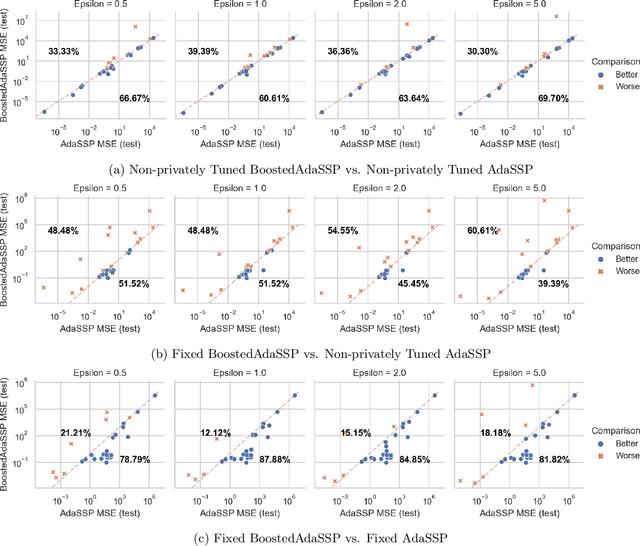
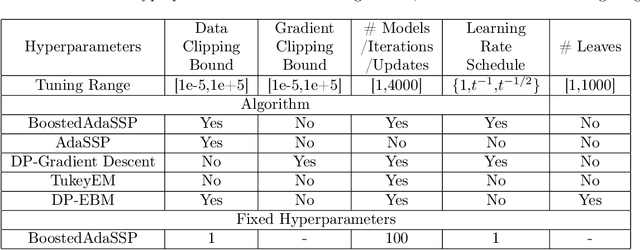
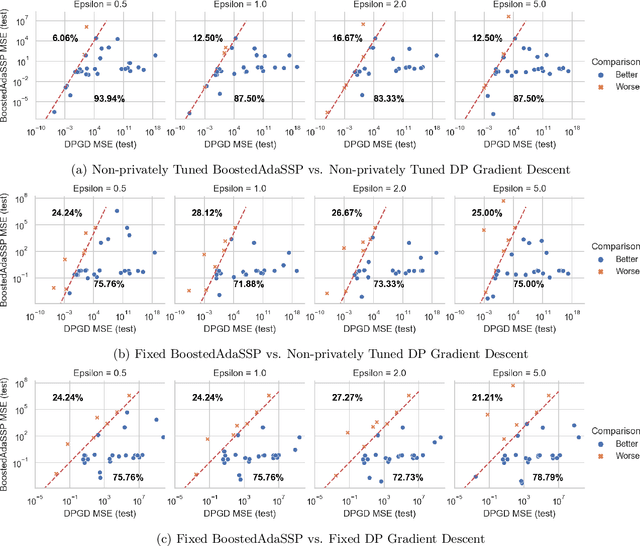
We revisit the problem of differentially private squared error linear regression. We observe that existing state-of-the-art methods are sensitive to the choice of hyper-parameters -- including the ``clipping threshold'' that cannot be set optimally in a data-independent way. We give a new algorithm for private linear regression based on gradient boosting. We show that our method consistently improves over the previous state of the art when the clipping threshold is taken to be fixed without knowledge of the data, rather than optimized in a non-private way -- and that even when we optimize the clipping threshold non-privately, our algorithm is no worse. In addition to a comprehensive set of experiments, we give theoretical insights to explain this behavior.

Private Synthetic Data for Multitask Learning and Marginal Queries

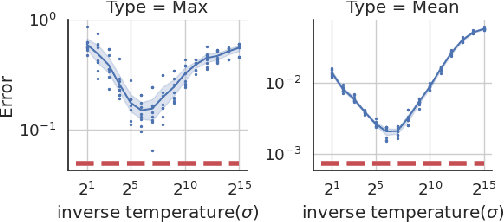
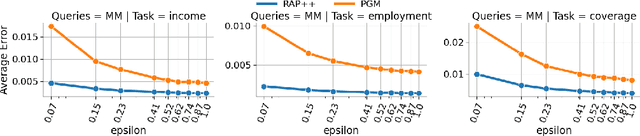
We provide a differentially private algorithm for producing synthetic data simultaneously useful for multiple tasks: marginal queries and multitask machine learning (ML). A key innovation in our algorithm is the ability to directly handle numerical features, in contrast to a number of related prior approaches which require numerical features to be first converted into {high cardinality} categorical features via {a binning strategy}. Higher binning granularity is required for better accuracy, but this negatively impacts scalability. Eliminating the need for binning allows us to produce synthetic data preserving large numbers of statistical queries such as marginals on numerical features, and class conditional linear threshold queries. Preserving the latter means that the fraction of points of each class label above a particular half-space is roughly the same in both the real and synthetic data. This is the property that is needed to train a linear classifier in a multitask setting. Our algorithm also allows us to produce high quality synthetic data for mixed marginal queries, that combine both categorical and numerical features. Our method consistently runs 2-5x faster than the best comparable techniques, and provides significant accuracy improvements in both marginal queries and linear prediction tasks for mixed-type datasets.

MAMDR: A Model Agnostic Learning Method for Multi-Domain Recommendation

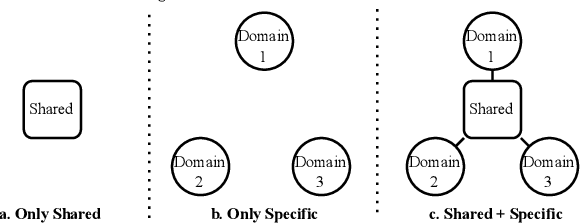
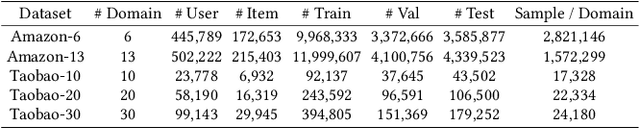
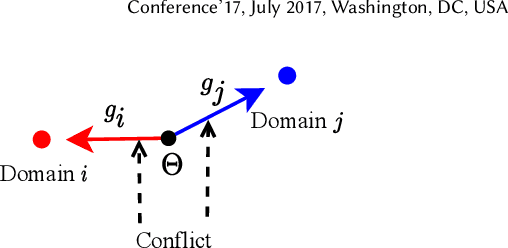
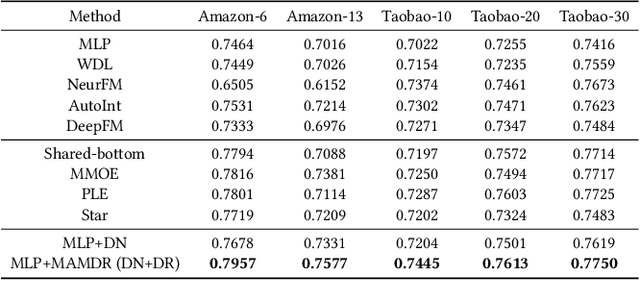
Large-scale e-commercial platforms in the real-world usually contain various recommendation scenarios (domains) to meet demands of diverse customer groups. Multi-Domain Recommendation (MDR), which aims to jointly improve recommendations on all domains, has attracted increasing attention from practitioners and researchers. Existing MDR methods often employ a shared structure to leverage reusable features for all domains and several specific parts to capture domain-specific information. However, data from different domains may conflict with each other and cause shared parameters to stay at a compromised position on the optimization landscape. This could deteriorate the overall performance. Despite the specific parameters are separately learned for each domain, they can easily overfit on data sparsity domains. Furthermore, data distribution differs across domains, making it challenging to develop a general model that can be applied to all circumstances. To address these problems, we propose a novel model agnostic learning method, namely MAMDR, for the multi-domain recommendation. Specifically, we first propose a Domain Negotiation (DN) strategy to alleviate the conflict between domains and learn better shared parameters. Then, we develop a Domain Regularization (DR) scheme to improve the generalization ability of specific parameters by learning from other domains. Finally, we integrate these components into a unified framework and present MAMDR which can be applied to any model structure to perform multi-domain recommendation. Extensive experiments on various real-world datasets and online applications demonstrate both the effectiveness and generalizability of MAMDR.

Spectrally Adaptive Common Spatial Patterns

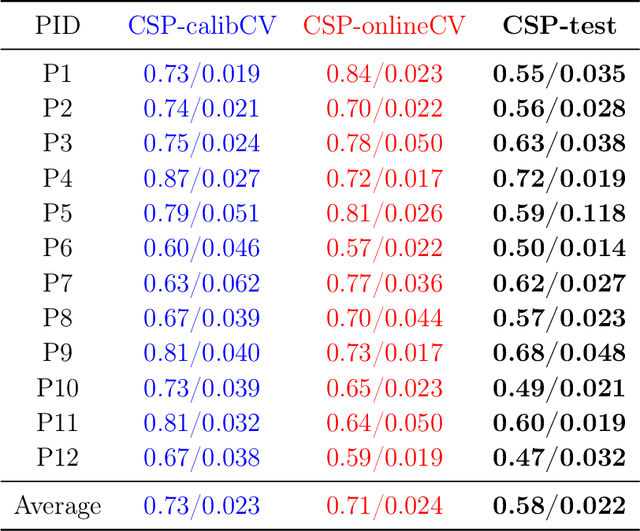
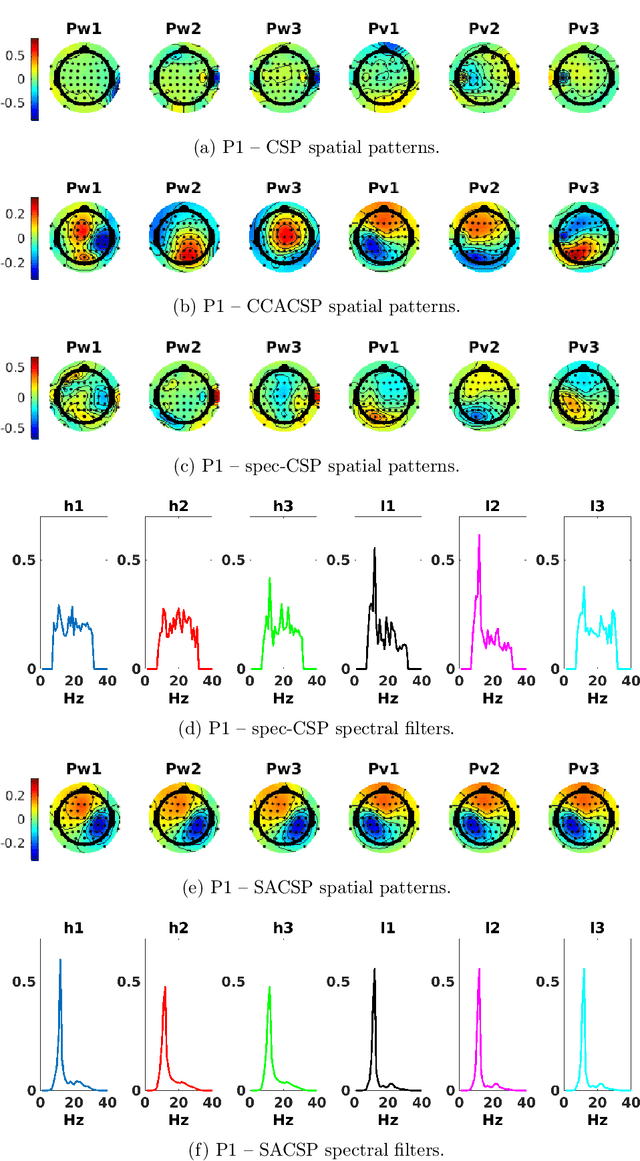
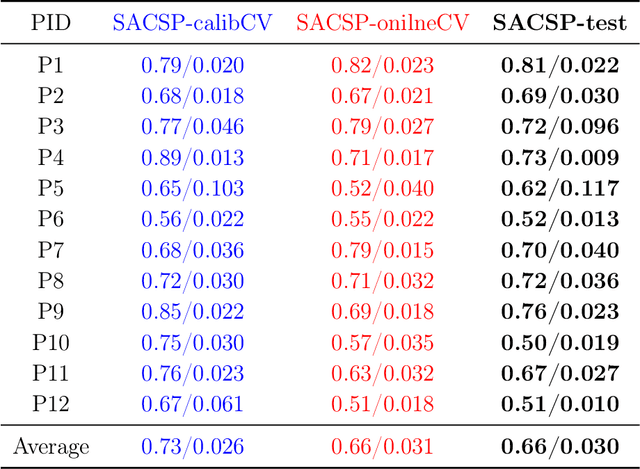
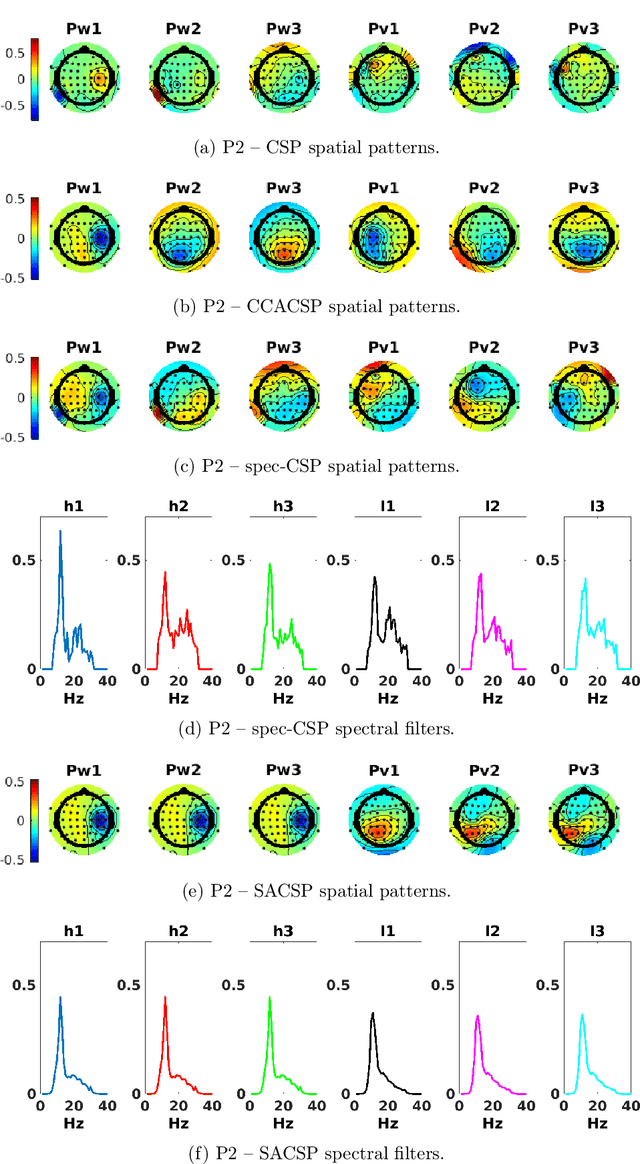
The method of Common Spatial Patterns (CSP) is widely used for feature extraction of electroencephalography (EEG) data, such as in motor imagery brain-computer interface (BCI) systems. It is a data-driven method estimating a set of spatial filters so that the power of the filtered EEG signal is maximized for one motor imagery class and minimized for the other. This method, however, is prone to overfitting and is known to suffer from poor generalization especially with limited calibration data. Additionally, due to the high heterogeneity in brain data and the non-stationarity of brain activity, CSP is usually trained for each user separately resulting in long calibration sessions or frequent re-calibrations that are tiring for the user. In this work, we propose a novel algorithm called Spectrally Adaptive Common Spatial Patterns (SACSP) that improves CSP by learning a temporal/spectral filter for each spatial filter so that the spatial filters are concentrated on the most relevant temporal frequencies for each user. We show the efficacy of SACSP in providing better generalizability and higher classification accuracy from calibration to online control compared to existing methods. Furthermore, we show that SACSP provides neurophysiologically relevant information about the temporal frequencies of the filtered signals. Our results highlight the differences in the motor imagery signal among BCI users as well as spectral differences in the signals generated for each class, and show the importance of learning robust user-specific features in a data-driven manner.

Fast Adaptation with Linearized Neural Networks

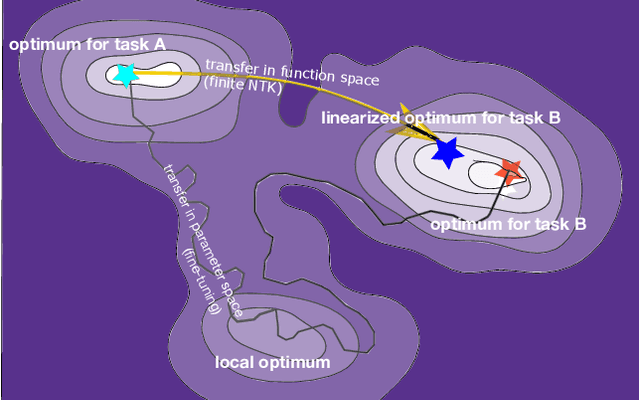
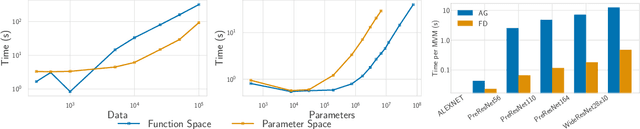
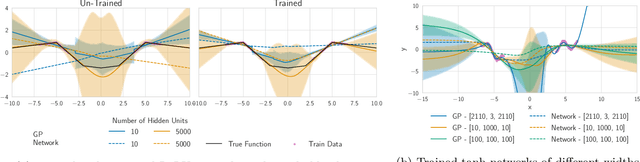
The inductive biases of trained neural networks are difficult to understand and, consequently, to adapt to new settings. We study the inductive biases of linearizations of neural networks, which we show to be surprisingly good summaries of the full network functions. Inspired by this finding, we propose a technique for embedding these inductive biases into Gaussian processes through a kernel designed from the Jacobian of the network. In this setting, domain adaptation takes the form of interpretable posterior inference, with accompanying uncertainty estimation. This inference is analytic and free of local optima issues found in standard techniques such as fine-tuning neural network weights to a new task. We develop significant computational speed-ups based on matrix multiplies, including a novel implementation for scalable Fisher vector products. Our experiments on both image classification and regression demonstrate the promise and convenience of this framework for transfer learning, compared to neural network fine-tuning. Code is available at https://github.com/amzn/xfer/tree/master/finite_ntk.