Online Stackelberg Optimization via Nonlinear Control

In repeated interaction problems with adaptive agents, our objective often requires anticipating and optimizing over the space of possible agent responses. We show that many problems of this form can be cast as instances of online (nonlinear) control which satisfy \textit{local controllability}, with convex losses over a bounded state space which encodes agent behavior, and we introduce a unified algorithmic framework for tractable regret minimization in such cases. When the instance dynamics are known but otherwise arbitrary, we obtain oracle-efficient $O(\sqrt{T})$ regret by reduction to online convex optimization, which can be made computationally efficient if dynamics are locally \textit{action-linear}. In the presence of adversarial disturbances to the state, we give tight bounds in terms of either the cumulative or per-round disturbance magnitude (for \textit{strongly} or \textit{weakly} locally controllable dynamics, respectively). Additionally, we give sublinear regret results for the cases of unknown locally action-linear dynamics as well as for the bandit feedback setting. Finally, we demonstrate applications of our framework to well-studied problems including performative prediction, recommendations for adaptive agents, adaptive pricing of real-valued goods, and repeated gameplay against no-regret learners, directly yielding extensions beyond prior results in each case.

Is Learning in Games Good for the Learners?

We consider a number of questions related to tradeoffs between reward and regret in repeated gameplay between two agents. To facilitate this, we introduce a notion of {\it generalized equilibrium} which allows for asymmetric regret constraints, and yields polytopes of feasible values for each agent and pair of regret constraints, where we show that any such equilibrium is reachable by a pair of algorithms which maintain their regret guarantees against arbitrary opponents. As a central example, we highlight the case one agent is no-swap and the other's regret is unconstrained. We show that this captures an extension of {\it Stackelberg} equilibria with a matching optimal value, and that there exists a wide class of games where a player can significantly increase their utility by deviating from a no-swap-regret algorithm against a no-swap learner (in fact, almost any game without pure Nash equilibria is of this form). Additionally, we make use of generalized equilibria to consider tradeoffs in terms of the opponent's algorithm choice. We give a tight characterization for the maximal reward obtainable against {\it some} no-regret learner, yet we also show a class of games in which this is bounded away from the value obtainable against the class of common ``mean-based'' no-regret algorithms. Finally, we consider the question of learning reward-optimal strategies via repeated play with a no-regret agent when the game is initially unknown. Again we show tradeoffs depending on the opponent's learning algorithm: the Stackelberg strategy is learnable in exponential time with any no-regret agent (and in polynomial time with any no-{\it adaptive}-regret agent) for any game where it is learnable via queries, and there are games where it is learnable in polynomial time against any no-swap-regret agent but requires exponential time against a mean-based no-regret agent.

Online Recommendations for Agents with Discounted Adaptive Preferences

For domains in which a recommender provides repeated content suggestions, agent preferences may evolve over time as a function of prior recommendations, and algorithms must take this into account for long-run optimization. Recently, Agarwal and Brown (2022) introduced a model for studying recommendations when agents' preferences are adaptive, and gave a series of results for the case when agent preferences depend {\it uniformly} on their history of past selections. Here, the recommender shows a $k$-item menu (out of $n$) to the agent at each round, who selects one of the $k$ items via their history-dependent {\it preference model}, yielding a per-item adversarial reward for the recommender. We expand this setting to {\it non-uniform} preferences, and give a series of results for {\it $\gamma$-discounted} histories. For this problem, the feasible regret benchmarks can depend drastically on varying conditions. In the ``large $\gamma$'' regime, we show that the previously considered benchmark, the ``EIRD set'', is attainable for any {\it smooth} model, relaxing the ``local learnability'' requirement from the uniform memory case. We introduce ``pseudo-increasing'' preference models, for which we give an algorithm which can compete against any item distribution with small uniform noise (the ``smoothed simplex''). We show NP-hardness results for larger regret benchmarks in each case. We give another algorithm for pseudo-increasing models (under a restriction on the adversarial nature of the reward functions), which works for any $\gamma$ and is faster when $\gamma$ is sufficiently small, and we show a super-polynomial regret lower bound with respect to EIRD for general models in the ``small $\gamma$'' regime. We conclude with a pair of algorithms for the memoryless case.

Forecasting West Nile Virus with Graph Neural Networks: Harnessing Spatial Dependence in Irregularly Sampled Geospatial Data

Machine learning methods have seen increased application to geospatial environmental problems, such as precipitation nowcasting, haze forecasting, and crop yield prediction. However, many of the machine learning methods applied to mosquito population and disease forecasting do not inherently take into account the underlying spatial structure of the given data. In our work, we apply a spatially aware graph neural network model consisting of GraphSAGE layers to forecast the presence of West Nile virus in Illinois, to aid mosquito surveillance and abatement efforts within the state. More generally, we show that graph neural networks applied to irregularly sampled geospatial data can exceed the performance of a range of baseline methods including logistic regression, XGBoost, and fully-connected neural networks.

Learning in Multi-Player Stochastic Games

We consider the problem of simultaneous learning in stochastic games with many players in the finite-horizon setting. While the typical target solution for a stochastic game is a Nash equilibrium, this is intractable with many players. We instead focus on variants of {\it correlated equilibria}, such as those studied for extensive-form games. We begin with a hardness result for the adversarial MDP problem: even for a horizon of 3, obtaining sublinear regret against the best non-stationary policy is \textsf{NP}-hard when both rewards and transitions are adversarial. This implies that convergence to even the weakest natural solution concept -- normal-form coarse correlated equilbrium -- is not possible via black-box reduction to a no-regret algorithm even in stochastic games with constant horizon (unless $\textsf{NP}\subseteq\textsf{BPP}$). Instead, we turn to a different target: algorithms which {\it generate} an equilibrium when they are used by all players. Our main result is algorithm which generates an {\it extensive-form} correlated equilibrium, whose runtime is exponential in the horizon but polynomial in all other parameters. We give a similar algorithm which is polynomial in all parameters for "fast-mixing" stochastic games. We also show a method for efficiently reaching normal-form coarse correlated equilibria in "single-controller" stochastic games which follows the traditional no-regret approach. When shared randomness is available, the two generative algorithms can be extended to give simultaneous regret bounds and converge in the traditional sense.

Private Synthetic Data for Multitask Learning and Marginal Queries

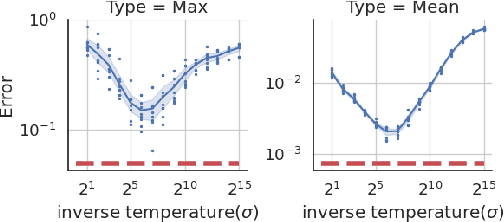
We provide a differentially private algorithm for producing synthetic data simultaneously useful for multiple tasks: marginal queries and multitask machine learning (ML). A key innovation in our algorithm is the ability to directly handle numerical features, in contrast to a number of related prior approaches which require numerical features to be first converted into {high cardinality} categorical features via {a binning strategy}. Higher binning granularity is required for better accuracy, but this negatively impacts scalability. Eliminating the need for binning allows us to produce synthetic data preserving large numbers of statistical queries such as marginals on numerical features, and class conditional linear threshold queries. Preserving the latter means that the fraction of points of each class label above a particular half-space is roughly the same in both the real and synthetic data. This is the property that is needed to train a linear classifier in a multitask setting. Our algorithm also allows us to produce high quality synthetic data for mixed marginal queries, that combine both categorical and numerical features. Our method consistently runs 2-5x faster than the best comparable techniques, and provides significant accuracy improvements in both marginal queries and linear prediction tasks for mixed-type datasets.

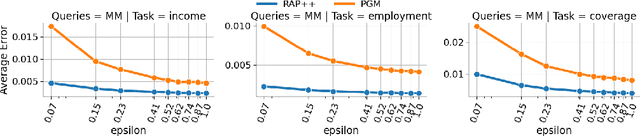
Differentially Private Query Release Through Adaptive Projection

We propose, implement, and evaluate a new algorithm for releasing answers to very large numbers of statistical queries like $k$-way marginals, subject to differential privacy. Our algorithm makes adaptive use of a continuous relaxation of the Projection Mechanism, which answers queries on the private dataset using simple perturbation, and then attempts to find the synthetic dataset that most closely matches the noisy answers. We use a continuous relaxation of the synthetic dataset domain which makes the projection loss differentiable, and allows us to use efficient ML optimization techniques and tooling. Rather than answering all queries up front, we make judicious use of our privacy budget by iteratively and adaptively finding queries for which our (relaxed) synthetic data has high error, and then repeating the projection. We perform extensive experimental evaluations across a range of parameters and datasets, and find that our method outperforms existing algorithms in many cases, especially when the privacy budget is small or the query class is large.

Painting Analysis Using Wavelets and Probabilistic Topic Models

In this paper, computer-based techniques for stylistic analysis of paintings are applied to the five panels of the 14th century Peruzzi Altarpiece by Giotto di Bondone. Features are extracted by combining a dual-tree complex wavelet transform with a hidden Markov tree (HMT) model. Hierarchical clustering is used to identify stylistic keywords in image patches, and keyword frequencies are calculated for sub-images that each contains many patches. A generative hierarchical Bayesian model learns stylistic patterns of keywords; these patterns are then used to characterize the styles of the sub-images; this in turn, permits to discriminate between paintings. Results suggest that such unsupervised probabilistic topic models can be useful to distill characteristic elements of style.