Simulated Language Acquisition in a Biologically Realistic Model of the Brain

Despite tremendous progress in neuroscience, we do not have a compelling narrative for the precise way whereby the spiking of neurons in our brain results in high-level cognitive phenomena such as planning and language. We introduce a simple mathematical formulation of six basic and broadly accepted principles of neuroscience: excitatory neurons, brain areas, random synapses, Hebbian plasticity, local inhibition, and inter-area inhibition. We implement a simulated neuromorphic system based on this formalism, which is capable of basic language acquisition: Starting from a tabula rasa, the system learns, in any language, the semantics of words, their syntactic role (verb versus noun), and the word order of the language, including the ability to generate novel sentences, through the exposure to a modest number of grounded sentences in the same language. We discuss several possible extensions and implications of this result.

Sink equilibria and the attractors of learning in games

Characterizing the limit behavior -- that is, the attractors -- of learning dynamics is one of the most fundamental open questions in game theory. In recent work in this front, it was conjectured that the attractors of the replicator dynamic are in one-to-one correspondence with the sink equilibria of the game -- the sink strongly connected components of a game's preference graph -- , and it was established that they do stand in at least one-to-many correspondence with them. We make threefold progress on the problem of characterizing attractors. First, we show through a topological construction that the one-to-one conjecture is false. Second, we make progress on the attractor characterization problem for two-player games by establishing that the one-to-one conjecture is true in the absence of a local pattern called a weak local source -- a pattern that is absent from zero-sum games. Finally, we look -- for the first time in this context -- at fictitious play, the longest-studied learning dynamic, and examine to what extent the conjecture generalizes there. We establish that under fictitious play, sink equilibria always contain attractors (sometimes strictly), and every attractor corresponds to a strongly connected set of nodes in the preference graph.

Charting the Shapes of Stories with Game Theory

Stories are records of our experiences and their analysis reveals insights into the nature of being human. Successful analyses are often interdisciplinary, leveraging mathematical tools to extract structure from stories and insights from structure. Historically, these tools have been restricted to one dimensional charts and dynamic social networks; however, modern AI offers the possibility of identifying more fully the plot structure, character incentives, and, importantly, counterfactual plot lines that the story could have taken but did not take. In this work, we use AI to model the structure of stories as game-theoretic objects, amenable to quantitative analysis. This allows us to not only interrogate each character's decision making, but also possibly peer into the original author's conception of the characters' world. We demonstrate our proposed technique on Shakespeare's famous Romeo and Juliet. We conclude with a discussion of how our analysis could be replicated in broader contexts, including real-life scenarios.

Swim till You Sink: Computing the Limit of a Game

During 2023, two interesting results were proven about the limit behavior of game dynamics: First, it was shown that there is a game for which no dynamics converges to the Nash equilibria. Second, it was shown that the sink equilibria of a game adequately capture the limit behavior of natural game dynamics. These two results have created a need and opportunity to articulate a principled computational theory of the meaning of the game that is based on game dynamics. Given any game in normal form, and any prior distribution of play, we study the problem of computing the asymptotic behavior of a class of natural dynamics called the noisy replicator dynamics as a limit distribution over the sink equilibria of the game. When the prior distribution has pure strategy support, we prove this distribution can be computed efficiently, in near-linear time to the size of the best-response graph. When the distribution can be sampled -- for example, if it is the uniform distribution over all mixed strategy profiles -- we show through experiments that the limit distribution of reasonably large games can be estimated quite accurately through sampling and simulation.

Online Stackelberg Optimization via Nonlinear Control

In repeated interaction problems with adaptive agents, our objective often requires anticipating and optimizing over the space of possible agent responses. We show that many problems of this form can be cast as instances of online (nonlinear) control which satisfy \textit{local controllability}, with convex losses over a bounded state space which encodes agent behavior, and we introduce a unified algorithmic framework for tractable regret minimization in such cases. When the instance dynamics are known but otherwise arbitrary, we obtain oracle-efficient $O(\sqrt{T})$ regret by reduction to online convex optimization, which can be made computationally efficient if dynamics are locally \textit{action-linear}. In the presence of adversarial disturbances to the state, we give tight bounds in terms of either the cumulative or per-round disturbance magnitude (for \textit{strongly} or \textit{weakly} locally controllable dynamics, respectively). Additionally, we give sublinear regret results for the cases of unknown locally action-linear dynamics as well as for the bandit feedback setting. Finally, we demonstrate applications of our framework to well-studied problems including performative prediction, recommendations for adaptive agents, adaptive pricing of real-valued goods, and repeated gameplay against no-regret learners, directly yielding extensions beyond prior results in each case.

Masked Generative Story Transformer with Character Guidance and Caption Augmentation

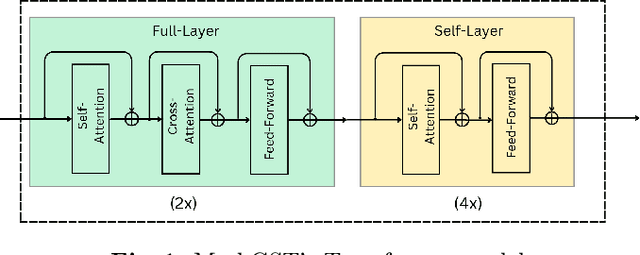
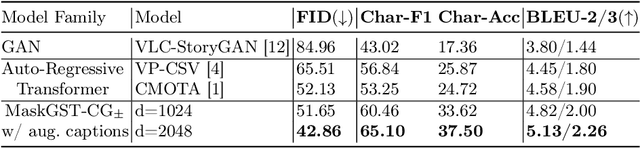
Story Visualization (SV) is a challenging generative vision task, that requires both visual quality and consistency between different frames in generated image sequences. Previous approaches either employ some kind of memory mechanism to maintain context throughout an auto-regressive generation of the image sequence, or model the generation of the characters and their background separately, to improve the rendering of characters. On the contrary, we embrace a completely parallel transformer-based approach, exclusively relying on Cross-Attention with past and future captions to achieve consistency. Additionally, we propose a Character Guidance technique to focus on the generation of characters in an implicit manner, by forming a combination of text-conditional and character-conditional logits in the logit space. We also employ a caption-augmentation technique, carried out by a Large Language Model (LLM), to enhance the robustness of our approach. The combination of these methods culminates into state-of-the-art (SOTA) results over various metrics in the most prominent SV benchmark (Pororo-SV), attained with constraint resources while achieving superior computational complexity compared to previous arts. The validity of our quantitative results is supported by a human survey.

On Limitations of the Transformer Architecture

What are the root causes of hallucinations in large language models (LLMs)? We use Communication Complexity to prove that the Transformer layer is incapable of composing functions (e.g., identify a grandparent of a person in a genealogy) if the domains of the functions are large enough; we show through examples that this inability is already empirically present when the domains are quite small. We also point out that several mathematical tasks that are at the core of the so-called compositional tasks thought to be hard for LLMs are unlikely to be solvable by Transformers, for large enough instances and assuming that certain well accepted conjectures in the field of Computational Complexity are true.

The complexity of non-stationary reinforcement learning

The problem of continual learning in the domain of reinforcement learning, often called non-stationary reinforcement learning, has been identified as an important challenge to the application of reinforcement learning. We prove a worst-case complexity result, which we believe captures this challenge: Modifying the probabilities or the reward of a single state-action pair in a reinforcement learning problem requires an amount of time almost as large as the number of states in order to keep the value function up to date, unless the strong exponential time hypothesis (SETH) is false; SETH is a widely accepted strengthening of the P $\neq$ NP conjecture. Recall that the number of states in current applications of reinforcement learning is typically astronomical. In contrast, we show that just $\textit{adding}$ a new state-action pair is considerably easier to implement.

Memory Bounds for Continual Learning

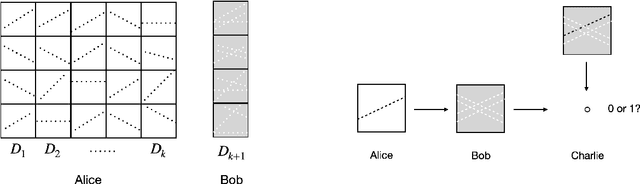
Continual learning, or lifelong learning, is a formidable current challenge to machine learning. It requires the learner to solve a sequence of $k$ different learning tasks, one after the other, while retaining its aptitude for earlier tasks; the continual learner should scale better than the obvious solution of developing and maintaining a separate learner for each of the $k$ tasks. We embark on a complexity-theoretic study of continual learning in the PAC framework. We make novel uses of communication complexity to establish that any continual learner, even an improper one, needs memory that grows linearly with $k$, strongly suggesting that the problem is intractable. When logarithmically many passes over the learning tasks are allowed, we provide an algorithm based on multiplicative weights update whose memory requirement scales well; we also establish that improper learning is necessary for such performance. We conjecture that these results may lead to new promising approaches to continual learning.

Nash, Conley, and Computation: Impossibility and Incompleteness in Game Dynamics

Under what conditions do the behaviors of players, who play a game repeatedly, converge to a Nash equilibrium? If one assumes that the players' behavior is a discrete-time or continuous-time rule whereby the current mixed strategy profile is mapped to the next, this becomes a problem in the theory of dynamical systems. We apply this theory, and in particular the concepts of chain recurrence, attractors, and Conley index, to prove a general impossibility result: there exist games for which any dynamics is bound to have starting points that do not end up at a Nash equilibrium. We also prove a stronger result for $\epsilon$-approximate Nash equilibria: there are games such that no game dynamics can converge (in an appropriate sense) to $\epsilon$-Nash equilibria, and in fact the set of such games has positive measure. Further numerical results demonstrate that this holds for any $\epsilon$ between zero and $0.09$. Our results establish that, although the notions of Nash equilibria (and its computation-inspired approximations) are universally applicable in all games, they are also fundamentally incomplete as predictors of long term behavior, regardless of the choice of dynamics.