Swim till You Sink: Computing the Limit of a Game

During 2023, two interesting results were proven about the limit behavior of game dynamics: First, it was shown that there is a game for which no dynamics converges to the Nash equilibria. Second, it was shown that the sink equilibria of a game adequately capture the limit behavior of natural game dynamics. These two results have created a need and opportunity to articulate a principled computational theory of the meaning of the game that is based on game dynamics. Given any game in normal form, and any prior distribution of play, we study the problem of computing the asymptotic behavior of a class of natural dynamics called the noisy replicator dynamics as a limit distribution over the sink equilibria of the game. When the prior distribution has pure strategy support, we prove this distribution can be computed efficiently, in near-linear time to the size of the best-response graph. When the distribution can be sampled -- for example, if it is the uniform distribution over all mixed strategy profiles -- we show through experiments that the limit distribution of reasonably large games can be estimated quite accurately through sampling and simulation.

The Fairness-Quality Trade-off in Clustering

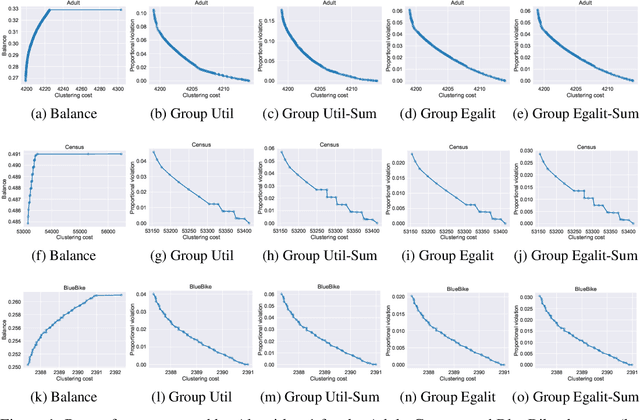
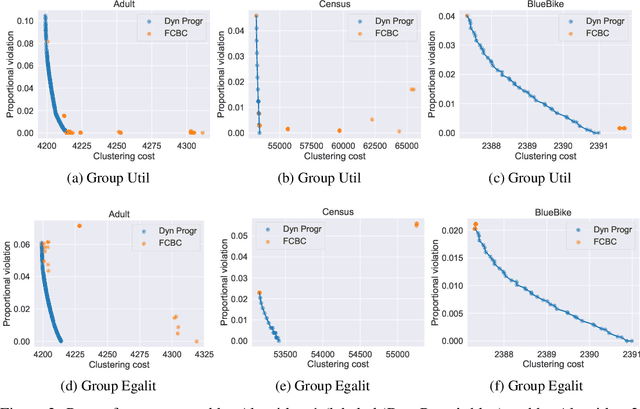
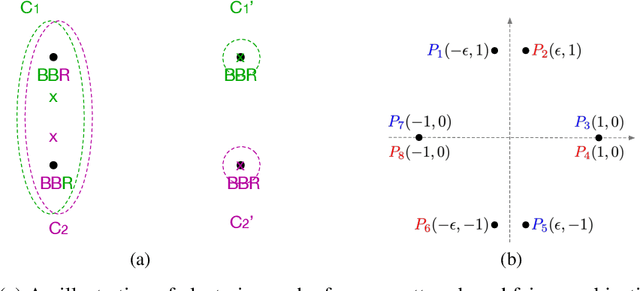
Fairness in clustering has been considered extensively in the past; however, the trade-off between the two objectives -- e.g., can we sacrifice just a little in the quality of the clustering to significantly increase fairness, or vice-versa? -- has rarely been addressed. We introduce novel algorithms for tracing the complete trade-off curve, or Pareto front, between quality and fairness in clustering problems; that is, computing all clusterings that are not dominated in both objectives by other clusterings. Unlike previous work that deals with specific objectives for quality and fairness, we deal with all objectives for fairness and quality in two general classes encompassing most of the special cases addressed in previous work. Our algorithm must take exponential time in the worst case as the Pareto front itself can be exponential. Even when the Pareto front is polynomial, our algorithm may take exponential time, and we prove that this is inevitable unless P = NP. However, we also present a new polynomial-time algorithm for computing the entire Pareto front when the cluster centers are fixed, and for perhaps the most natural fairness objective: minimizing the sum, over all clusters, of the imbalance between the two groups in each cluster.