The Fairness-Quality Trade-off in Clustering

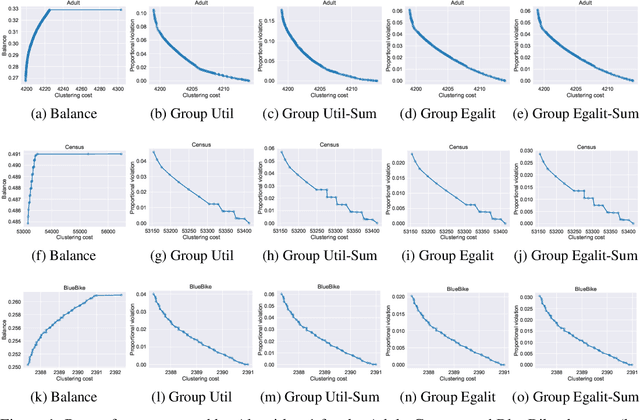
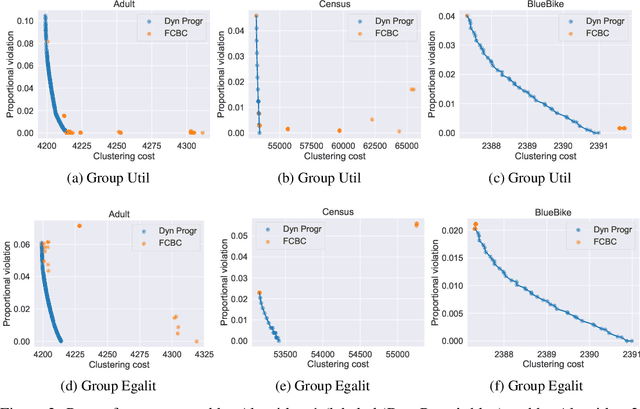
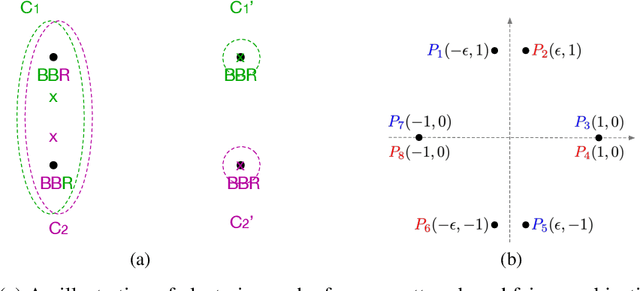
Fairness in clustering has been considered extensively in the past; however, the trade-off between the two objectives -- e.g., can we sacrifice just a little in the quality of the clustering to significantly increase fairness, or vice-versa? -- has rarely been addressed. We introduce novel algorithms for tracing the complete trade-off curve, or Pareto front, between quality and fairness in clustering problems; that is, computing all clusterings that are not dominated in both objectives by other clusterings. Unlike previous work that deals with specific objectives for quality and fairness, we deal with all objectives for fairness and quality in two general classes encompassing most of the special cases addressed in previous work. Our algorithm must take exponential time in the worst case as the Pareto front itself can be exponential. Even when the Pareto front is polynomial, our algorithm may take exponential time, and we prove that this is inevitable unless P = NP. However, we also present a new polynomial-time algorithm for computing the entire Pareto front when the cluster centers are fixed, and for perhaps the most natural fairness objective: minimizing the sum, over all clusters, of the imbalance between the two groups in each cluster.

Center-Embedding and Constituency in the Brain and a New Characterization of Context-Free Languages

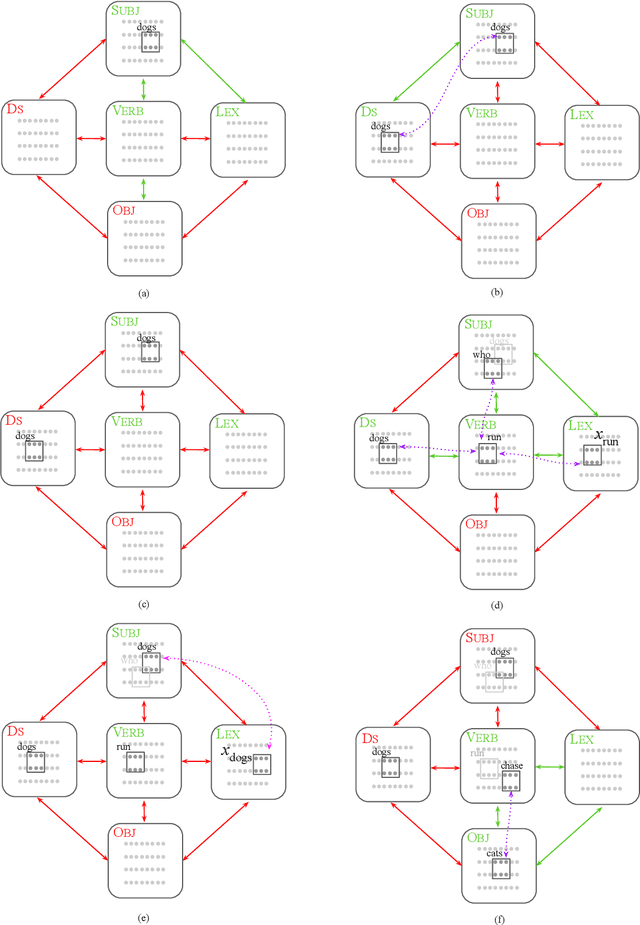
A computational system implemented exclusively through the spiking of neurons was recently shown capable of syntax, that is, of carrying out the dependency parsing of simple English sentences. We address two of the most important questions left open by that work: constituency (the identification of key parts of the sentence such as the verb phrase) and the processing of dependent sentences, especially center-embedded ones. We show that these two aspects of language can also be implemented by neurons and synapses in a way that is compatible with what is known, or widely believed, about the structure and function of the language organ. Surprisingly, the way we implement center embedding points to a new characterization of context-free languages.

The Platform Design Problem

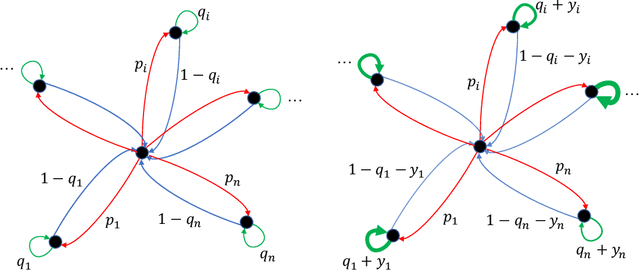
On-line firms deploy suites of software platforms, where each platform is designed to interact with users during a certain activity, such as browsing, chatting, socializing, emailing, driving, etc. The economic and incentive structure of this exchange, as well as its algorithmic nature, have not been explored to our knowledge; we initiate their study in this paper. We model this interaction as a Stackelberg game between a Designer and one or more Agents. We model an Agent as a Markov chain whose states are activities; we assume that the Agent's utility is a linear function of the steady-state distribution of this chain. The Designer may design a platform for each of these activities/states; if a platform is adopted by the Agent, the transition probabilities of the Markov chain are affected, and so is the objective of the Agent. The Designer's utility is a linear function of the steady state probabilities of the accessible states (that is, the ones for which the platform has been adopted), minus the development cost of the platforms. The underlying optimization problem of the Agent -- that is, how to choose the states for which to adopt the platform -- is an MDP. If this MDP has a simple yet plausible structure (the transition probabilities from one state to another only depend on the target state and the recurrent probability of the current state) the Agent's problem can be solved by a greedy algorithm. The Designer's optimization problem (designing a custom suite for the Agent so as to optimize, through the Agent's optimum reaction, the Designer's revenue), while NP-hard, has an FPTAS. These results generalize, under mild additional assumptions, from a single Agent to a distribution of Agents with finite support. The Designer's optimization problem has abysmal "price of robustness", suggesting that learning the parameters of the problem is crucial for the Designer.

Passive Static Equilibrium with Frictional Contacts and Application to Grasp Stability Analysis

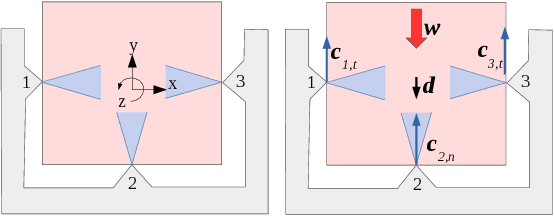
This paper studies the problem of passive grasp stability under an external disturbance, that is, the ability of a grasp to resist a disturbance through passive responses at the contacts. To obtain physically consistent results, such a model must account for friction phenomena at each contact; the difficulty is that friction forces depend in non-linear fashion on contact behavior (stick or slip). We develop the first polynomial-time algorithm which either solves such complex equilibrium constraints for two-dimensional grasps, or otherwise concludes that no solution exists. To achieve this, we show that the number of possible `slip states' (where each contact is labeled as either sticking or slipping) that must be considered is polynomial (in fact quadratic) in the number of contacts, and not exponential as previously thought. Our algorithm captures passive response behaviors at each contact, while accounting for constraints on friction forces such as the maximum dissipation principle.