No-regret learning in harmonic games: Extrapolation in the face of conflicting interests

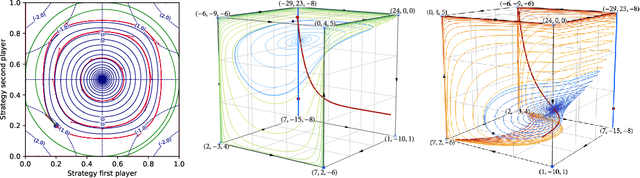
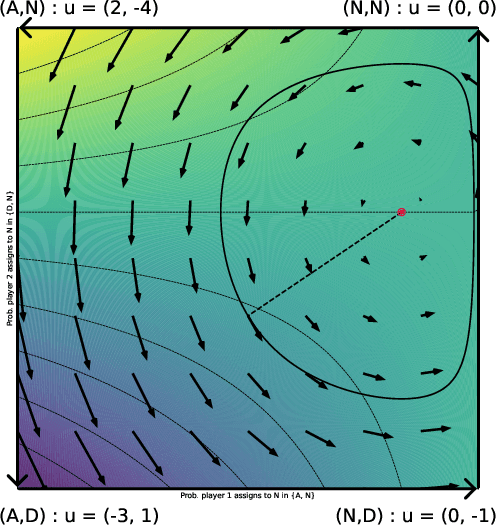
The long-run behavior of multi-agent learning - and, in particular, no-regret learning - is relatively well-understood in potential games, where players have aligned interests. By contrast, in harmonic games - the strategic counterpart of potential games, where players have conflicting interests - very little is known outside the narrow subclass of 2-player zero-sum games with a fully-mixed equilibrium. Our paper seeks to partially fill this gap by focusing on the full class of (generalized) harmonic games and examining the convergence properties of follow-the-regularized-leader (FTRL), the most widely studied class of no-regret learning schemes. As a first result, we show that the continuous-time dynamics of FTRL are Poincar\'e recurrent, that is, they return arbitrarily close to their starting point infinitely often, and hence fail to converge. In discrete time, the standard, "vanilla" implementation of FTRL may lead to even worse outcomes, eventually trapping the players in a perpetual cycle of best-responses. However, if FTRL is augmented with a suitable extrapolation step - which includes as special cases the optimistic and mirror-prox variants of FTRL - we show that learning converges to a Nash equilibrium from any initial condition, and all players are guaranteed at most O(1) regret. These results provide an in-depth understanding of no-regret learning in harmonic games, nesting prior work on 2-player zero-sum games, and showing at a high level that harmonic games are the canonical complement of potential games, not only from a strategic, but also from a dynamic viewpoint.

The Fairness-Quality Trade-off in Clustering

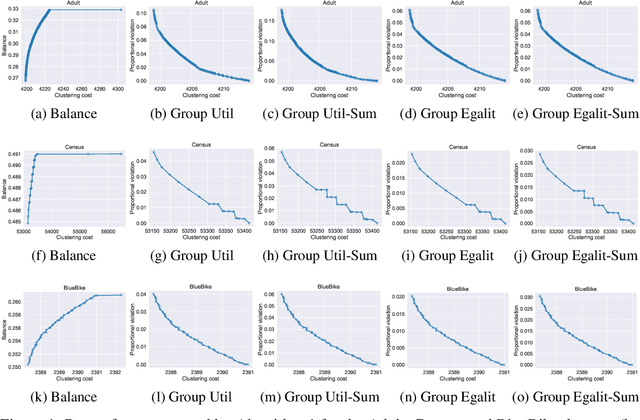
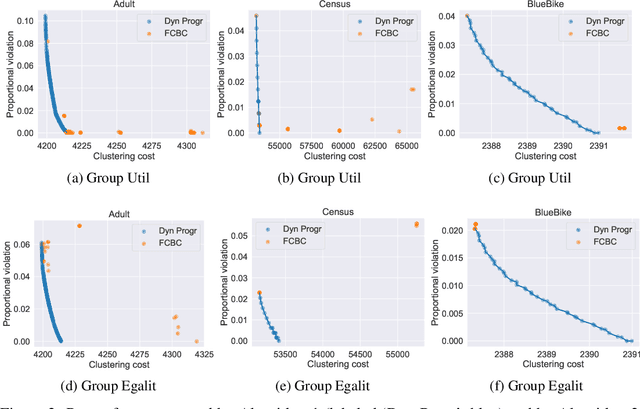
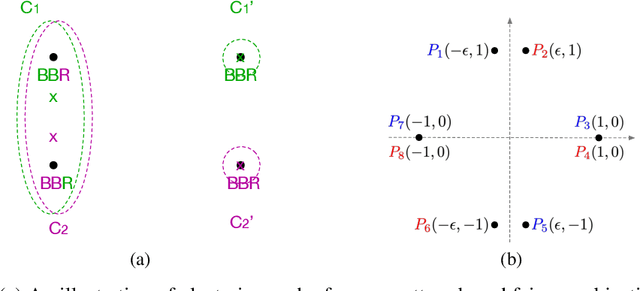
Fairness in clustering has been considered extensively in the past; however, the trade-off between the two objectives -- e.g., can we sacrifice just a little in the quality of the clustering to significantly increase fairness, or vice-versa? -- has rarely been addressed. We introduce novel algorithms for tracing the complete trade-off curve, or Pareto front, between quality and fairness in clustering problems; that is, computing all clusterings that are not dominated in both objectives by other clusterings. Unlike previous work that deals with specific objectives for quality and fairness, we deal with all objectives for fairness and quality in two general classes encompassing most of the special cases addressed in previous work. Our algorithm must take exponential time in the worst case as the Pareto front itself can be exponential. Even when the Pareto front is polynomial, our algorithm may take exponential time, and we prove that this is inevitable unless P = NP. However, we also present a new polynomial-time algorithm for computing the entire Pareto front when the cluster centers are fixed, and for perhaps the most natural fairness objective: minimizing the sum, over all clusters, of the imbalance between the two groups in each cluster.

Coin-Flipping In The Brain: Statistical Learning with Neuronal Assemblies

How intelligence arises from the brain is a central problem in science. A crucial aspect of intelligence is dealing with uncertainty -- developing good predictions about one's environment, and converting these predictions into decisions. The brain itself seems to be noisy at many levels, from chemical processes which drive development and neuronal activity to trial variability of responses to stimuli. One hypothesis is that the noise inherent to the brain's mechanisms is used to sample from a model of the world and generate predictions. To test this hypothesis, we study the emergence of statistical learning in NEMO, a biologically plausible computational model of the brain based on stylized neurons and synapses, plasticity, and inhibition, and giving rise to assemblies -- a group of neurons whose coordinated firing is tantamount to recalling a location, concept, memory, or other primitive item of cognition. We show in theory and simulation that connections between assemblies record statistics, and ambient noise can be harnessed to make probabilistic choices between assemblies. This allows NEMO to create internal models such as Markov chains entirely from the presentation of sequences of stimuli. Our results provide a foundation for biologically plausible probabilistic computation, and add theoretical support to the hypothesis that noise is a useful component of the brain's mechanism for cognition.

The Architecture of a Biologically Plausible Language Organ

We present a simulated biologically plausible language organ, made up of stylized but realistic neurons, synapses, brain areas, plasticity, and a simplified model of sensory perception. We show through experiments that this model succeeds in an important early step in language acquisition: the learning of nouns, verbs, and their meanings, from the grounded input of only a modest number of sentences. Learning in this system is achieved through Hebbian plasticity, and without backpropagation. Our model goes beyond a parser previously designed in a similar environment, with the critical addition of a biologically plausible account for how language can be acquired in the infant's brain, not just processed by a mature brain.

Computation with Sequences in the Brain

Even as machine learning exceeds human-level performance on many applications, the generality, robustness, and rapidity of the brain's learning capabilities remain unmatched. How cognition arises from neural activity is a central open question in neuroscience, inextricable from the study of intelligence itself. A simple formal model of neural activity was proposed in Papadimitriou [2020] and has been subsequently shown, through both mathematical proofs and simulations, to be capable of implementing certain simple cognitive operations via the creation and manipulation of assemblies of neurons. However, many intelligent behaviors rely on the ability to recognize, store, and manipulate temporal sequences of stimuli (planning, language, navigation, to list a few). Here we show that, in the same model, time can be captured naturally as precedence through synaptic weights and plasticity, and, as a result, a range of computations on sequences of assemblies can be carried out. In particular, repeated presentation of a sequence of stimuli leads to the memorization of the sequence through corresponding neural assemblies: upon future presentation of any stimulus in the sequence, the corresponding assembly and its subsequent ones will be activated, one after the other, until the end of the sequence. Finally, we show that any finite state machine can be learned in a similar way, through the presentation of appropriate patterns of sequences. Through an extension of this mechanism, the model can be shown to be capable of universal computation. We support our analysis with a number of experiments to probe the limits of learning in this model in key ways. Taken together, these results provide a concrete hypothesis for the basis of the brain's remarkable abilities to compute and learn, with sequences playing a vital role.

Center-Embedding and Constituency in the Brain and a New Characterization of Context-Free Languages

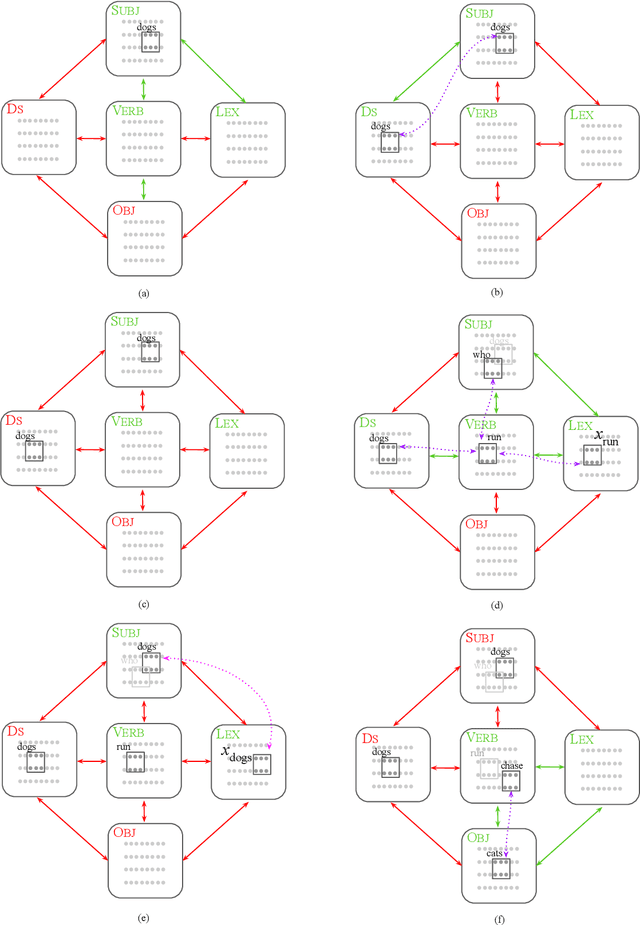
A computational system implemented exclusively through the spiking of neurons was recently shown capable of syntax, that is, of carrying out the dependency parsing of simple English sentences. We address two of the most important questions left open by that work: constituency (the identification of key parts of the sentence such as the verb phrase) and the processing of dependent sentences, especially center-embedded ones. We show that these two aspects of language can also be implemented by neurons and synapses in a way that is compatible with what is known, or widely believed, about the structure and function of the language organ. Surprisingly, the way we implement center embedding points to a new characterization of context-free languages.

Planning with Biological Neurons and Synapses

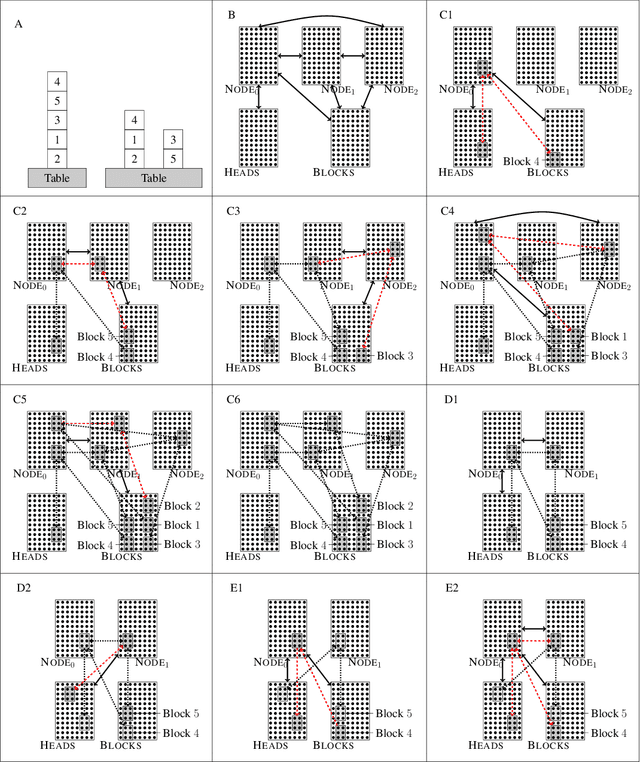
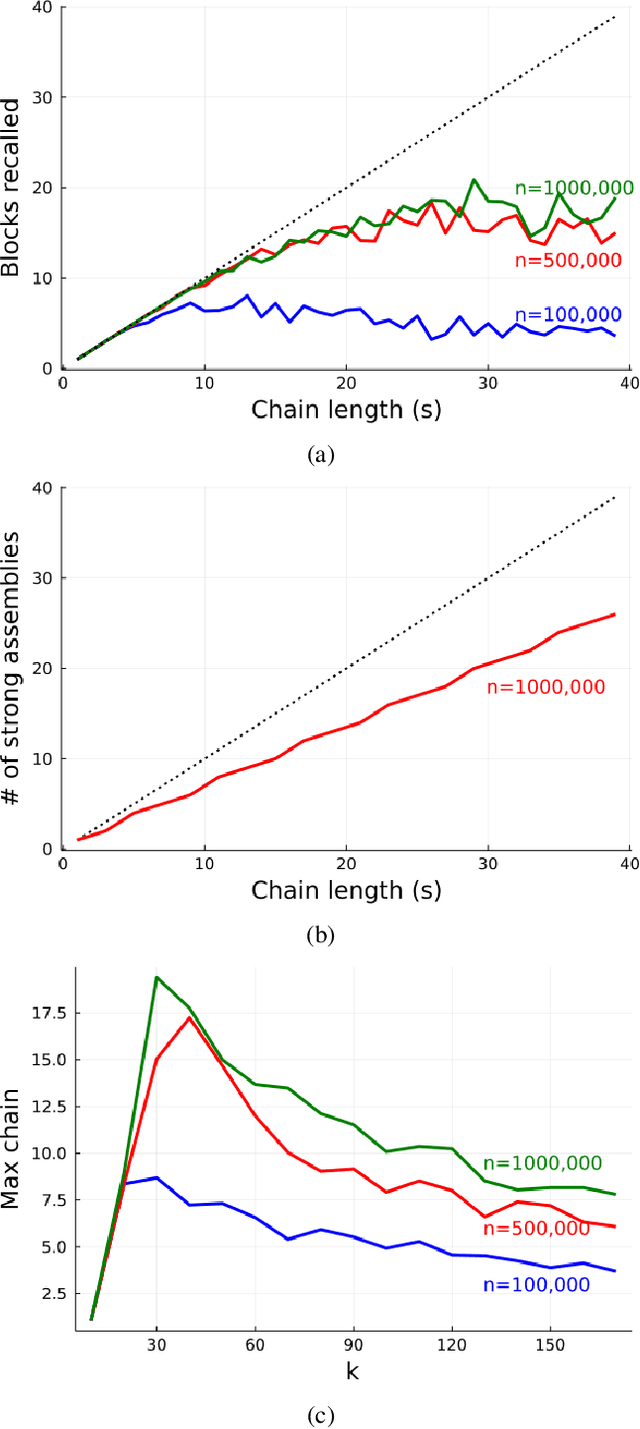
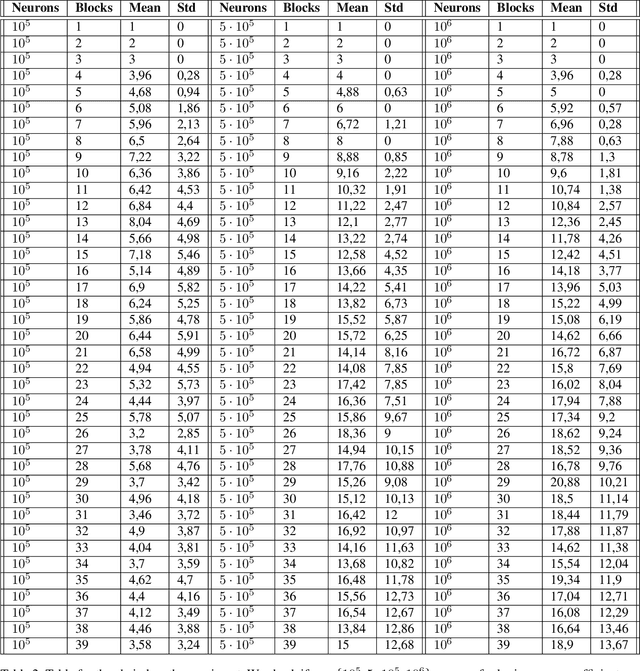
We revisit the planning problem in the blocks world, and we implement a known heuristic for this task. Importantly, our implementation is biologically plausible, in the sense that it is carried out exclusively through the spiking of neurons. Even though much has been accomplished in the blocks world over the past five decades, we believe that this is the first algorithm of its kind. The input is a sequence of symbols encoding an initial set of block stacks as well as a target set, and the output is a sequence of motion commands such as "put the top block in stack 1 on the table". The program is written in the Assembly Calculus, a recently proposed computational framework meant to model computation in the brain by bridging the gap between neural activity and cognitive function. Its elementary objects are assemblies of neurons (stable sets of neurons whose simultaneous firing signifies that the subject is thinking of an object, concept, word, etc.), its commands include project and merge, and its execution model is based on widely accepted tenets of neuroscience. A program in this framework essentially sets up a dynamical system of neurons and synapses that eventually, with high probability, accomplishes the task. The purpose of this work is to establish empirically that reasonably large programs in the Assembly Calculus can execute correctly and reliably; and that rather realistic -- if idealized -- higher cognitive functions, such as planning in the blocks world, can be implemented successfully by such programs.

Assemblies of neurons can learn to classify well-separated distributions

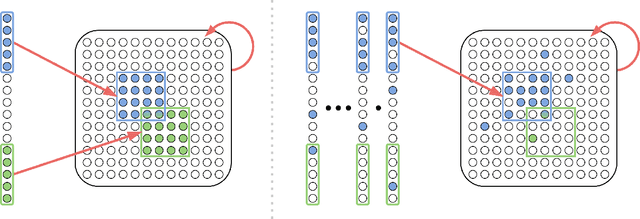
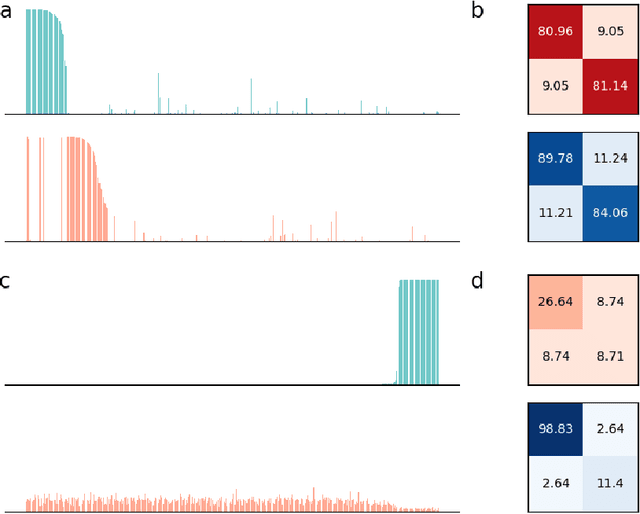
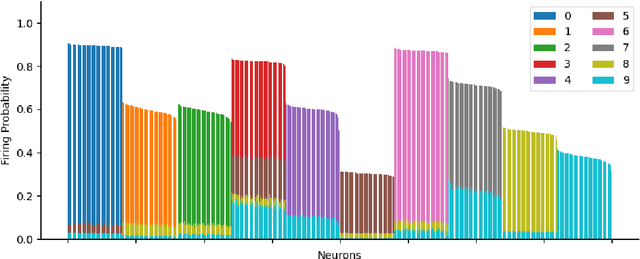
Assemblies are patterns of coordinated firing across large populations of neurons, believed to represent higher-level information in the brain, such as memories, concepts, words, and other cognitive categories. Recently, a computational system called the Assembly Calculus (AC) has been proposed, based on a set of biologically plausible operations on assemblies. This system is capable of simulating arbitrary space-bounded computation, and describes quite naturally complex cognitive phenomena such as language. However, the question of whether assemblies can perform the brain's greatest trick -- its ability to learn -- has been open. We show that the AC provides a mechanism for learning to classify samples from well-separated classes. We prove rigorously that for simple classification problems, a new assembly that represents each class can be reliably formed in response to a few stimuli from it; this assembly is henceforth reliably recalled in response to new stimuli from the same class. Furthermore, such class assemblies will be distinguishable as long as the respective classes are reasonably separated, in particular when they are clusters of similar assemblies, or more generally divided by a halfspace with margin. Experimentally, we demonstrate the successful formation of assemblies which represent concept classes on synthetic data drawn from these distributions, and also on MNIST, which lends itself to classification through one assembly per digit. Seen as a learning algorithm, this mechanism is entirely online, generalizes from very few samples, and requires only mild supervision -- all key attributes of learning in a model of the brain.

A Biologically Plausible Parser

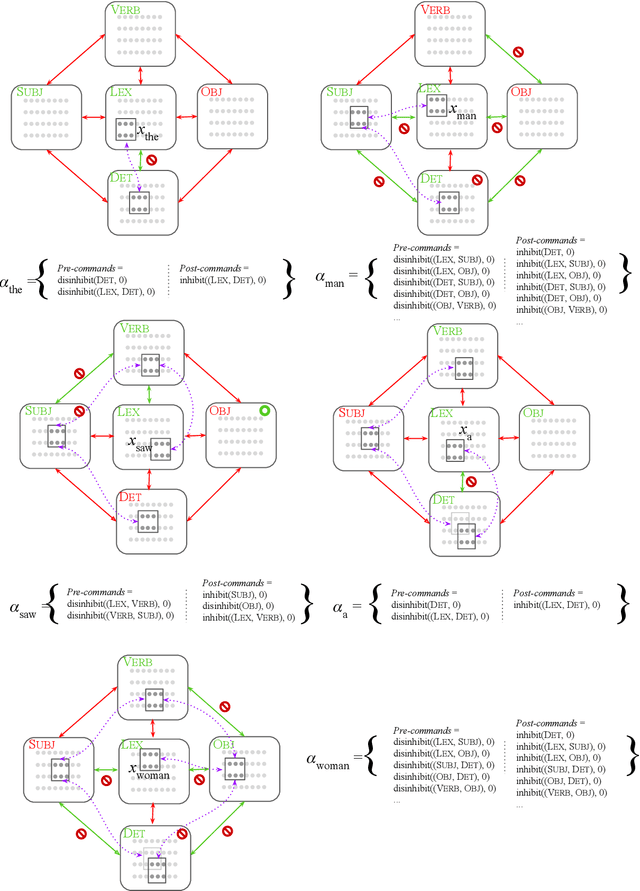
We describe a parser of English effectuated by biologically plausible neurons and synapses, and implemented through the Assembly Calculus, a recently proposed computational framework for cognitive function. We demonstrate that this device is capable of correctly parsing reasonably nontrivial sentences. While our experiments entail rather simple sentences in English, our results suggest that the parser can be extended beyond what we have implemented, to several directions encompassing much of language. For example, we present a simple Russian version of the parser, and discuss how to handle recursion, embedding, and polysemy.

Smoothed Analysis of Discrete Tensor Decomposition and Assemblies of Neurons

We analyze linear independence of rank one tensors produced by tensor powers of randomly perturbed vectors. This enables efficient decomposition of sums of high-order tensors. Our analysis builds upon [BCMV14] but allows for a wider range of perturbation models, including discrete ones. We give an application to recovering assemblies of neurons. Assemblies are large sets of neurons representing specific memories or concepts. The size of the intersection of two assemblies has been shown in experiments to represent the extent to which these memories co-occur or these concepts are related; the phenomenon is called association of assemblies. This suggests that an animal's memory is a complex web of associations, and poses the problem of recovering this representation from cognitive data. Motivated by this problem, we study the following more general question: Can we reconstruct the Venn diagram of a family of sets, given the sizes of their $\ell$-wise intersections? We show that as long as the family of sets is randomly perturbed, it is enough for the number of measurements to be polynomially larger than the number of nonempty regions of the Venn diagram to fully reconstruct the diagram.