Sample Efficient Omniprediction and Downstream Swap Regret for Non-Linear Losses

We define "decision swap regret" which generalizes both prediction for downstream swap regret and omniprediction, and give algorithms for obtaining it for arbitrary multi-dimensional Lipschitz loss functions in online adversarial settings. We also give sample complexity bounds in the batch setting via an online-to-batch reduction. When applied to omniprediction, our algorithm gives the first polynomial sample-complexity bounds for Lipschitz loss functions -- prior bounds either applied only to linear loss (or binary outcomes) or scaled exponentially with the error parameter even under the assumption that the loss functions were convex. When applied to prediction for downstream regret, we give the first algorithm capable of guaranteeing swap regret bounds for all downstream agents with non-linear loss functions over a multi-dimensional outcome space: prior work applied only to linear loss functions, modeling risk neutral agents. Our general bounds scale exponentially with the dimension of the outcome space, but we give improved regret and sample complexity bounds for specific families of multidimensional functions of economic interest: constant elasticity of substitution (CES), Cobb-Douglas, and Leontief utility functions.

Algorithmic Aspects of Strategic Trading

Algorithmic trading in modern financial markets is widely acknowledged to exhibit strategic, game-theoretic behaviors whose complexity can be difficult to model. A recent series of papers (Chriss, 2024b,c,a, 2025) has made progress in the setting of trading for position building. Here parties wish to buy or sell a fixed number of shares in a fixed time period in the presence of both temporary and permanent market impact, resulting in exponentially large strategy spaces. While these papers primarily consider the existence and structural properties of equilibrium strategies, in this work we focus on the algorithmic aspects of the proposed model. We give an efficient algorithm for computing best responses, and show that while the temporary impact only setting yields a potential game, best response dynamics do not generally converge for the general setting, for which no fast algorithm for (Nash) equilibrium computation is known. This leads us to consider the broader notion of Coarse Correlated Equilibria (CCE), which we show can be computed efficiently via an implementation of Follow the Perturbed Leader (FTPL). We illustrate the model and our results with an experimental investigation, where FTPL exhibits interesting behavior in different regimes of the relative weighting between temporary and permanent market impact.

An Elementary Predictor Obtaining $2\sqrt{T}$ Distance to Calibration

Blasiok et al. [2023] proposed distance to calibration as a natural measure of calibration error that unlike expected calibration error (ECE) is continuous. Recently, Qiao and Zheng [2024] gave a non-constructive argument establishing the existence of an online predictor that can obtain $O(\sqrt{T})$ distance to calibration in the adversarial setting, which is known to be impossible for ECE. They leave as an open problem finding an explicit, efficient algorithm. We resolve this problem and give an extremely simple, efficient, deterministic algorithm that obtains distance to calibration error at most $2\sqrt{T}$.

Forecasting for Swap Regret for All Downstream Agents

We study the problem of making predictions so that downstream agents who best respond to them will be guaranteed diminishing swap regret, no matter what their utility functions are. It has been known since Foster and Vohra (1997) that agents who best-respond to calibrated forecasts have no swap regret. Unfortunately, the best known algorithms for guaranteeing calibrated forecasts in sequential adversarial environments do so at rates that degrade exponentially with the dimension of the prediction space. In this work, we show that by making predictions that are not calibrated, but are unbiased subject to a carefully selected collection of events, we can guarantee arbitrary downstream agents diminishing swap regret at rates that substantially improve over the rates that result from calibrated forecasts -- while maintaining the appealing property that our forecasts give guarantees for any downstream agent, without our forecasting algorithm needing to know their utility function. We give separate results in the ``low'' (1 or 2) dimensional setting and the ``high'' ($> 2$) dimensional setting. In the low dimensional setting, we show how to make predictions such that all agents who best respond to our predictions have diminishing swap regret -- in 1 dimension, at the optimal $O(\sqrt{T})$ rate. In the high dimensional setting we show how to make forecasts that guarantee regret scaling at a rate of $O(T^{2/3})$ (crucially, a dimension independent exponent), under the assumption that downstream agents smoothly best respond. Our results stand in contrast to rates that derive from agents who best respond to calibrated forecasts, which have an exponential dependence on the dimension of the prediction space.

Center-Embedding and Constituency in the Brain and a New Characterization of Context-Free Languages

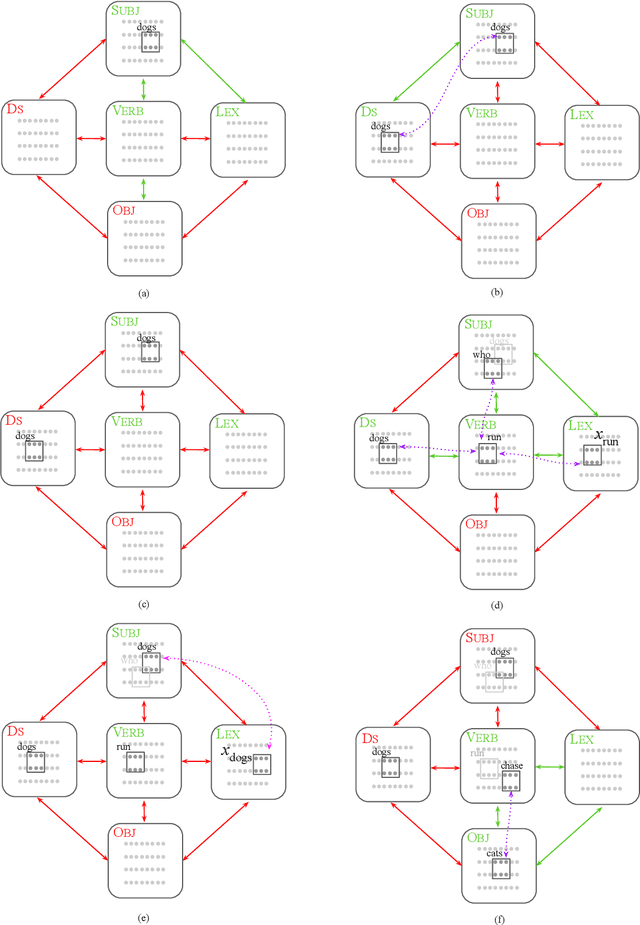
A computational system implemented exclusively through the spiking of neurons was recently shown capable of syntax, that is, of carrying out the dependency parsing of simple English sentences. We address two of the most important questions left open by that work: constituency (the identification of key parts of the sentence such as the verb phrase) and the processing of dependent sentences, especially center-embedded ones. We show that these two aspects of language can also be implemented by neurons and synapses in a way that is compatible with what is known, or widely believed, about the structure and function of the language organ. Surprisingly, the way we implement center embedding points to a new characterization of context-free languages.