Algorithmic Collusion Without Threats

There has been substantial recent concern that pricing algorithms might learn to ``collude.'' Supra-competitive prices can emerge as a Nash equilibrium of repeated pricing games, in which sellers play strategies which threaten to punish their competitors who refuse to support high prices, and these strategies can be automatically learned. In fact, a standard economic intuition is that supra-competitive prices emerge from either the use of threats, or a failure of one party to optimize their payoff. Is this intuition correct? Would preventing threats in algorithmic decision-making prevent supra-competitive prices when sellers are optimizing for their own revenue? No. We show that supra-competitive prices can emerge even when both players are using algorithms which do not encode threats, and which optimize for their own revenue. We study sequential pricing games in which a first mover deploys an algorithm and then a second mover optimizes within the resulting environment. We show that if the first mover deploys any algorithm with a no-regret guarantee, and then the second mover even approximately optimizes within this now static environment, monopoly-like prices arise. The result holds for any no-regret learning algorithm deployed by the first mover and for any pricing policy of the second mover that obtains them profit at least as high as a random pricing would -- and hence the result applies even when the second mover is optimizing only within a space of non-responsive pricing distributions which are incapable of encoding threats. In fact, there exists a set of strategies, neither of which explicitly encode threats that form a Nash equilibrium of the simultaneous pricing game in algorithm space, and lead to near monopoly prices. This suggests that the definition of ``algorithmic collusion'' may need to be expanded, to include strategies without explicitly encoded threats.

An Elementary Predictor Obtaining $2\sqrt{T}$ Distance to Calibration

Blasiok et al. [2023] proposed distance to calibration as a natural measure of calibration error that unlike expected calibration error (ECE) is continuous. Recently, Qiao and Zheng [2024] gave a non-constructive argument establishing the existence of an online predictor that can obtain $O(\sqrt{T})$ distance to calibration in the adversarial setting, which is known to be impossible for ECE. They leave as an open problem finding an explicit, efficient algorithm. We resolve this problem and give an extremely simple, efficient, deterministic algorithm that obtains distance to calibration error at most $2\sqrt{T}$.

Oracle Efficient Algorithms for Groupwise Regret

We study the problem of online prediction, in which at each time step $t$, an individual $x_t$ arrives, whose label we must predict. Each individual is associated with various groups, defined based on their features such as age, sex, race etc., which may intersect. Our goal is to make predictions that have regret guarantees not just overall but also simultaneously on each sub-sequence comprised of the members of any single group. Previous work such as [Blum & Lykouris] and [Lee et al] provide attractive regret guarantees for these problems; however, these are computationally intractable on large model classes. We show that a simple modification of the sleeping experts technique of [Blum & Lykouris] yields an efficient reduction to the well-understood problem of obtaining diminishing external regret absent group considerations. Our approach gives similar regret guarantees compared to [Blum & Lykouris]; however, we run in time linear in the number of groups, and are oracle-efficient in the hypothesis class. This in particular implies that our algorithm is efficient whenever the number of groups is polynomially bounded and the external-regret problem can be solved efficiently, an improvement on [Blum & Lykouris]'s stronger condition that the model class must be small. Our approach can handle online linear regression and online combinatorial optimization problems like online shortest paths. Beyond providing theoretical regret bounds, we evaluate this algorithm with an extensive set of experiments on synthetic data and on two real data sets -- Medical costs and the Adult income dataset, both instantiated with intersecting groups defined in terms of race, sex, and other demographic characteristics. We find that uniformly across groups, our algorithm gives substantial error improvements compared to running a standard online linear regression algorithm with no groupwise regret guarantees.

Pipeline Interventions

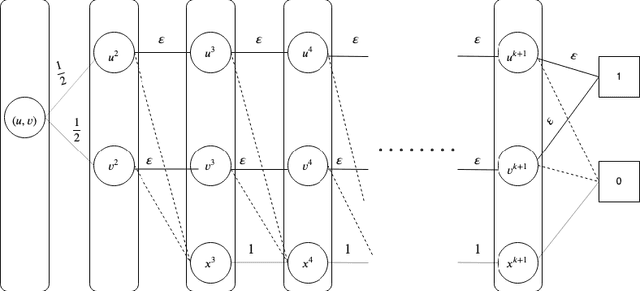
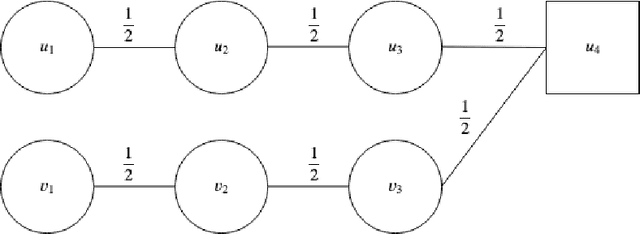
We introduce the \emph{pipeline intervention} problem, defined by a layered directed acyclic graph and a set of stochastic matrices governing transitions between successive layers. The graph is a stylized model for how people from different populations are presented opportunities, eventually leading to some reward. In our model, individuals are born into an initial position (i.e. some node in the first layer of the graph) according to a fixed probability distribution, and then stochastically progress through the graph according to the transition matrices, until they reach a node in the final layer of the graph; each node in the final layer has a \emph{reward} associated with it. The pipeline intervention problem asks how to best make costly changes to the transition matrices governing people's stochastic transitions through the graph, subject to a budget constraint. We consider two objectives: social welfare maximization, and a fairness-motivated maximin objective that seeks to maximize the value to the population (starting node) with the \emph{least} expected value. We consider two variants of the maximin objective that turn out to be distinct, depending on whether we demand a deterministic solution or allow randomization. For each objective, we give an efficient approximation algorithm (an additive FPTAS) for constant width networks. We also tightly characterize the "price of fairness" in our setting: the ratio between the highest achievable social welfare and the highest social welfare consistent with a maximin optimal solution. Finally we show that for polynomial width networks, even approximating the maximin objective to any constant factor is NP hard, even for networks with constant depth. This shows that the restriction on the width in our positive results is essential.