Multi-Agent Performative Prediction Beyond the Insensitivity Assumption: A Case Study for Mortgage Competition

Performative prediction models account for feedback loops in decision-making processes where predictions influence future data distributions. While existing work largely assumes insensitivity of data distributions to small strategy changes, this assumption usually fails in real-world competitive (i.e. multi-agent) settings. For example, in Bertrand-type competitions, a small reduction in one firm's price can lead that firm to capture the entire demand, while all others sharply lose all of their customers. We study a representative setting of multi-agent performative prediction in which insensitivity assumptions do not hold, and investigate the convergence of natural dynamics. To do so, we focus on a specific game that we call the ''Bank Game'', where two lenders compete over interest rates and credit score thresholds. Consumers act similarly as to in a Bertrand Competition, with each consumer selecting the firm with the lowest interest rate that they are eligible for based on the firms' credit thresholds. Our analysis characterizes the equilibria of this game and demonstrates that when both firms use a common and natural no-regret learning dynamic -- exponential weights -- with proper initialization, the dynamics always converge to stable outcomes despite the general-sum structure. Notably, our setting admits multiple stable equilibria, with convergence dependent on initial conditions. We also provide theoretical convergence results in the stochastic case when the utility matrix is not fully known, but each learner can observe sufficiently many samples of consumers at each time step to estimate it, showing robustness to slight mis-specifications. Finally, we provide experimental results that validate our theoretical findings.

Improving Minimax Group Fairness in Sequential Recommendation

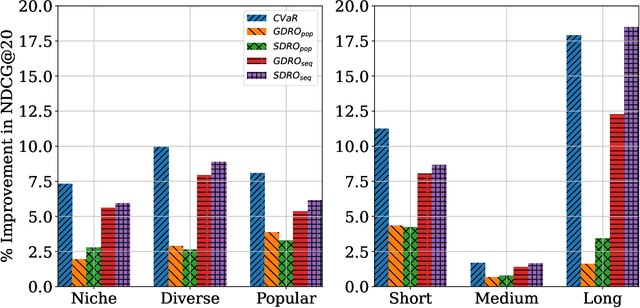
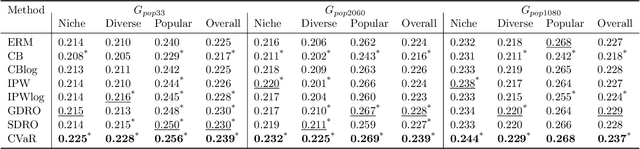
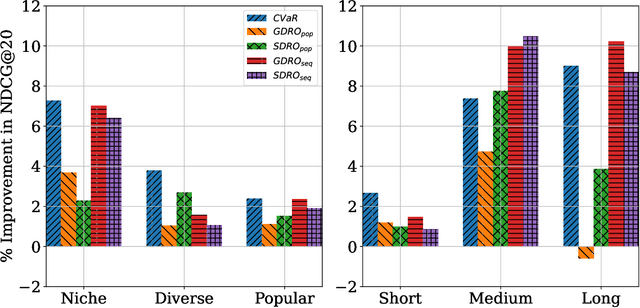
Training sequential recommenders such as SASRec with uniform sample weights achieves good overall performance but can fall short on specific user groups. One such example is popularity bias, where mainstream users receive better recommendations than niche content viewers. To improve recommendation quality across diverse user groups, we explore three Distributionally Robust Optimization(DRO) methods: Group DRO, Streaming DRO, and Conditional Value at Risk (CVaR) DRO. While Group and Streaming DRO rely on group annotations and struggle with users belonging to multiple groups, CVaR does not require such annotations and can naturally handle overlapping groups. In experiments on two real-world datasets, we show that the DRO methods outperform standard training, with CVaR delivering the best results. Additionally, we find that Group and Streaming DRO are sensitive to the choice of group used for loss computation. Our contributions include (i) a novel application of CVaR to recommenders, (ii) showing that the DRO methods improve group metrics as well as overall performance, and (iii) demonstrating CVaR's effectiveness in the practical scenario of intersecting user groups.

Personalized Differential Privacy for Ridge Regression

The increased application of machine learning (ML) in sensitive domains requires protecting the training data through privacy frameworks, such as differential privacy (DP). DP requires to specify a uniform privacy level $\varepsilon$ that expresses the maximum privacy loss that each data point in the entire dataset is willing to tolerate. Yet, in practice, different data points often have different privacy requirements. Having to set one uniform privacy level is usually too restrictive, often forcing a learner to guarantee the stringent privacy requirement, at a large cost to accuracy. To overcome this limitation, we introduce our novel Personalized-DP Output Perturbation method (PDP-OP) that enables to train Ridge regression models with individual per data point privacy levels. We provide rigorous privacy proofs for our PDP-OP as well as accuracy guarantees for the resulting model. This work is the first to provide such theoretical accuracy guarantees when it comes to personalized DP in machine learning, whereas previous work only provided empirical evaluations. We empirically evaluate PDP-OP on synthetic and real datasets and with diverse privacy distributions. We show that by enabling each data point to specify their own privacy requirement, we can significantly improve the privacy-accuracy trade-offs in DP. We also show that PDP-OP outperforms the personalized privacy techniques of Jorgensen et al. (2015).

Oracle Efficient Algorithms for Groupwise Regret

We study the problem of online prediction, in which at each time step $t$, an individual $x_t$ arrives, whose label we must predict. Each individual is associated with various groups, defined based on their features such as age, sex, race etc., which may intersect. Our goal is to make predictions that have regret guarantees not just overall but also simultaneously on each sub-sequence comprised of the members of any single group. Previous work such as [Blum & Lykouris] and [Lee et al] provide attractive regret guarantees for these problems; however, these are computationally intractable on large model classes. We show that a simple modification of the sleeping experts technique of [Blum & Lykouris] yields an efficient reduction to the well-understood problem of obtaining diminishing external regret absent group considerations. Our approach gives similar regret guarantees compared to [Blum & Lykouris]; however, we run in time linear in the number of groups, and are oracle-efficient in the hypothesis class. This in particular implies that our algorithm is efficient whenever the number of groups is polynomially bounded and the external-regret problem can be solved efficiently, an improvement on [Blum & Lykouris]'s stronger condition that the model class must be small. Our approach can handle online linear regression and online combinatorial optimization problems like online shortest paths. Beyond providing theoretical regret bounds, we evaluate this algorithm with an extensive set of experiments on synthetic data and on two real data sets -- Medical costs and the Adult income dataset, both instantiated with intersecting groups defined in terms of race, sex, and other demographic characteristics. We find that uniformly across groups, our algorithm gives substantial error improvements compared to running a standard online linear regression algorithm with no groupwise regret guarantees.