Model Ensembling for Constrained Optimization

There is a long history in machine learning of model ensembling, beginning with boosting and bagging and continuing to the present day. Much of this history has focused on combining models for classification and regression, but recently there is interest in more complex settings such as ensembling policies in reinforcement learning. Strong connections have also emerged between ensembling and multicalibration techniques. In this work, we further investigate these themes by considering a setting in which we wish to ensemble models for multidimensional output predictions that are in turn used for downstream optimization. More precisely, we imagine we are given a number of models mapping a state space to multidimensional real-valued predictions. These predictions form the coefficients of a linear objective that we would like to optimize under specified constraints. The fundamental question we address is how to improve and combine such models in a way that outperforms the best of them in the downstream optimization problem. We apply multicalibration techniques that lead to two provably efficient and convergent algorithms. The first of these (the white box approach) requires being given models that map states to output predictions, while the second (the \emph{black box} approach) requires only policies (mappings from states to solutions to the optimization problem). For both, we provide convergence and utility guarantees. We conclude by investigating the performance and behavior of the two algorithms in a controlled experimental setting.

Diversified Ensembling: An Experiment in Crowdsourced Machine Learning

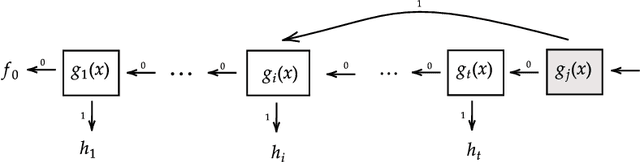
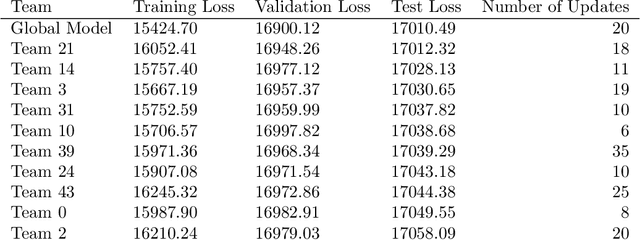
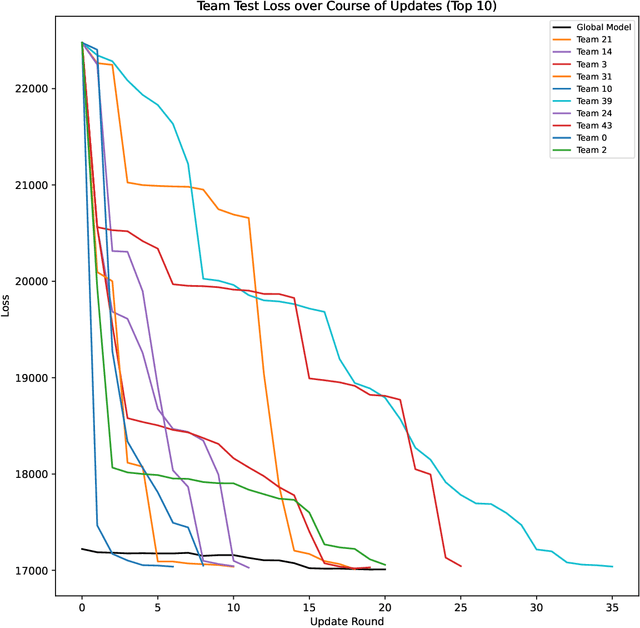
Crowdsourced machine learning on competition platforms such as Kaggle is a popular and often effective method for generating accurate models. Typically, teams vie for the most accurate model, as measured by overall error on a holdout set, and it is common towards the end of such competitions for teams at the top of the leaderboard to ensemble or average their models outside the platform mechanism to get the final, best global model. In arXiv:2201.10408, the authors developed an alternative crowdsourcing framework in the context of fair machine learning, in order to integrate community feedback into models when subgroup unfairness is present and identifiable. There, unlike in classical crowdsourced ML, participants deliberately specialize their efforts by working on subproblems, such as demographic subgroups in the service of fairness. Here, we take a broader perspective on this work: we note that within this framework, participants may both specialize in the service of fairness and simply to cater to their particular expertise (e.g., focusing on identifying bird species in an image classification task). Unlike traditional crowdsourcing, this allows for the diversification of participants' efforts and may provide a participation mechanism to a larger range of individuals (e.g. a machine learning novice who has insight into a specific fairness concern). We present the first medium-scale experimental evaluation of this framework, with 46 participating teams attempting to generate models to predict income from American Community Survey data. We provide an empirical analysis of teams' approaches, and discuss the novel system architecture we developed. From here, we give concrete guidance for how best to deploy such a framework.

Multicalibration as Boosting for Regression

We study the connection between multicalibration and boosting for squared error regression. First we prove a useful characterization of multicalibration in terms of a ``swap regret'' like condition on squared error. Using this characterization, we give an exceedingly simple algorithm that can be analyzed both as a boosting algorithm for regression and as a multicalibration algorithm for a class H that makes use only of a standard squared error regression oracle for H. We give a weak learning assumption on H that ensures convergence to Bayes optimality without the need to make any realizability assumptions -- giving us an agnostic boosting algorithm for regression. We then show that our weak learning assumption on H is both necessary and sufficient for multicalibration with respect to H to imply Bayes optimality. We also show that if H satisfies our weak learning condition relative to another class C then multicalibration with respect to H implies multicalibration with respect to C. Finally we investigate the empirical performance of our algorithm experimentally using an open source implementation that we make available. Our code repository can be found at https://github.com/Declancharrison/Level-Set-Boosting.

Multicalibrated Regression for Downstream Fairness

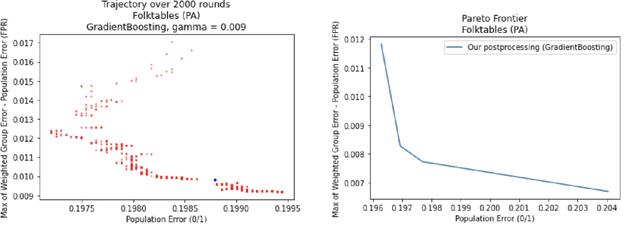
We show how to take a regression function $\hat{f}$ that is appropriately ``multicalibrated'' and efficiently post-process it into an approximately error minimizing classifier satisfying a large variety of fairness constraints. The post-processing requires no labeled data, and only a modest amount of unlabeled data and computation. The computational and sample complexity requirements of computing $\hat f$ are comparable to the requirements for solving a single fair learning task optimally, but it can in fact be used to solve many different downstream fairness-constrained learning problems efficiently. Our post-processing method easily handles intersecting groups, generalizing prior work on post-processing regression functions to satisfy fairness constraints that only applied to disjoint groups. Our work extends recent work showing that multicalibrated regression functions are ``omnipredictors'' (i.e. can be post-processed to optimally solve unconstrained ERM problems) to constrained optimization.

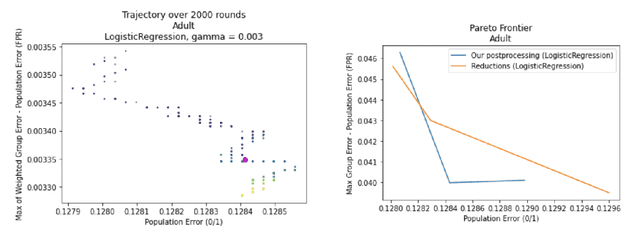
Beyond the Frontier: Fairness Without Accuracy Loss

Notions of fair machine learning that seek to control various kinds of error across protected groups generally are cast as constrained optimization problems over a fixed model class. For such problems, tradeoffs arise: asking for various kinds of technical fairness requires compromising on overall error, and adding more protected groups increases error rates across all groups. Our goal is to break though such accuracy-fairness tradeoffs. We develop a simple algorithmic framework that allows us to deploy models and then revise them dynamically when groups are discovered on which the error rate is suboptimal. Protected groups don't need to be pre-specified: At any point, if it is discovered that there is some group on which our current model performs substantially worse than optimally, then there is a simple update operation that improves the error on that group without increasing either overall error or the error on previously identified groups. We do not restrict the complexity of the groups that can be identified, and they can intersect in arbitrary ways. The key insight that allows us to break through the tradeoff barrier is to dynamically expand the model class as new groups are identified. The result is provably fast convergence to a model that can't be distinguished from the Bayes optimal predictor, at least by those tasked with finding high error groups. We explore two instantiations of this framework: as a "bias bug bounty" design in which external auditors are invited to discover groups on which our current model's error is suboptimal, and as an algorithmic paradigm in which the discovery of groups on which the error is suboptimal is posed as an optimization problem. In the bias bounty case, when we say that a model cannot be distinguished from Bayes optimal, we mean by any participant in the bounty program. We provide both theoretical analysis and experimental validation.

Non-parametric Differentially Private Confidence Intervals for the Median

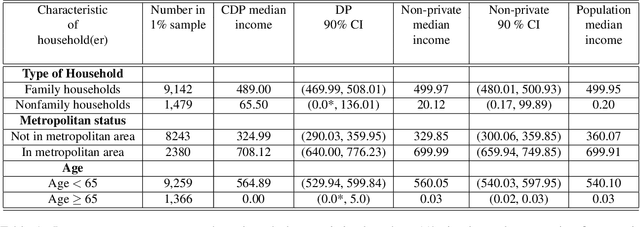
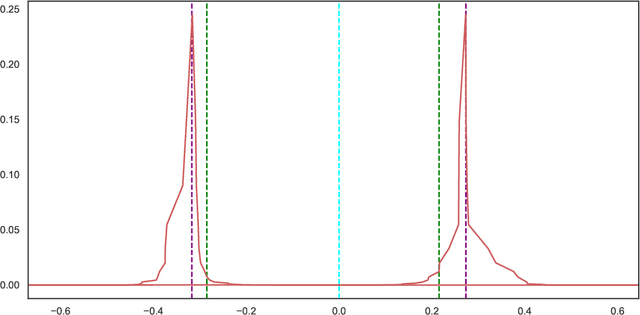
Differential privacy is a restriction on data processing algorithms that provides strong confidentiality guarantees for individual records in the data. However, research on proper statistical inference, that is, research on properly quantifying the uncertainty of the (noisy) sample estimate regarding the true value in the population, is currently still limited. This paper proposes and evaluates several strategies to compute valid differentially private confidence intervals for the median. Instead of computing a differentially private point estimate and deriving its uncertainty, we directly estimate the interval bounds and discuss why this approach is superior if ensuring privacy is important. We also illustrate that addressing both sources of uncertainty--the error from sampling and the error from protecting the output--simultaneously should be preferred over simpler approaches that incorporate the uncertainty in a sequential fashion. We evaluate the performance of the different algorithms under various parameter settings in extensive simulation studies and demonstrate how the findings could be applied in practical settings using data from the 1940 Decennial Census.

Lexicographically Fair Learning: Algorithms and Generalization

We extend the notion of minimax fairness in supervised learning problems to its natural conclusion: lexicographic minimax fairness (or lexifairness for short). Informally, given a collection of demographic groups of interest, minimax fairness asks that the error of the group with the highest error be minimized. Lexifairness goes further and asks that amongst all minimax fair solutions, the error of the group with the second highest error should be minimized, and amongst all of those solutions, the error of the group with the third highest error should be minimized, and so on. Despite its naturalness, correctly defining lexifairness is considerably more subtle than minimax fairness, because of inherent sensitivity to approximation error. We give a notion of approximate lexifairness that avoids this issue, and then derive oracle-efficient algorithms for finding approximately lexifair solutions in a very general setting. When the underlying empirical risk minimization problem absent fairness constraints is convex (as it is, for example, with linear and logistic regression), our algorithms are provably efficient even in the worst case. Finally, we show generalization bounds -- approximate lexifairness on the training sample implies approximate lexifairness on the true distribution with high probability. Our ability to prove generalization bounds depends on our choosing definitions that avoid the instability of naive definitions.

Improved Differentially Private Analysis of Variance

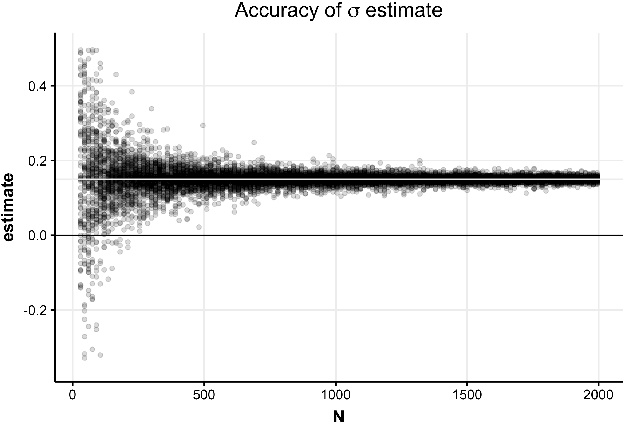
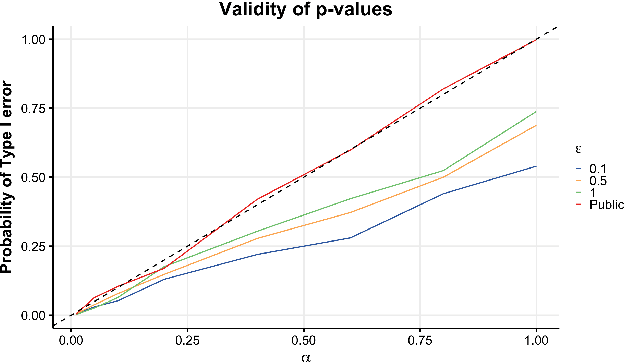
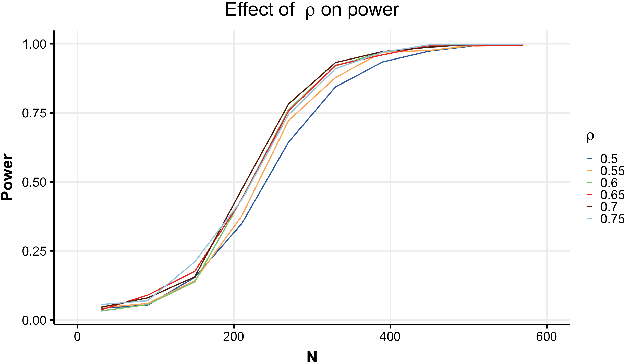
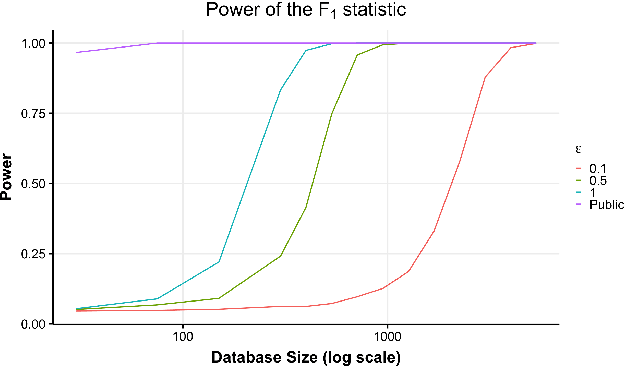
Hypothesis testing is one of the most common types of data analysis and forms the backbone of scientific research in many disciplines. Analysis of variance (ANOVA) in particular is used to detect dependence between a categorical and a numerical variable. Here we show how one can carry out this hypothesis test under the restrictions of differential privacy. We show that the $F$-statistic, the optimal test statistic in the public setting, is no longer optimal in the private setting, and we develop a new test statistic $F_1$ with much higher statistical power. We show how to rigorously compute a reference distribution for the $F_1$ statistic and give an algorithm that outputs accurate $p$-values. We implement our test and experimentally optimize several parameters. We then compare our test to the only previous work on private ANOVA testing, using the same effect size as that work. We see an order of magnitude improvement, with our test requiring only 7% as much data to detect the effect.